q-means: A quantum algorithm for unsupervised machine learning
Paper and Code
Dec 11, 2018


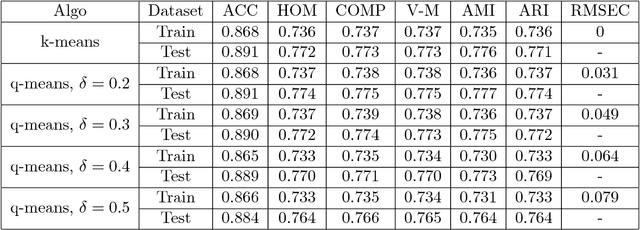
Quantum machine learning is one of the most promising applications of a full-scale quantum computer. Over the past few years, many quantum machine learning algorithms have been proposed that can potentially offer considerable speedups over the corresponding classical algorithms. In this paper, we introduce q-means, a new quantum algorithm for clustering which is a canonical problem in unsupervised machine learning. The $q$-means algorithm has convergence and precision guarantees similar to $k$-means, and it outputs with high probability a good approximation of the $k$ cluster centroids like the classical algorithm. Given a dataset of $N$ $d$-dimensional vectors $v_i$ (seen as a matrix $V \in \mathbb{R}^{N \times d})$ stored in QRAM, the running time of q-means is $\widetilde{O}\left( k d \frac{\eta}{\delta^2}\kappa(V)(\mu(V) + k \frac{\eta}{\delta}) + k^2 \frac{\eta^{1.5}}{\delta^2} \kappa(V)\mu(V) \right)$ per iteration, where $\kappa(V)$ is the condition number, $\mu(V)$ is a parameter that appears in quantum linear algebra procedures and $\eta = \max_{i} ||v_{i}||^{2}$. For a natural notion of well-clusterable datasets, the running time becomes $\widetilde{O}\left( k^2 d \frac{\eta^{2.5}}{\delta^3} + k^{2.5} \frac{\eta^2}{\delta^3} \right)$ per iteration, which is linear in the number of features $d$, and polynomial in the rank $k$, the maximum square norm $\eta$ and the error parameter $\delta$. Both running times are only polylogarithmic in the number of datapoints $N$. Our algorithm provides substantial savings compared to the classical $k$-means algorithm that runs in time $O(kdN)$ per iteration, particularly for the case of large datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge