Quantum Vision Transformers

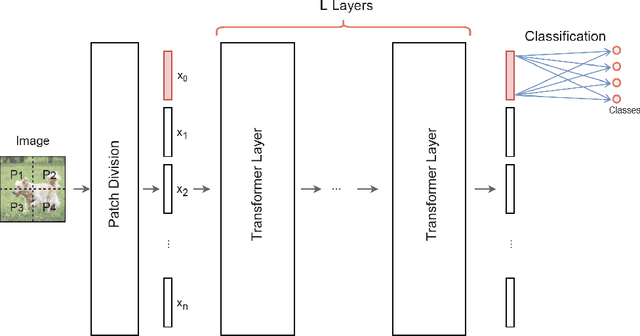
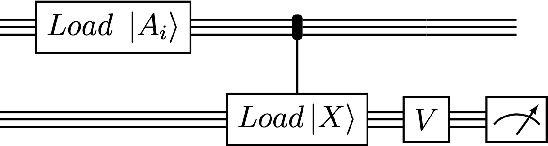
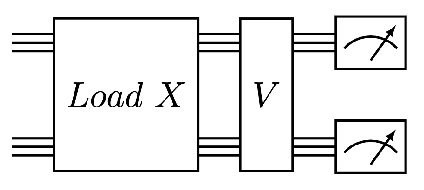
We design and analyse quantum transformers, extending the state-of-the-art classical transformer neural network architectures known to be very performant in natural language processing and image analysis. Building upon the previous work of parametrised quantum circuits for data loading and orthogonal neural layers, we introduce three quantum attention mechanisms, including a quantum transformer based on compound matrices. These quantum architectures can be built using shallow quantum circuits and can provide qualitatively different classification models. We performed extensive simulations of the quantum transformers on standard medical image datasets that showed competitive, and at times better, performance compared with the best classical transformers and other classical benchmarks. The computational complexity of our quantum attention layer proves to be advantageous compared with the classical algorithm with respect to the size of the classified images. Our quantum architectures have thousands of parameters compared with the best classical methods with millions of parameters. Finally, we have implemented our quantum transformers on superconducting quantum computers and obtained encouraging results for up to six qubit experiments.

q-means: A quantum algorithm for unsupervised machine learning

Quantum machine learning is one of the most promising applications of a full-scale quantum computer. Over the past few years, many quantum machine learning algorithms have been proposed that can potentially offer considerable speedups over the corresponding classical algorithms. In this paper, we introduce q-means, a new quantum algorithm for clustering which is a canonical problem in unsupervised machine learning. The $q$-means algorithm has convergence and precision guarantees similar to $k$-means, and it outputs with high probability a good approximation of the $k$ cluster centroids like the classical algorithm. Given a dataset of $N$ $d$-dimensional vectors $v_i$ (seen as a matrix $V \in \mathbb{R}^{N \times d})$ stored in QRAM, the running time of q-means is $\widetilde{O}\left( k d \frac{\eta}{\delta^2}\kappa(V)(\mu(V) + k \frac{\eta}{\delta}) + k^2 \frac{\eta^{1.5}}{\delta^2} \kappa(V)\mu(V) \right)$ per iteration, where $\kappa(V)$ is the condition number, $\mu(V)$ is a parameter that appears in quantum linear algebra procedures and $\eta = \max_{i} ||v_{i}||^{2}$. For a natural notion of well-clusterable datasets, the running time becomes $\widetilde{O}\left( k^2 d \frac{\eta^{2.5}}{\delta^3} + k^{2.5} \frac{\eta^2}{\delta^3} \right)$ per iteration, which is linear in the number of features $d$, and polynomial in the rank $k$, the maximum square norm $\eta$ and the error parameter $\delta$. Both running times are only polylogarithmic in the number of datapoints $N$. Our algorithm provides substantial savings compared to the classical $k$-means algorithm that runs in time $O(kdN)$ per iteration, particularly for the case of large datasets.