Quantum Reinforcement Learning via Policy Iteration

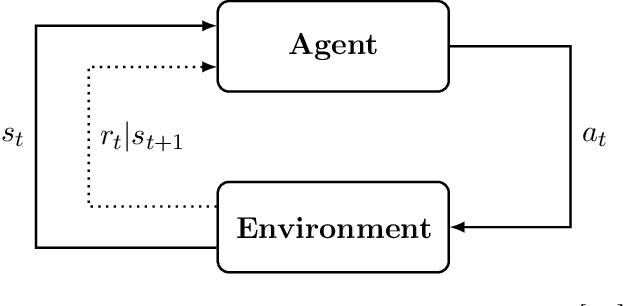
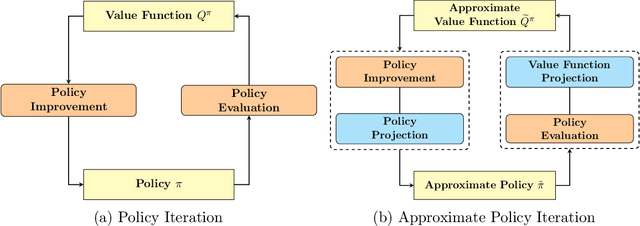
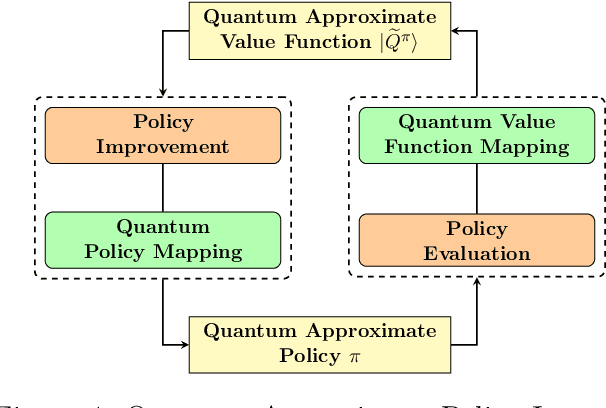
Quantum computing has shown the potential to substantially speed up machine learning applications, in particular for supervised and unsupervised learning. Reinforcement learning, on the other hand, has become essential for solving many decision making problems and policy iteration methods remain the foundation of such approaches. In this paper, we provide a general framework for performing quantum reinforcement learning via policy iteration. We validate our framework by designing and analyzing: \emph{quantum policy evaluation} methods for infinite horizon discounted problems by building quantum states that approximately encode the value function of a policy $\pi$; and \emph{quantum policy improvement} methods by post-processing measurement outcomes on these quantum states. Last, we study the theoretical and experimental performance of our quantum algorithms on two environments from OpenAI's Gym.

Quantum algorithms for Second-Order Cone Programming and Support Vector Machines

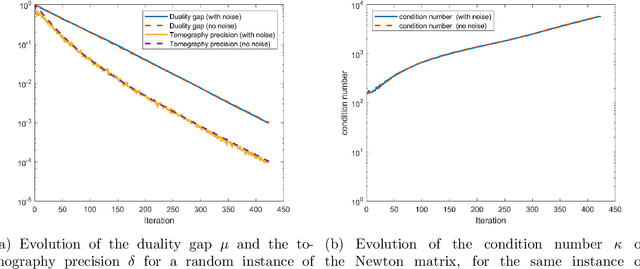
Second order cone programs (SOCPs) are a class of structured convex optimization problems that generalize linear programs. We present a quantum algorithm for SOCPs based on a quantum variant of the interior point method. Our algorithm outputs a classical solution to the SOCP with objective value $\epsilon$ close to the optimal in time $\widetilde{O} \left( n\sqrt{r} \frac{\zeta \kappa}{\delta^2} \log \left(1/\epsilon\right) \right)$ where $r$ is the rank and $n$ the dimension of the SOCP, $\delta$ bounds the distance from strict feasibility for the intermediate solutions, $\zeta$ is a parameter bounded by $\sqrt{n}$, and $\kappa$ is an upper bound on the condition number of matrices arising in the classical interior point method for SOCPs. We present applications to the support vector machine (SVM) problem in machine learning that reduces to SOCPs. We provide experimental evidence that the quantum algorithm achieves an asymptotic speedup over classical SVM algorithms with a running time $\widetilde{O}(n^{2.557})$ for random SVM instances. The best known classical algorithms for such instances have complexity $\widetilde{O} \left( n^{\omega+0.5}\log(1/\epsilon) \right)$, where $\omega$ is the matrix multiplication exponent that has a theoretical value of around $2.373$, but is closer to $3$ in practice.

Quantum Expectation-Maximization for Gaussian Mixture Models

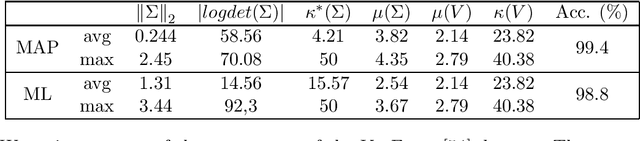
The Expectation-Maximization (EM) algorithm is a fundamental tool in unsupervised machine learning. It is often used as an efficient way to solve Maximum Likelihood (ML) estimation problems, especially for models with latent variables. It is also the algorithm of choice to fit mixture models: generative models that represent unlabelled points originating from $k$ different processes, as samples from $k$ multivariate distributions. In this work we define and use a quantum version of EM to fit a Gaussian Mixture Model. Given quantum access to a dataset of $n$ vectors of dimension $d$, our algorithm has convergence and precision guarantees similar to the classical algorithm, but the runtime is only polylogarithmic in the number of elements in the training set, and is polynomial in other parameters - as the dimension of the feature space, and the number of components in the mixture. We generalize further the algorithm in two directions. First, we show how to fit any mixture model of probability distributions in the exponential family. Then, we show how to use this algorithm to compute the Maximum a Posteriori (MAP) estimate of a mixture model: the Bayesian approach to likelihood estimation problems. We discuss the performance of the algorithm on datasets that are expected to be classified successfully by those algorithms, arguing that on those cases we can give strong guarantees on the runtime.

q-means: A quantum algorithm for unsupervised machine learning

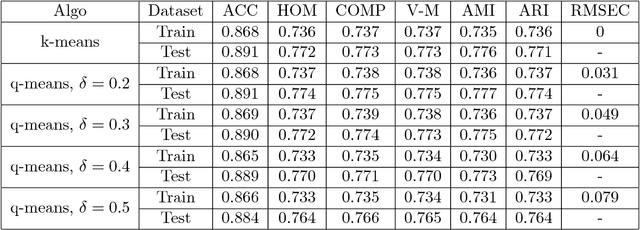
Quantum machine learning is one of the most promising applications of a full-scale quantum computer. Over the past few years, many quantum machine learning algorithms have been proposed that can potentially offer considerable speedups over the corresponding classical algorithms. In this paper, we introduce q-means, a new quantum algorithm for clustering which is a canonical problem in unsupervised machine learning. The $q$-means algorithm has convergence and precision guarantees similar to $k$-means, and it outputs with high probability a good approximation of the $k$ cluster centroids like the classical algorithm. Given a dataset of $N$ $d$-dimensional vectors $v_i$ (seen as a matrix $V \in \mathbb{R}^{N \times d})$ stored in QRAM, the running time of q-means is $\widetilde{O}\left( k d \frac{\eta}{\delta^2}\kappa(V)(\mu(V) + k \frac{\eta}{\delta}) + k^2 \frac{\eta^{1.5}}{\delta^2} \kappa(V)\mu(V) \right)$ per iteration, where $\kappa(V)$ is the condition number, $\mu(V)$ is a parameter that appears in quantum linear algebra procedures and $\eta = \max_{i} ||v_{i}||^{2}$. For a natural notion of well-clusterable datasets, the running time becomes $\widetilde{O}\left( k^2 d \frac{\eta^{2.5}}{\delta^3} + k^{2.5} \frac{\eta^2}{\delta^3} \right)$ per iteration, which is linear in the number of features $d$, and polynomial in the rank $k$, the maximum square norm $\eta$ and the error parameter $\delta$. Both running times are only polylogarithmic in the number of datapoints $N$. Our algorithm provides substantial savings compared to the classical $k$-means algorithm that runs in time $O(kdN)$ per iteration, particularly for the case of large datasets.