Quantum algorithms for Second-Order Cone Programming and Support Vector Machines
Paper and Code
Aug 23, 2019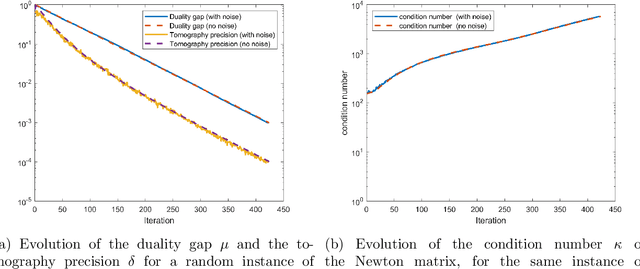


Second order cone programs (SOCPs) are a class of structured convex optimization problems that generalize linear programs. We present a quantum algorithm for SOCPs based on a quantum variant of the interior point method. Our algorithm outputs a classical solution to the SOCP with objective value $\epsilon$ close to the optimal in time $\widetilde{O} \left( n\sqrt{r} \frac{\zeta \kappa}{\delta^2} \log \left(1/\epsilon\right) \right)$ where $r$ is the rank and $n$ the dimension of the SOCP, $\delta$ bounds the distance from strict feasibility for the intermediate solutions, $\zeta$ is a parameter bounded by $\sqrt{n}$, and $\kappa$ is an upper bound on the condition number of matrices arising in the classical interior point method for SOCPs. We present applications to the support vector machine (SVM) problem in machine learning that reduces to SOCPs. We provide experimental evidence that the quantum algorithm achieves an asymptotic speedup over classical SVM algorithms with a running time $\widetilde{O}(n^{2.557})$ for random SVM instances. The best known classical algorithms for such instances have complexity $\widetilde{O} \left( n^{\omega+0.5}\log(1/\epsilon) \right)$, where $\omega$ is the matrix multiplication exponent that has a theoretical value of around $2.373$, but is closer to $3$ in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge