Quantum Reinforcement Learning via Policy Iteration

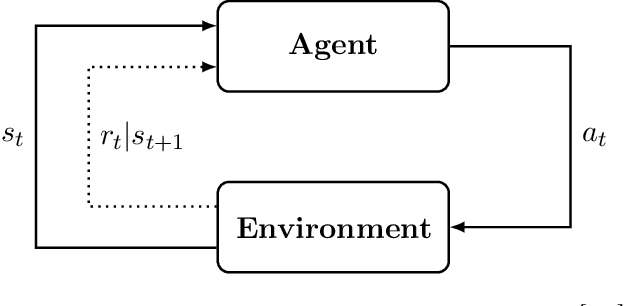
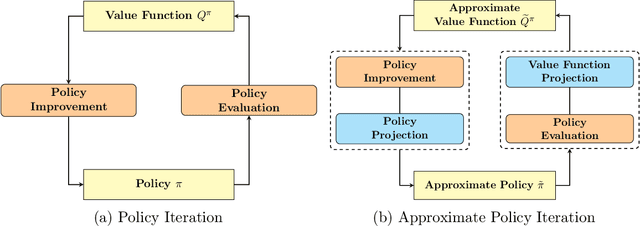
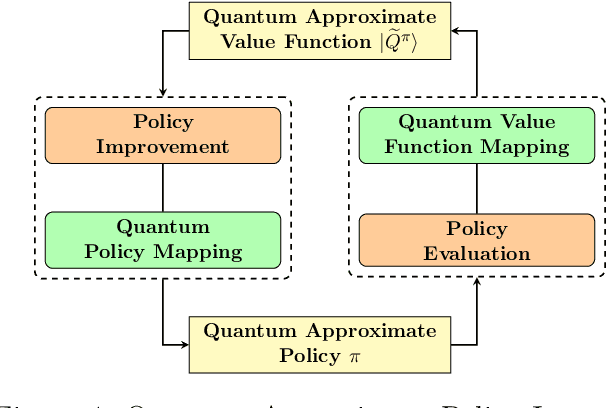
Quantum computing has shown the potential to substantially speed up machine learning applications, in particular for supervised and unsupervised learning. Reinforcement learning, on the other hand, has become essential for solving many decision making problems and policy iteration methods remain the foundation of such approaches. In this paper, we provide a general framework for performing quantum reinforcement learning via policy iteration. We validate our framework by designing and analyzing: \emph{quantum policy evaluation} methods for infinite horizon discounted problems by building quantum states that approximately encode the value function of a policy $\pi$; and \emph{quantum policy improvement} methods by post-processing measurement outcomes on these quantum states. Last, we study the theoretical and experimental performance of our quantum algorithms on two environments from OpenAI's Gym.