Scalable On-Hardware Training of Quantum Neural Networks and Application to Clinical Data Imputation

Training quantum neural networks (QNNs) on quantum hardware is currently bottlenecked by the cost of gradient estimation: standard parameter-shift methods require a number of circuit evaluations that grows quadratically with the number of trainable parameters, making hardware-based optimisation impractical beyond small system sizes. In this work, we introduce a training framework that reduces this cost to logarithmic in the number of qubits, making gradient-based QNN optimisation feasible on near-term hardware at increasing scales. Our framework combines three co-designed ingredients: (i) a structured, subspace-preserving Butterfly circuit architecture with $O(n \log n)$ parameters and logarithmic depth; (ii) a layer-wise training strategy that confines on-hardware optimisation to one small, well-structured layer at a time; and (iii) a parallelised parameter-shift rule that exploits the commuting structure within each Butterfly layer to extract all gradients in a constant number of circuit executions. Together these reduce the number of distinct circuit evaluations per optimisation step from $O(n^2)$ to $O(\log n)$. We validate the framework on clinical data imputation using the MIMIC-III electronic health record dataset, a demanding benchmark sensitive to optimisation instability and model variance. Hybrid classical-quantum models are trained directly on IonQ Forte Enterprise trapped-ion hardware at 16 qubits without performance degradation relative to ideal or noisy simulation and via tensor-network simulation at 32 qubits, with 32-qubit inference executed on hardware. The resulting models match or exceed strong classical neural baselines in downstream patient survival prediction while exhibiting reduced variance across runs, demonstrating that the proposed framework enables practical, scalable QNN training under realistic hardware constraints.

Unsupervised Physics-Informed Operator Learning through Multi-Stage Curriculum Training

Solving partial differential equations remains a central challenge in scientific machine learning. Neural operators offer a promising route by learning mappings between function spaces and enabling resolution-independent inference, yet they typically require supervised data. Physics-informed neural networks address this limitation through unsupervised training with physical constraints but often suffer from unstable convergence and limited generalization capability. To overcome these issues, we introduce a multi-stage physics-informed training strategy that achieves convergence by progressively enforcing boundary conditions in the loss landscape and subsequently incorporating interior residuals. At each stage the optimizer is re-initialized, acting as a continuation mechanism that restores stability and prevents gradient stagnation. We further propose the Physics-Informed Spline Fourier Neural Operator (PhIS-FNO), combining Fourier layers with Hermite spline kernels for smooth residual evaluation. Across canonical benchmarks, PhIS-FNO attains a level of accuracy comparable to that of supervised learning, using labeled information only along a narrow boundary region, establishing staged, spline-based optimization as a robust paradigm for physics-informed operator learning.

Bayesian Quantum Orthogonal Neural Networks for Anomaly Detection

Identification of defects or anomalies in 3D objects is a crucial task to ensure correct functionality. In this work, we combine Bayesian learning with recent developments in quantum and quantum-inspired machine learning, specifically orthogonal neural networks, to tackle this anomaly detection problem for an industrially relevant use case. Bayesian learning enables uncertainty quantification of predictions, while orthogonality in weight matrices enables smooth training. We develop orthogonal (quantum) versions of 3D convolutional neural networks and show that these models can successfully detect anomalies in 3D objects. To test the feasibility of incorporating quantum computers into a quantum-enhanced anomaly detection pipeline, we perform hardware experiments with our models on IBM's 127-qubit Brisbane device, testing the effect of noise and limited measurement shots.

Training-efficient density quantum machine learning

Quantum machine learning requires powerful, flexible and efficiently trainable models to be successful in solving challenging problems. In this work, we present density quantum neural networks, a learning model incorporating randomisation over a set of trainable unitaries. These models generalise quantum neural networks using parameterised quantum circuits, and allow a trade-off between expressibility and efficient trainability, particularly on quantum hardware. We demonstrate the flexibility of the formalism by applying it to two recently proposed model families. The first are commuting-block quantum neural networks (QNNs) which are efficiently trainable but may be limited in expressibility. The second are orthogonal (Hamming-weight preserving) quantum neural networks which provide well-defined and interpretable transformations on data but are challenging to train at scale on quantum devices. Density commuting QNNs improve capacity with minimal gradient complexity overhead, and density orthogonal neural networks admit a quadratic-to-constant gradient query advantage with minimal to no performance loss. We conduct numerical experiments on synthetic translationally invariant data and MNIST image data with hyperparameter optimisation to support our findings. Finally, we discuss the connection to post-variational quantum neural networks, measurement-based quantum machine learning and the dropout mechanism.

Quantum Vision Transformers

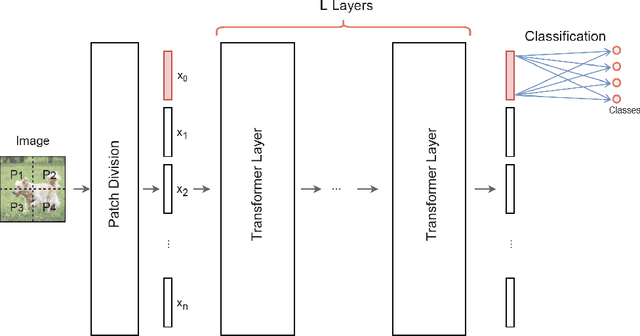
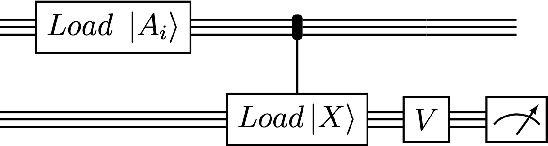
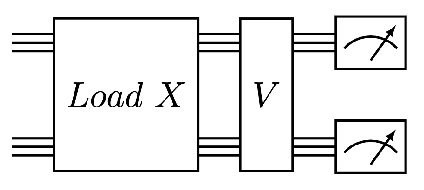
We design and analyse quantum transformers, extending the state-of-the-art classical transformer neural network architectures known to be very performant in natural language processing and image analysis. Building upon the previous work of parametrised quantum circuits for data loading and orthogonal neural layers, we introduce three quantum attention mechanisms, including a quantum transformer based on compound matrices. These quantum architectures can be built using shallow quantum circuits and can provide qualitatively different classification models. We performed extensive simulations of the quantum transformers on standard medical image datasets that showed competitive, and at times better, performance compared with the best classical transformers and other classical benchmarks. The computational complexity of our quantum attention layer proves to be advantageous compared with the classical algorithm with respect to the size of the classified images. Our quantum architectures have thousands of parameters compared with the best classical methods with millions of parameters. Finally, we have implemented our quantum transformers on superconducting quantum computers and obtained encouraging results for up to six qubit experiments.