Reconquering Bell sampling on qudits: stabilizer learning and testing, quantum pseudorandomness bounds, and more

Bell sampling is a simple yet powerful tool based on measuring two copies of a quantum state in the Bell basis, and has found applications in a plethora of problems related to stabiliser states and measures of magic. However, it was not known how to generalise the procedure from qubits to $d$-level systems -- qudits -- for all dimensions $d > 2$ in a useful way. Indeed, a prior work of the authors (arXiv'24) showed that the natural extension of Bell sampling to arbitrary dimensions fails to provide meaningful information about the quantum states being measured. In this paper, we overcome the difficulties encountered in previous works and develop a useful generalisation of Bell sampling to qudits of all $d\geq 2$. At the heart of our primitive is a new unitary, based on Lagrange's four-square theorem, that maps four copies of any stabiliser state $|\mathcal{S}\rangle$ to four copies of its complex conjugate $|\mathcal{S}^\ast\rangle$ (up to some Pauli operator), which may be of independent interest. We then demonstrate the utility of our new Bell sampling technique by lifting several known results from qubits to qudits for any $d\geq 2$: 1. Learning stabiliser states in $O(n^3)$ time with $O(n)$ samples; 2. Solving the Hidden Stabiliser Group Problem in $\tilde{O}(n^3/\varepsilon)$ time with $\tilde{O}(n/\varepsilon)$ samples; 3. Testing whether $|\psi\rangle$ has stabiliser size at least $d^t$ or is $\varepsilon$-far from all such states in $\tilde{O}(n^3/\varepsilon)$ time with $\tilde{O}(n/\varepsilon)$ samples; 4. Clifford circuits with at most $n/2$ single-qudit non-Clifford gates cannot prepare pseudorandom states; 5. Testing whether $|\psi\rangle$ has stabiliser fidelity at least $1-\varepsilon_1$ or at most $1-\varepsilon_2$ with $O(d^2/\varepsilon_2)$ samples if $\varepsilon_1 = 0$ or $O(d^2/\varepsilon_2^2)$ samples if $\varepsilon_1 = O(d^{-2})$.

Quantum algorithm for training nonlinear SVMs in almost linear time

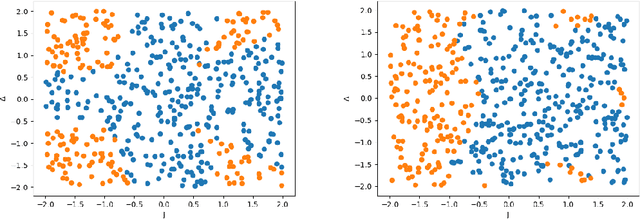
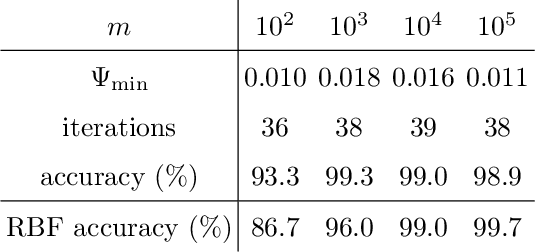
We propose a quantum algorithm for training nonlinear support vector machines (SVM) for feature space learning where classical input data is encoded in the amplitudes of quantum states. Based on the classical algorithm of Joachims, our algorithm has a running time which scales linearly in the number of training examples (up to polylogarithmic factors) and applies to the standard soft-margin $\ell_1$-SVM model. In contrast, the best classical algorithms have super-linear scaling for general feature maps, and achieve linear $m$ scaling only for linear SVMs, where classification is performed in the original input data space, or for the special case of feature maps corresponding to shift-invariant kernels. Similarly, previously proposed quantum algorithms either have super-linear scaling in $m$, or else apply to different SVM models such as the hard-margin or least squares $\ell_2$-SVM, which lack certain desirable properties of the soft-margin $\ell_1$-SVM model. We classically simulate our algorithm and give evidence that it can perform well in practice, and not only for asymptotically large data sets.

Quantum algorithms for feedforward neural networks

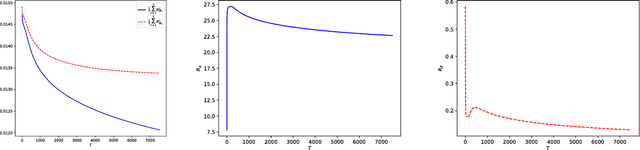
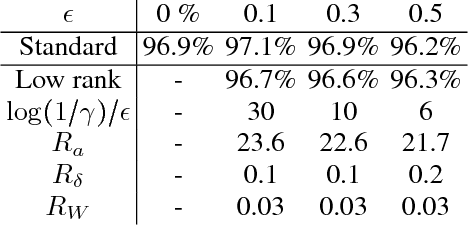
Quantum machine learning has the potential for broad industrial applications, and the development of quantum algorithms for improving the performance of neural networks is of particular interest given the central role they play in machine learning today. In this paper we present quantum algorithms for training and evaluating feedforward neural networks based on the canonical classical feedforward and backpropagation algorithms. Our algorithms rely on an efficient quantum subroutine for approximating the inner products between vectors, and on storing intermediate values in quantum random access memory for fast retrieval at later stages. The running times of our algorithms can be quadratically faster than their classical counterparts, since they depend linearly on the number of neurons in the network, as opposed to the number of edges as in the classical case. This makes our algorithms suited for large-scale, highly-connected networks where the number of edges in the network dominates the classical algorithmic running time.