Quantum algorithm for training nonlinear SVMs in almost linear time

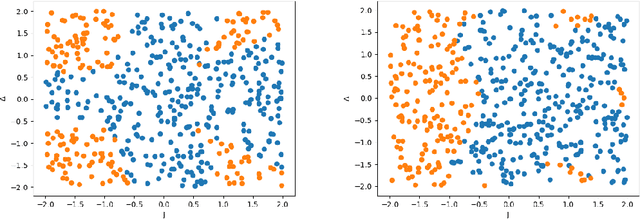
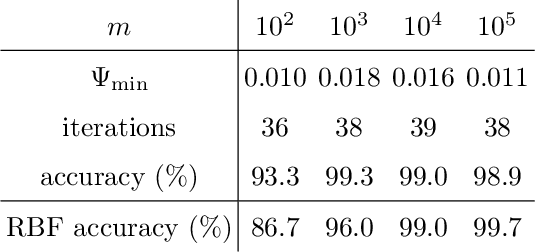
We propose a quantum algorithm for training nonlinear support vector machines (SVM) for feature space learning where classical input data is encoded in the amplitudes of quantum states. Based on the classical algorithm of Joachims, our algorithm has a running time which scales linearly in the number of training examples (up to polylogarithmic factors) and applies to the standard soft-margin $\ell_1$-SVM model. In contrast, the best classical algorithms have super-linear scaling for general feature maps, and achieve linear $m$ scaling only for linear SVMs, where classification is performed in the original input data space, or for the special case of feature maps corresponding to shift-invariant kernels. Similarly, previously proposed quantum algorithms either have super-linear scaling in $m$, or else apply to different SVM models such as the hard-margin or least squares $\ell_2$-SVM, which lack certain desirable properties of the soft-margin $\ell_1$-SVM model. We classically simulate our algorithm and give evidence that it can perform well in practice, and not only for asymptotically large data sets.