Quantum classification of the MNIST dataset via Slow Feature Analysis
Paper and Code
Jun 12, 2018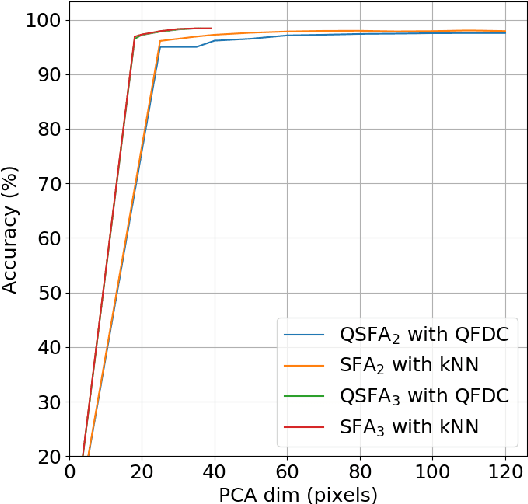
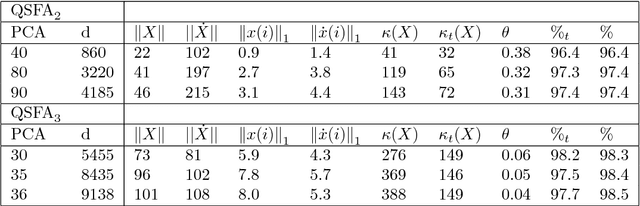
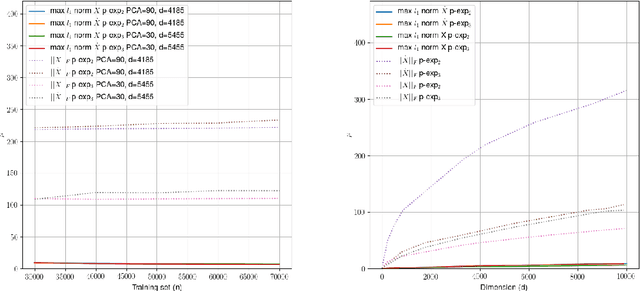
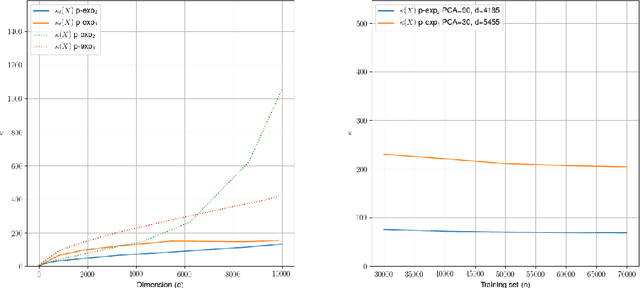
Quantum machine learning carries the promise to revolutionize information and communication technologies. While a number of quantum algorithms with potential exponential speedups have been proposed already, it is quite difficult to provide convincing evidence that quantum computers with quantum memories will be in fact useful to solve real-world problems. Our work makes considerable progress towards this goal. We design quantum techniques for Dimensionality Reduction and for Classification, and combine them to provide an efficient and high accuracy quantum classifier that we test on the MNIST dataset. More precisely, we propose a quantum version of Slow Feature Analysis (QSFA), a dimensionality reduction technique that maps the dataset in a lower dimensional space where we can apply a novel quantum classification procedure, the Quantum Frobenius Distance (QFD). We simulate the quantum classifier (including errors) and show that it can provide classification of the MNIST handwritten digit dataset, a widely used dataset for benchmarking classification algorithms, with $98.5\%$ accuracy, similar to the classical case. The running time of the quantum classifier is polylogarithmic in the dimension and number of data points. We also provide evidence that the other parameters on which the running time depends (condition number, Frobenius norm, error threshold, etc.) scale favorably in practice, thus ascertaining the efficiency of our algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge