Agnostic Process Tomography

Characterizing a quantum system by learning its state or evolution is a fundamental problem in quantum physics and learning theory with a myriad of applications. Recently, as a new approach to this problem, the task of agnostic state tomography was defined, in which one aims to approximate an arbitrary quantum state by a simpler one in a given class. Generalizing this notion to quantum processes, we initiate the study of agnostic process tomography: given query access to an unknown quantum channel $\Phi$ and a known concept class $\mathcal{C}$ of channels, output a quantum channel that approximates $\Phi$ as well as any channel in the concept class $\mathcal{C}$, up to some error. In this work, we propose several natural applications for this new task in quantum machine learning, quantum metrology, classical simulation, and error mitigation. In addition, we give efficient agnostic process tomography algorithms for a wide variety of concept classes, including Pauli strings, Pauli channels, quantum junta channels, low-degree channels, and a class of channels produced by $\mathsf{QAC}^0$ circuits. The main technical tool we use is Pauli spectrum analysis of operators and superoperators. We also prove that, using ancilla qubits, any agnostic state tomography algorithm can be extended to one solving agnostic process tomography for a compatible concept class of unitaries, immediately giving us efficient agnostic learning algorithms for Clifford circuits, Clifford circuits with few T gates, and circuits consisting of a tensor product of single-qubit gates. Together, our results provide insight into the conditions and new algorithms necessary to extend the learnability of a concept class from the standard tomographic setting to the agnostic one.

Noise-tolerant learnability of shallow quantum circuits from statistics and the cost of quantum pseudorandomness

This work studies the learnability of unknown quantum circuits in the near term. We prove the natural robustness of quantum statistical queries for learning quantum processes and provide an efficient way to benchmark various classes of noise from statistics, which gives us a powerful framework for developing noise-tolerant algorithms. We adapt a learning algorithm for constant-depth quantum circuits to the quantum statistical query setting with a small overhead in the query complexity. We prove average-case lower bounds for learning random quantum circuits of logarithmic and higher depths within diamond distance with statistical queries. Additionally, we show the hardness of the quantum threshold search problem from quantum statistical queries and discuss its implications for the learnability of shallow quantum circuits. Finally, we prove that pseudorandom unitaries (PRUs) cannot be constructed using circuits of constant depth by constructing an efficient distinguisher and proving a new variation of the quantum no-free lunch theorem.

Learning Quantum Processes with Quantum Statistical Queries

Learning complex quantum processes is a central challenge in many areas of quantum computing and quantum machine learning, with applications in quantum benchmarking, cryptanalysis, and variational quantum algorithms. This paper introduces the first learning framework for studying quantum process learning within the Quantum Statistical Query (QSQ) model, providing the first formal definition of statistical queries to quantum processes (QPSQs). The framework allows us to propose an efficient QPSQ learner for arbitrary quantum processes accompanied by a provable performance guarantee. We also provide numerical simulations to demonstrate the efficacy of this algorithm. The practical relevance of this framework is exemplified through application in cryptanalysis, highlighting vulnerabilities of Classical-Readout Quantum Physical Unclonable Functions (CR-QPUFs), addressing an important open question in the field of quantum hardware security. This work marks a significant step towards understanding the learnability of quantum processes and shedding light on their security implications.

A unifying framework for differentially private quantum algorithms

Differential privacy is a widely used notion of security that enables the processing of sensitive information. In short, differentially private algorithms map "neighbouring" inputs to close output distributions. Prior work proposed several quantum extensions of differential privacy, each of them built on substantially different notions of neighbouring quantum states. In this paper, we propose a novel and general definition of neighbouring quantum states. We demonstrate that this definition captures the underlying structure of quantum encodings and can be used to provide exponentially tighter privacy guarantees for quantum measurements. Our approach combines the addition of classical and quantum noise and is motivated by the noisy nature of near-term quantum devices. Moreover, we also investigate an alternative setting where we are provided with multiple copies of the input state. In this case, differential privacy can be ensured with little loss in accuracy combining concentration of measure and noise-adding mechanisms. En route, we prove the advanced joint convexity of the quantum hockey-stick divergence and we demonstrate how this result can be applied to quantum differential privacy. Finally, we complement our theoretical findings with an empirical estimation of the certified adversarial robustness ensured by differentially private measurements.

Unclonability and Quantum Cryptanalysis: From Foundations to Applications

The impossibility of creating perfect identical copies of unknown quantum systems is a fundamental concept in quantum theory and one of the main non-classical properties of quantum information. This limitation imposed by quantum mechanics, famously known as the no-cloning theorem, has played a central role in quantum cryptography as a key component in the security of quantum protocols. In this thesis, we look at Unclonability in a broader context in physics and computer science and more specifically through the lens of cryptography, learnability and hardware assumptions. We introduce new notions of unclonability in the quantum world, namely quantum physical unclonability, and study the relationship with cryptographic properties and assumptions such as unforgeability, and quantum pseudorandomness. The purpose of this study is to bring new insights into the field of quantum cryptanalysis and into the notion of unclonability itself. We also discuss several applications of this new type of unclonability as a cryptographic resource for designing provably secure quantum protocols. Furthermore, we present a new practical cryptanalysis technique concerning the problem of approximate cloning of quantum states. We design a quantum machine learning-based cryptanalysis algorithm to demonstrate the power of quantum learning tools as both attack strategies and powerful tools for the practical study of quantum unclonability.

Differential Privacy Amplification in Quantum and Quantum-inspired Algorithms

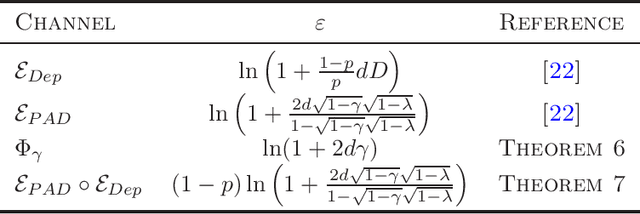
Differential privacy provides a theoretical framework for processing a dataset about $n$ users, in a way that the output reveals a minimal information about any single user. Such notion of privacy is usually ensured by noise-adding mechanisms and amplified by several processes, including subsampling, shuffling, iteration, mixing and diffusion. In this work, we provide privacy amplification bounds for quantum and quantum-inspired algorithms. In particular, we show for the first time, that algorithms running on quantum encoding of a classical dataset or the outcomes of quantum-inspired classical sampling, amplify differential privacy. Moreover, we prove that a quantum version of differential privacy is amplified by the composition of quantum channels, provided that they satisfy some mixing conditions.

Variational Quantum Cloning: Improving Practicality for Quantum Cryptanalysis

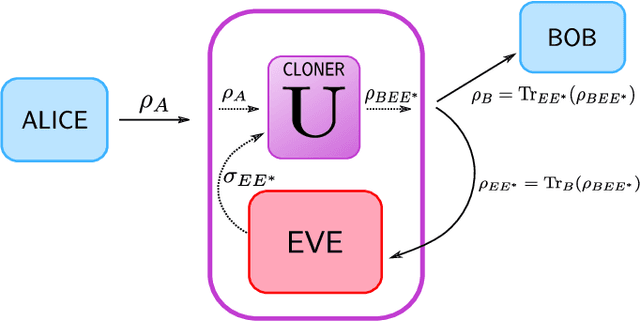
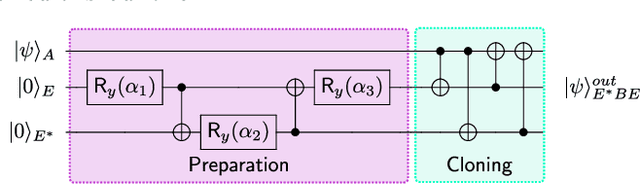
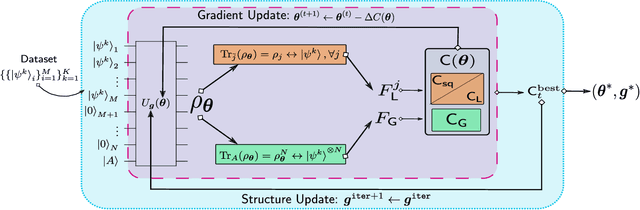
Cryptanalysis on standard quantum cryptographic systems generally involves finding optimal adversarial attack strategies on the underlying protocols. The core principle of modelling quantum attacks in many cases reduces to the adversary's ability to clone unknown quantum states which facilitates the extraction of some meaningful secret information. Explicit optimal attack strategies typically require high computational resources due to large circuit depths or, in many cases, are unknown. In this work, we propose variational quantum cloning (VQC), a quantum machine learning based cryptanalysis algorithm which allows an adversary to obtain optimal (approximate) cloning strategies with short depth quantum circuits, trained using hybrid classical-quantum techniques. The algorithm contains operationally meaningful cost functions with theoretical guarantees, quantum circuit structure learning and gradient descent based optimisation. Our approach enables the end-to-end discovery of hardware efficient quantum circuits to clone specific families of quantum states, which in turn leads to an improvement in cloning fidelites when implemented on quantum hardware: the Rigetti Aspen chip. Finally, we connect these results to quantum cryptographic primitives, in particular quantum coin flipping. We derive attacks on two protocols as examples, based on quantum cloning and facilitated by VQC. As a result, our algorithm can improve near term attacks on these protocols, using approximate quantum cloning as a resource.