FastUMI-100K: Advancing Data-driven Robotic Manipulation with a Large-scale UMI-style Dataset

Data-driven robotic manipulation learning depends on large-scale, high-quality expert demonstration datasets. However, existing datasets, which primarily rely on human teleoperated robot collection, are limited in terms of scalability, trajectory smoothness, and applicability across different robotic embodiments in real-world environments. In this paper, we present FastUMI-100K, a large-scale UMI-style multimodal demonstration dataset, designed to overcome these limitations and meet the growing complexity of real-world manipulation tasks. Collected by FastUMI, a novel robotic system featuring a modular, hardware-decoupled mechanical design and an integrated lightweight tracking system, FastUMI-100K offers a more scalable, flexible, and adaptable solution to fulfill the diverse requirements of real-world robot demonstration data. Specifically, FastUMI-100K contains over 100K+ demonstration trajectories collected across representative household environments, covering 54 tasks and hundreds of object types. Our dataset integrates multimodal streams, including end-effector states, multi-view wrist-mounted fisheye images and textual annotations. Each trajectory has a length ranging from 120 to 500 frames. Experimental results demonstrate that FastUMI-100K enables high policy success rates across various baseline algorithms, confirming its robustness, adaptability, and real-world applicability for solving complex, dynamic manipulation challenges. The source code and dataset will be released in this link https://github.com/MrKeee/FastUMI-100K.

Direct Fisher Score Estimation for Likelihood Maximization

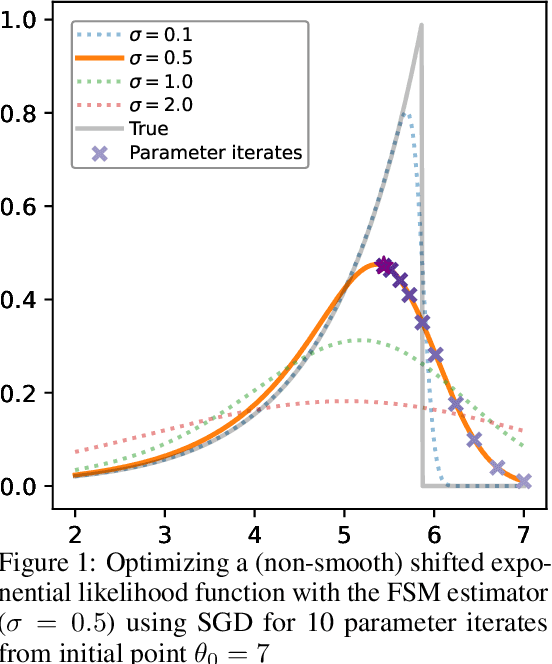
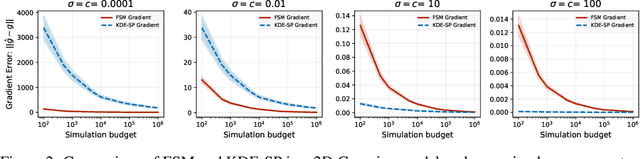
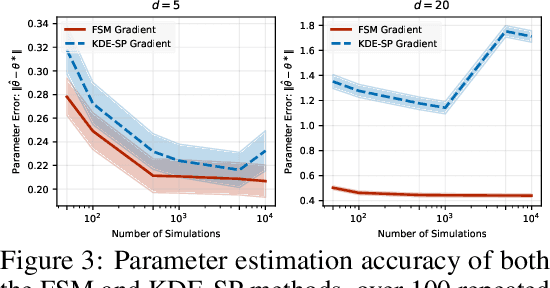
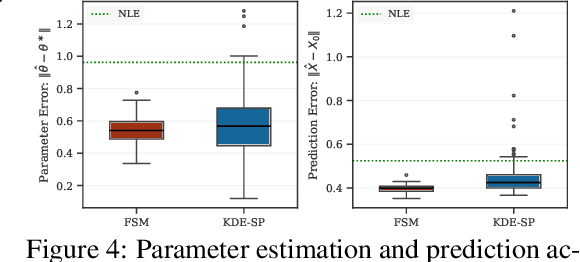
We study the problem of likelihood maximization when the likelihood function is intractable but model simulations are readily available. We propose a sequential, gradient-based optimization method that directly models the Fisher score based on a local score matching technique which uses simulations from a localized region around each parameter iterate. By employing a linear parameterization to the surrogate score model, our technique admits a closed-form, least-squares solution. This approach yields a fast, flexible, and efficient approximation to the Fisher score, effectively smoothing the likelihood objective and mitigating the challenges posed by complex likelihood landscapes. We provide theoretical guarantees for our score estimator, including bounds on the bias introduced by the smoothing. Empirical results on a range of synthetic and real-world problems demonstrate the superior performance of our method compared to existing benchmarks.

Missing Data Imputation by Reducing Mutual Information with Rectified Flows

This paper introduces a novel iterative method for missing data imputation that sequentially reduces the mutual information between data and their corresponding missing mask. Inspired by GAN-based approaches, which train generators to decrease the predictability of missingness patterns, our method explicitly targets the reduction of mutual information. Specifically, our algorithm iteratively minimizes the KL divergence between the joint distribution of the imputed data and missing mask, and the product of their marginals from the previous iteration. We show that the optimal imputation under this framework corresponds to solving an ODE, whose velocity field minimizes a rectified flow training objective. We further illustrate that some existing imputation techniques can be interpreted as approximate special cases of our mutual-information-reducing framework. Comprehensive experiments on synthetic and real-world datasets validate the efficacy of our proposed approach, demonstrating superior imputation performance.

Every FLOP Counts: Scaling a 300B Mixture-of-Experts LING LLM without Premium GPUs

In this technical report, we tackle the challenges of training large-scale Mixture of Experts (MoE) models, focusing on overcoming cost inefficiency and resource limitations prevalent in such systems. To address these issues, we present two differently sized MoE large language models (LLMs), namely Ling-Lite and Ling-Plus (referred to as "Bailing" in Chinese, spelled B\v{a}il\'ing in Pinyin). Ling-Lite contains 16.8 billion parameters with 2.75 billion activated parameters, while Ling-Plus boasts 290 billion parameters with 28.8 billion activated parameters. Both models exhibit comparable performance to leading industry benchmarks. This report offers actionable insights to improve the efficiency and accessibility of AI development in resource-constrained settings, promoting more scalable and sustainable technologies. Specifically, to reduce training costs for large-scale MoE models, we propose innovative methods for (1) optimization of model architecture and training processes, (2) refinement of training anomaly handling, and (3) enhancement of model evaluation efficiency. Additionally, leveraging high-quality data generated from knowledge graphs, our models demonstrate superior capabilities in tool use compared to other models. Ultimately, our experimental findings demonstrate that a 300B MoE LLM can be effectively trained on lower-performance devices while achieving comparable performance to models of a similar scale, including dense and MoE models. Compared to high-performance devices, utilizing a lower-specification hardware system during the pre-training phase demonstrates significant cost savings, reducing computing costs by approximately 20%. The models can be accessed at https://huggingface.co/inclusionAI.

Guiding Time-Varying Generative Models with Natural Gradients on Exponential Family Manifold

Optimising probabilistic models is a well-studied field in statistics. However, its connection with the training of generative models remains largely under-explored. In this paper, we show that the evolution of time-varying generative models can be projected onto an exponential family manifold, naturally creating a link between the parameters of a generative model and those of a probabilistic model. We then train the generative model by moving its projection on the manifold according to the natural gradient descent scheme. This approach also allows us to approximate the natural gradient of the KL divergence efficiently without relying on MCMC for intractable models. Furthermore, we propose particle versions of the algorithm, which feature closed-form update rules for any parametric model within the exponential family. Through toy and real-world experiments, we validate the effectiveness of the proposed algorithms.

Machine Learning Based Probe Skew Correction for High-frequency BH Loop Measurements

Experimental characterization of magnetic components has grown to be increasingly important to understand and model their behaviours in high-frequency PWM converters. The BH loop measurement is the only available approach to separate the core loss as an electrical method, which, however, is suspective to the probe phase skew. As an alternative to the regular de-skew approaches based on hardware, this work proposes a novel machine-learning-based method to identify and correct the probe skew, which builds on the newly discovered correlation between the skew and the shape/trajectory of the measured BH loop. A special technique is proposed to artificially generate the skewed images from measured waveforms as augmented training sets. A machine learning pipeline is developed with the Convolutional Neural Network (CNN) to treat the problem as an image-based prediction task. The trained model has demonstrated a high accuracy in identifying the skew value from a BH loop unseen by the model, which enables the compensation of the skew to yield the corrected core loss value and BH loop.

A Light-Weight Framework for Open-Set Object Detection with Decoupled Feature Alignment in Joint Space

Open-set object detection (OSOD) is highly desirable for robotic manipulation in unstructured environments. However, existing OSOD methods often fail to meet the requirements of robotic applications due to their high computational burden and complex deployment. To address this issue, this paper proposes a light-weight framework called Decoupled OSOD (DOSOD), which is a practical and highly efficient solution to support real-time OSOD tasks in robotic systems. Specifically, DOSOD builds upon the YOLO-World pipeline by integrating a vision-language model (VLM) with a detector. A Multilayer Perceptron (MLP) adaptor is developed to transform text embeddings extracted by the VLM into a joint space, within which the detector learns the region representations of class-agnostic proposals. Cross-modality features are directly aligned in the joint space, avoiding the complex feature interactions and thereby improving computational efficiency. DOSOD operates like a traditional closed-set detector during the testing phase, effectively bridging the gap between closed-set and open-set detection. Compared to the baseline YOLO-World, the proposed DOSOD significantly enhances real-time performance while maintaining comparable accuracy. The slight DOSOD-S model achieves a Fixed AP of $26.7\%$, compared to $26.2\%$ for YOLO-World-v1-S and $22.7\%$ for YOLO-World-v2-S, using similar backbones on the LVIS minival dataset. Meanwhile, the FPS of DOSOD-S is $57.1\%$ higher than YOLO-World-v1-S and $29.6\%$ higher than YOLO-World-v2-S. Meanwhile, we demonstrate that the DOSOD model facilitates the deployment of edge devices. The codes and models are publicly available at https://github.com/D-Robotics-AI-Lab/DOSOD.

Conditional Outcome Equivalence: A Quantile Alternative to CATE

Conditional quantile treatment effect (CQTE) can provide insight into the effect of a treatment beyond the conditional average treatment effect (CATE). This ability to provide information over multiple quantiles of the response makes CQTE especially valuable in cases where the effect of a treatment is not well-modelled by a location shift, even conditionally on the covariates. Nevertheless, the estimation of CQTE is challenging and often depends upon the smoothness of the individual quantiles as a function of the covariates rather than smoothness of the CQTE itself. This is in stark contrast to CATE where it is possible to obtain high-quality estimates which have less dependency upon the smoothness of the nuisance parameters when the CATE itself is smooth. Moreover, relative smoothness of the CQTE lacks the interpretability of smoothness of the CATE making it less clear whether it is a reasonable assumption to make. We combine the desirable properties of CATE and CQTE by considering a new estimand, the conditional quantile comparator (CQC). The CQC not only retains information about the whole treatment distribution, similar to CQTE, but also having more natural examples of smoothness and is able to leverage simplicity in an auxiliary estimand. We provide finite sample bounds on the error of our estimator, demonstrating its ability to exploit simplicity. We validate our theory in numerical simulations which show that our method produces more accurate estimates than baselines. Finally, we apply our methodology to a study on the effect of employment incentives on earnings across different age groups. We see that our method is able to reveal heterogeneity of the effect across different quantiles.

High-Dimensional Differential Parameter Inference in Exponential Family using Time Score Matching

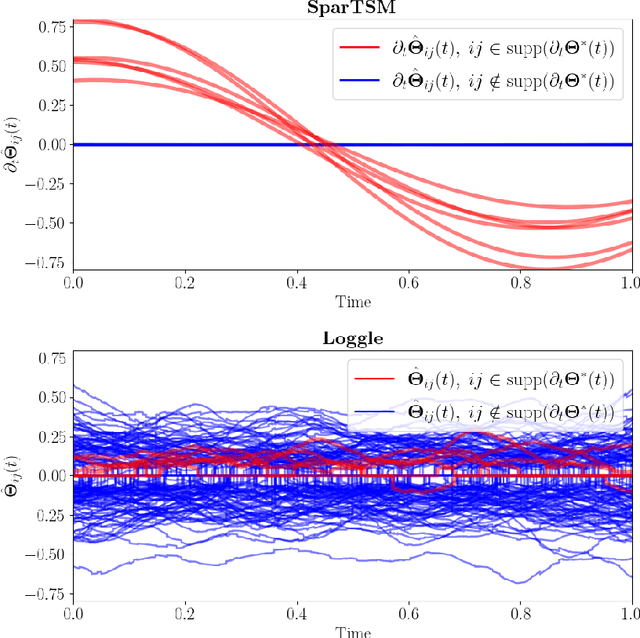
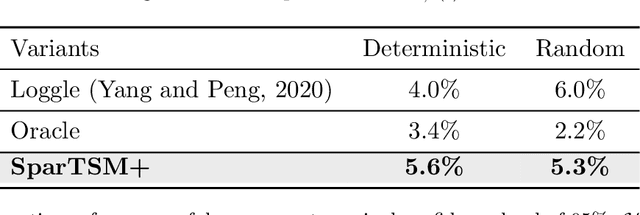
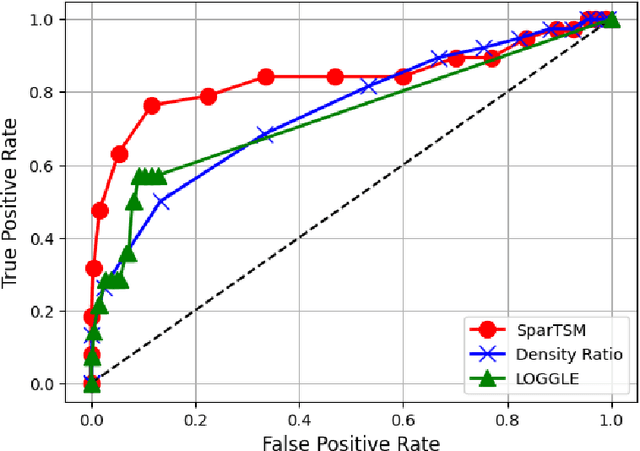
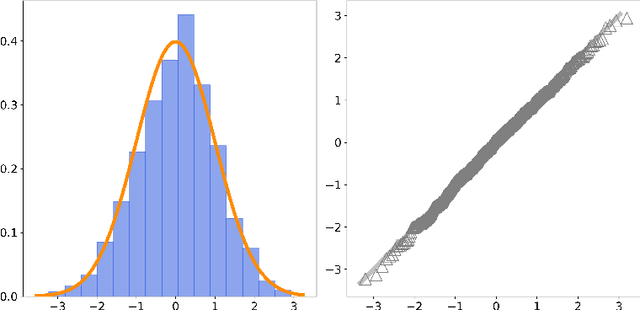
This paper addresses differential inference in time-varying parametric probabilistic models, like graphical models with changing structures. Instead of estimating a high-dimensional model at each time and inferring changes later, we directly learn the differential parameter, i.e., the time derivative of the parameter. The main idea is treating the time score function of an exponential family model as a linear model of the differential parameter for direct estimation. We use time score matching to estimate parameter derivatives. We prove the consistency of a regularized score matching objective and demonstrate the finite-sample normality of a debiased estimator in high-dimensional settings. Our methodology effectively infers differential structures in high-dimensional graphical models, verified on simulated and real-world datasets.

The NING Humanoid: The Concurrent Design and Development of a Dynamic and Agile Platform

The recent surge of interest in agile humanoid robots achieving dynamic tasks like jumping and flipping necessitates the concurrent design of a robot platform that combines exceptional hardware performance with effective control algorithms. This paper introduces the NING Humanoid, an agile and robust platform aimed at achieving human-like athletic capabilities. The NING humanoid features high-torque actuators, a resilient mechanical co-design based on the Centroidal dynamics, and a whole-body model predictive control (WB-MPC) framework. It stands at 1.1 meters tall and weighs 20 kg with 18 degrees of freedom (DOFs). It demonstrates impressive abilities such as walking, push recovery, and stair climbing at a high control bandwidth. Our presentation will encompass a hardware co-design, the control framework, as well as simulation and real-time experiments.