Yakun Wang
Direct Fisher Score Estimation for Likelihood Maximization
Jun 06, 2025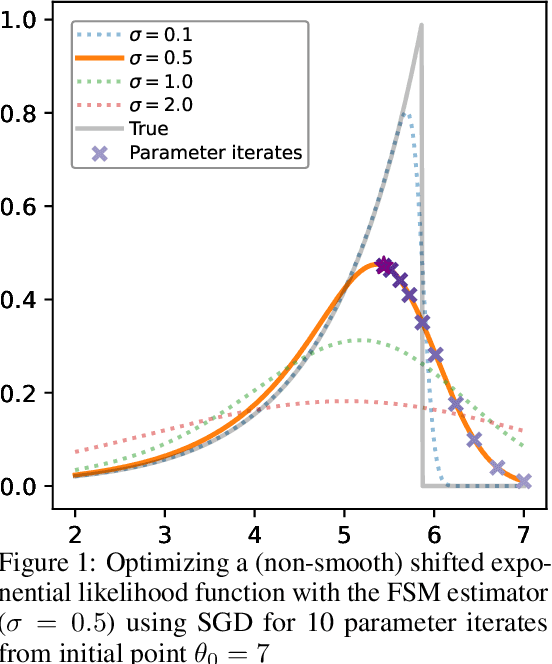
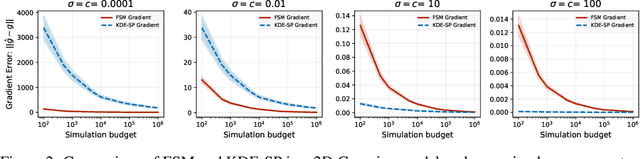
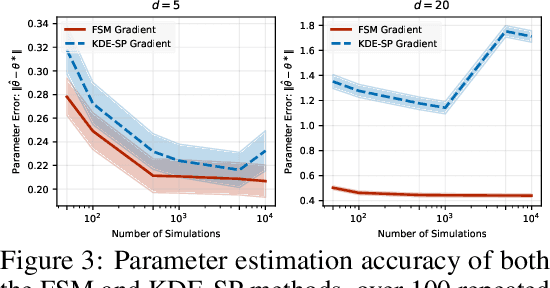
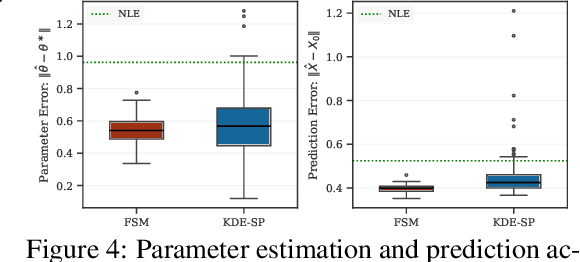
Abstract:We study the problem of likelihood maximization when the likelihood function is intractable but model simulations are readily available. We propose a sequential, gradient-based optimization method that directly models the Fisher score based on a local score matching technique which uses simulations from a localized region around each parameter iterate. By employing a linear parameterization to the surrogate score model, our technique admits a closed-form, least-squares solution. This approach yields a fast, flexible, and efficient approximation to the Fisher score, effectively smoothing the likelihood objective and mitigating the challenges posed by complex likelihood landscapes. We provide theoretical guarantees for our score estimator, including bounds on the bias introduced by the smoothing. Empirical results on a range of synthetic and real-world problems demonstrate the superior performance of our method compared to existing benchmarks.
Guiding Time-Varying Generative Models with Natural Gradients on Exponential Family Manifold
Feb 11, 2025Abstract:Optimising probabilistic models is a well-studied field in statistics. However, its connection with the training of generative models remains largely under-explored. In this paper, we show that the evolution of time-varying generative models can be projected onto an exponential family manifold, naturally creating a link between the parameters of a generative model and those of a probabilistic model. We then train the generative model by moving its projection on the manifold according to the natural gradient descent scheme. This approach also allows us to approximate the natural gradient of the KL divergence efficiently without relying on MCMC for intractable models. Furthermore, we propose particle versions of the algorithm, which feature closed-form update rules for any parametric model within the exponential family. Through toy and real-world experiments, we validate the effectiveness of the proposed algorithms.
Machine Learning Based Probe Skew Correction for High-frequency BH Loop Measurements
Jan 21, 2025



Abstract:Experimental characterization of magnetic components has grown to be increasingly important to understand and model their behaviours in high-frequency PWM converters. The BH loop measurement is the only available approach to separate the core loss as an electrical method, which, however, is suspective to the probe phase skew. As an alternative to the regular de-skew approaches based on hardware, this work proposes a novel machine-learning-based method to identify and correct the probe skew, which builds on the newly discovered correlation between the skew and the shape/trajectory of the measured BH loop. A special technique is proposed to artificially generate the skewed images from measured waveforms as augmented training sets. A machine learning pipeline is developed with the Convolutional Neural Network (CNN) to treat the problem as an image-based prediction task. The trained model has demonstrated a high accuracy in identifying the skew value from a BH loop unseen by the model, which enables the compensation of the skew to yield the corrected core loss value and BH loop.
Smoothness Really Matters: A Simple yet Effective Approach for Unsupervised Graph Domain Adaptation
Dec 16, 2024



Abstract:Unsupervised Graph Domain Adaptation (UGDA) seeks to bridge distribution shifts between domains by transferring knowledge from labeled source graphs to given unlabeled target graphs. Existing UGDA methods primarily focus on aligning features in the latent space learned by graph neural networks (GNNs) across domains, often overlooking structural shifts, resulting in limited effectiveness when addressing structurally complex transfer scenarios. Given the sensitivity of GNNs to local structural features, even slight discrepancies between source and target graphs could lead to significant shifts in node embeddings, thereby reducing the effectiveness of knowledge transfer. To address this issue, we introduce a novel approach for UGDA called Target-Domain Structural Smoothing (TDSS). TDSS is a simple and effective method designed to perform structural smoothing directly on the target graph, thereby mitigating structural distribution shifts and ensuring the consistency of node representations. Specifically, by integrating smoothing techniques with neighborhood sampling, TDSS maintains the structural coherence of the target graph while mitigating the risk of over-smoothing. Our theoretical analysis shows that TDSS effectively reduces target risk by improving model smoothness. Empirical results on three real-world datasets demonstrate that TDSS outperforms recent state-of-the-art baselines, achieving significant improvements across six transfer scenarios. The code is available in https://github.com/cwei01/TDSS.
Optimizing Long-tailed Link Prediction in Graph Neural Networks through Structure Representation Enhancement
Jul 30, 2024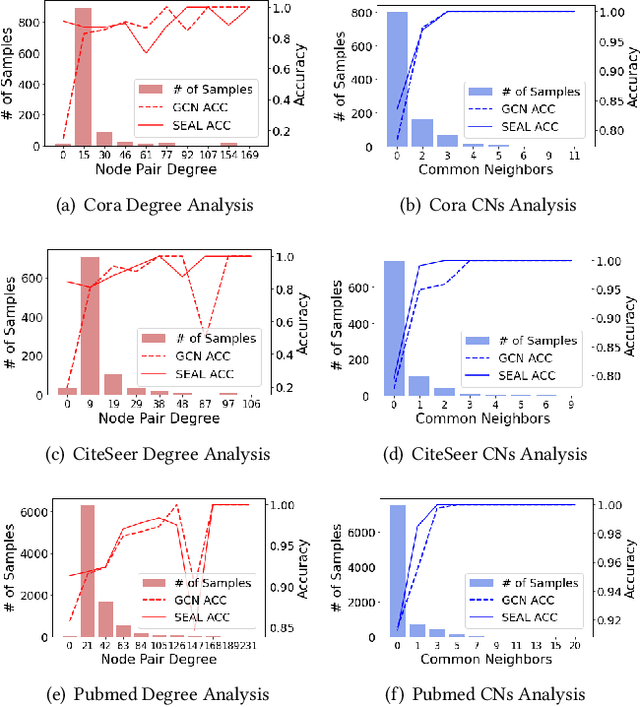
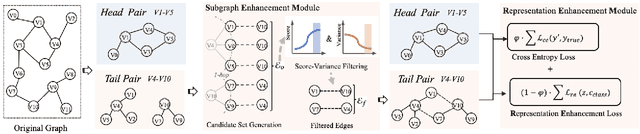
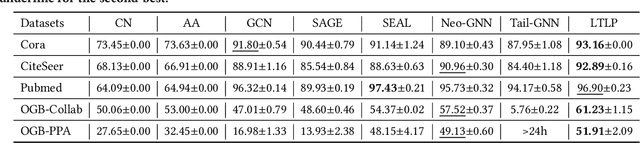
Abstract:Link prediction, as a fundamental task for graph neural networks (GNNs), has boasted significant progress in varied domains. Its success is typically influenced by the expressive power of node representation, but recent developments reveal the inferior performance of low-degree nodes owing to their sparse neighbor connections, known as the degree-based long-tailed problem. Will the degree-based long-tailed distribution similarly constrain the efficacy of GNNs on link prediction? Unexpectedly, our study reveals that only a mild correlation exists between node degree and predictive accuracy, and more importantly, the number of common neighbors between node pairs exhibits a strong correlation with accuracy. Considering node pairs with less common neighbors, i.e., tail node pairs, make up a substantial fraction of the dataset but achieve worse performance, we propose that link prediction also faces the long-tailed problem. Therefore, link prediction of GNNs is greatly hindered by the tail node pairs. After knowing the weakness of link prediction, a natural question is how can we eliminate the negative effects of the skewed long-tailed distribution on common neighbors so as to improve the performance of link prediction? Towards this end, we introduce our long-tailed framework (LTLP), which is designed to enhance the performance of tail node pairs on link prediction by increasing common neighbors. Two key modules in LTLP respectively supplement high-quality edges for tail node pairs and enforce representational alignment between head and tail node pairs within the same category, thereby improving the performance of tail node pairs.
Not All Negatives Are Worth Attending to: Meta-Bootstrapping Negative Sampling Framework for Link Prediction
Dec 12, 2023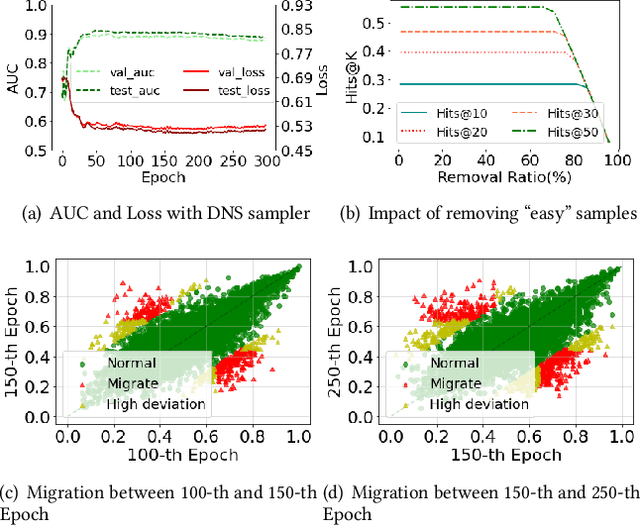
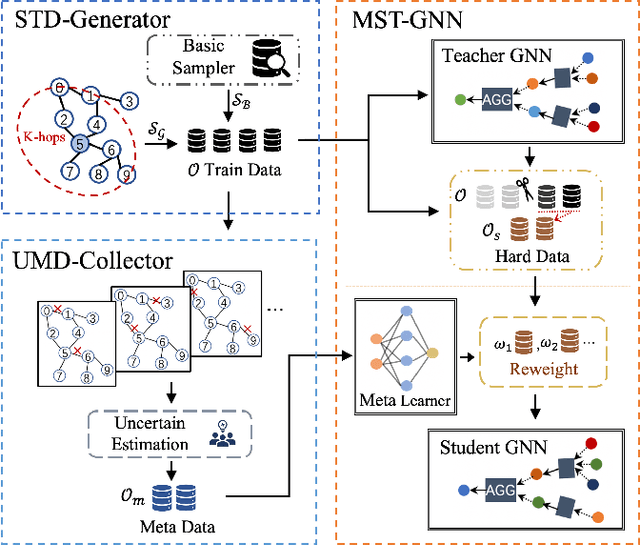
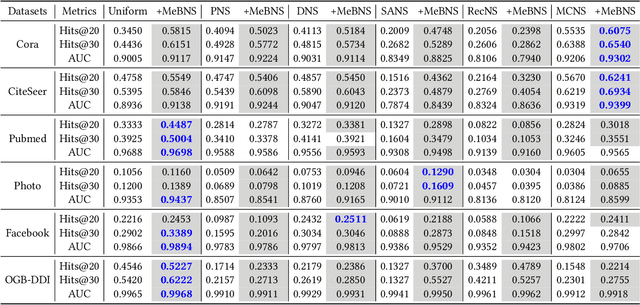
Abstract:The rapid development of graph neural networks (GNNs) encourages the rising of link prediction, achieving promising performance with various applications. Unfortunately, through a comprehensive analysis, we surprisingly find that current link predictors with dynamic negative samplers (DNSs) suffer from the migration phenomenon between "easy" and "hard" samples, which goes against the preference of DNS of choosing "hard" negatives, thus severely hindering capability. Towards this end, we propose the MeBNS framework, serving as a general plugin that can potentially improve current negative sampling based link predictors. In particular, we elaborately devise a Meta-learning Supported Teacher-student GNN (MST-GNN) that is not only built upon teacher-student architecture for alleviating the migration between "easy" and "hard" samples but also equipped with a meta learning based sample re-weighting module for helping the student GNN distinguish "hard" samples in a fine-grained manner. To effectively guide the learning of MST-GNN, we prepare a Structure enhanced Training Data Generator (STD-Generator) and an Uncertainty based Meta Data Collector (UMD-Collector) for supporting the teacher and student GNN, respectively. Extensive experiments show that the MeBNS achieves remarkable performance across six link prediction benchmark datasets.
An Effective Graph Learning based Approach for Temporal Link Prediction: The First Place of WSDM Cup 2022
Mar 01, 2022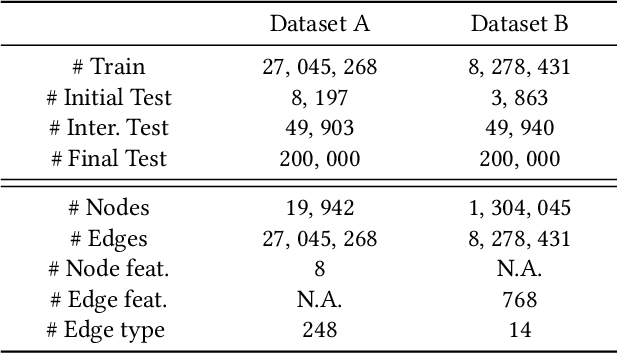


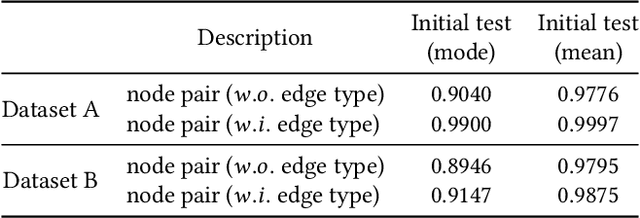
Abstract:Temporal link prediction, as one of the most crucial work in temporal graphs, has attracted lots of attention from the research area. The WSDM Cup 2022 seeks for solutions that predict the existence probabilities of edges within time spans over temporal graph. This paper introduces the solution of AntGraph, which wins the 1st place in the competition. We first analysis the theoretical upper-bound of the performance by removing temporal information, which implies that only structure and attribute information on the graph could achieve great performance. Based on this hypothesis, then we introduce several well-designed features. Finally, experiments conducted on the competition datasets show the superiority of our proposal, which achieved AUC score of 0.666 on dataset A and 0.902 on dataset B, the ablation studies also prove the efficiency of each feature. Code is publicly available at https://github.com/im0qianqian/WSDM2022TGP-AntGraph.
Adaptive Bayesian Sum of Trees Model for Covariate Dependent Spectral Analysis
Sep 29, 2021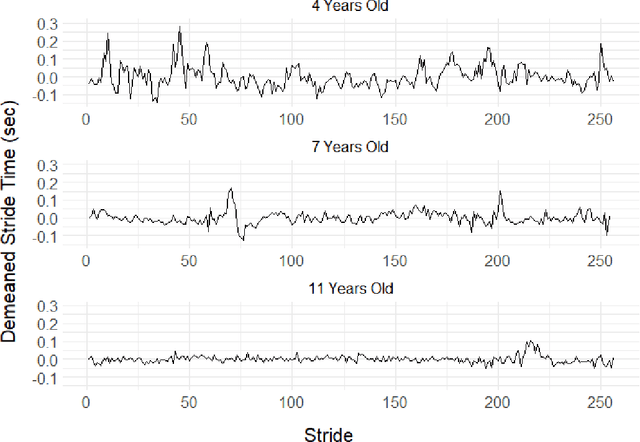

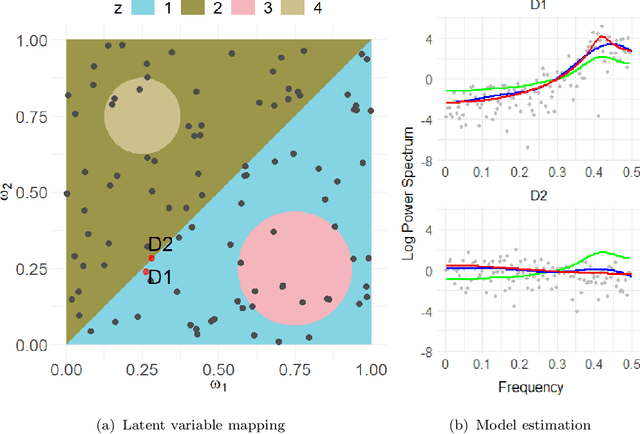
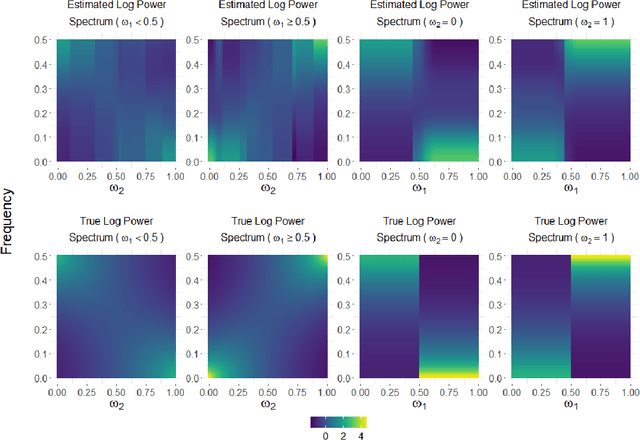
Abstract:This article introduces a flexible and adaptive nonparametric method for estimating the association between multiple covariates and power spectra of multiple time series. The proposed approach uses a Bayesian sum of trees model to capture complex dependencies and interactions between covariates and the power spectrum, which are often observed in studies of biomedical time series. Local power spectra corresponding to terminal nodes within trees are estimated nonparametrically using Bayesian penalized linear splines. The trees are considered to be random and fit using a Bayesian backfitting Markov chain Monte Carlo (MCMC) algorithm that sequentially considers tree modifications via reversible-jump MCMC techniques. For high-dimensional covariates, a sparsity-inducing Dirichlet hyperprior on tree splitting proportions is considered, which provides sparse estimation of covariate effects and efficient variable selection. By averaging over the posterior distribution of trees, the proposed method can recover both smooth and abrupt changes in the power spectrum across multiple covariates. Empirical performance is evaluated via simulations to demonstrate the proposed method's ability to accurately recover complex relationships and interactions. The proposed methodology is used to study gait maturation in young children by evaluating age-related changes in power spectra of stride interval time series in the presence of other covariates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge