Adaptive Bayesian Sum of Trees Model for Covariate Dependent Spectral Analysis

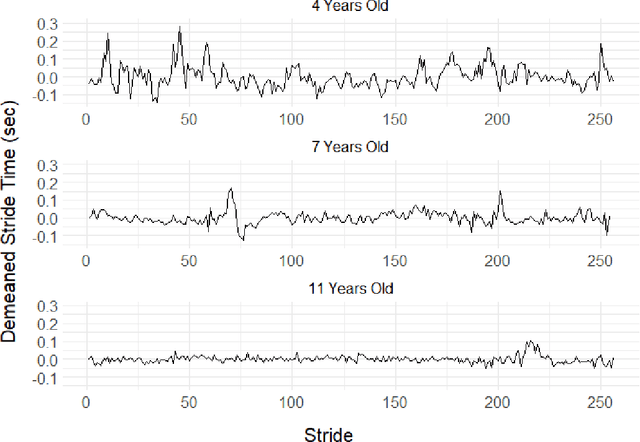
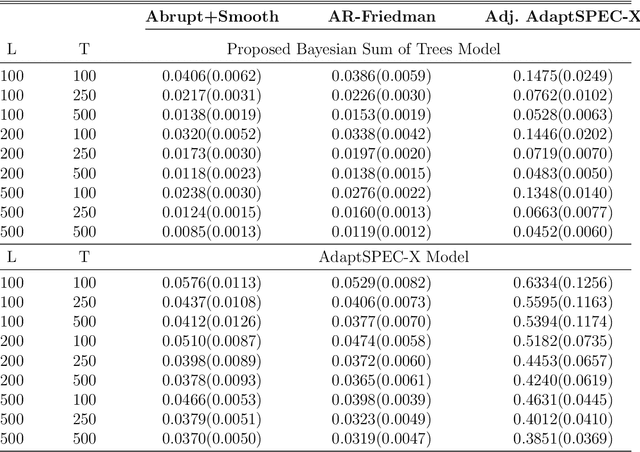
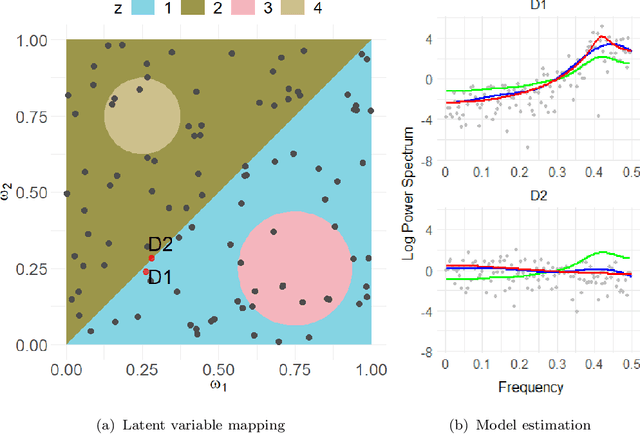
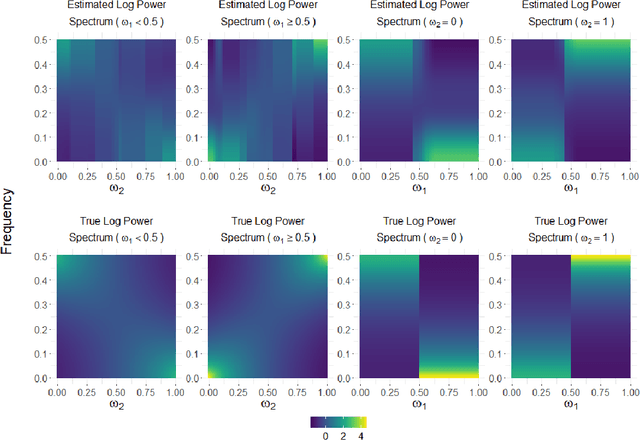
This article introduces a flexible and adaptive nonparametric method for estimating the association between multiple covariates and power spectra of multiple time series. The proposed approach uses a Bayesian sum of trees model to capture complex dependencies and interactions between covariates and the power spectrum, which are often observed in studies of biomedical time series. Local power spectra corresponding to terminal nodes within trees are estimated nonparametrically using Bayesian penalized linear splines. The trees are considered to be random and fit using a Bayesian backfitting Markov chain Monte Carlo (MCMC) algorithm that sequentially considers tree modifications via reversible-jump MCMC techniques. For high-dimensional covariates, a sparsity-inducing Dirichlet hyperprior on tree splitting proportions is considered, which provides sparse estimation of covariate effects and efficient variable selection. By averaging over the posterior distribution of trees, the proposed method can recover both smooth and abrupt changes in the power spectrum across multiple covariates. Empirical performance is evaluated via simulations to demonstrate the proposed method's ability to accurately recover complex relationships and interactions. The proposed methodology is used to study gait maturation in young children by evaluating age-related changes in power spectra of stride interval time series in the presence of other covariates.