Hongrui Liu
IceBerg: Debiased Self-Training for Class-Imbalanced Node Classification
Feb 10, 2025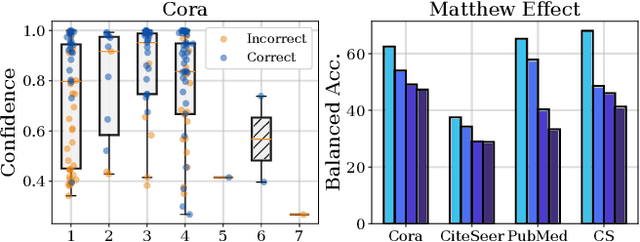
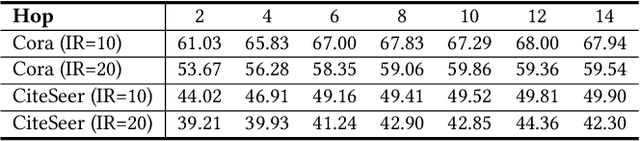
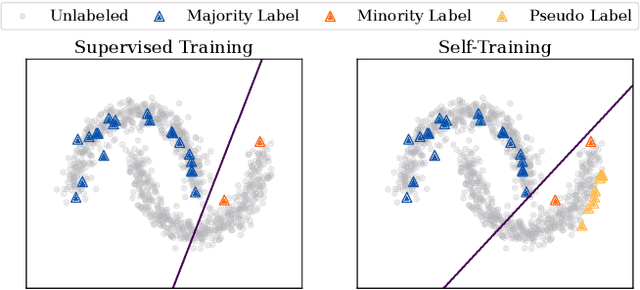
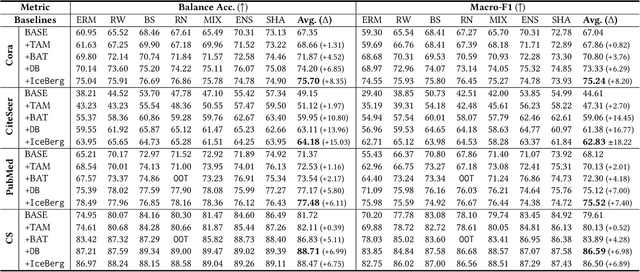
Abstract:Graph Neural Networks (GNNs) have achieved great success in dealing with non-Euclidean graph-structured data and have been widely deployed in many real-world applications. However, their effectiveness is often jeopardized under class-imbalanced training sets. Most existing studies have analyzed class-imbalanced node classification from a supervised learning perspective, but they do not fully utilize the large number of unlabeled nodes in semi-supervised scenarios. We claim that the supervised signal is just the tip of the iceberg and a large number of unlabeled nodes have not yet been effectively utilized. In this work, we propose IceBerg, a debiased self-training framework to address the class-imbalanced and few-shot challenges for GNNs at the same time. Specifically, to figure out the Matthew effect and label distribution shift in self-training, we propose Double Balancing, which can largely improve the performance of existing baselines with just a few lines of code as a simple plug-and-play module. Secondly, to enhance the long-range propagation capability of GNNs, we disentangle the propagation and transformation operations of GNNs. Therefore, the weak supervision signals can propagate more effectively to address the few-shot issue. In summary, we find that leveraging unlabeled nodes can significantly enhance the performance of GNNs in class-imbalanced and few-shot scenarios, and even small, surgical modifications can lead to substantial performance improvements. Systematic experiments on benchmark datasets show that our method can deliver considerable performance gain over existing class-imbalanced node classification baselines. Additionally, due to IceBerg's outstanding ability to leverage unsupervised signals, it also achieves state-of-the-art results in few-shot node classification scenarios. The code of IceBerg is available at: https://github.com/ZhixunLEE/IceBerg.
Optimizing Long-tailed Link Prediction in Graph Neural Networks through Structure Representation Enhancement
Jul 30, 2024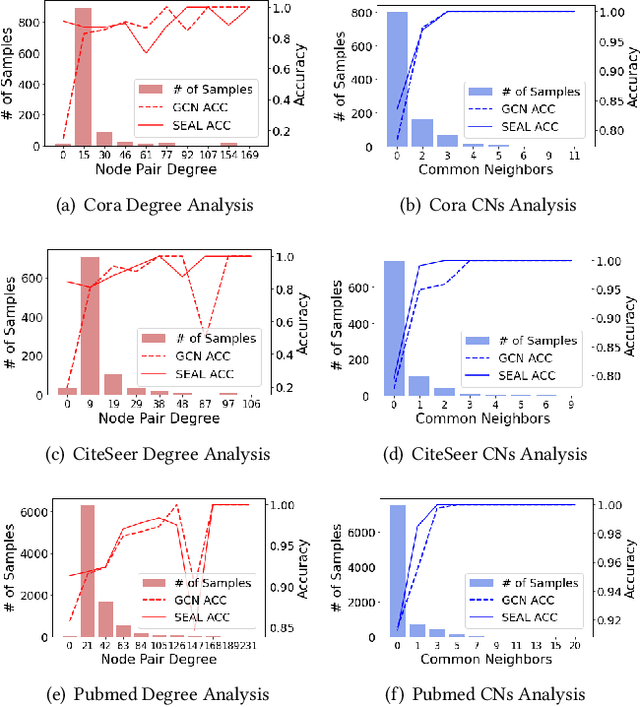
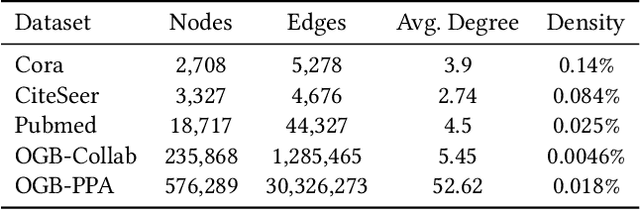
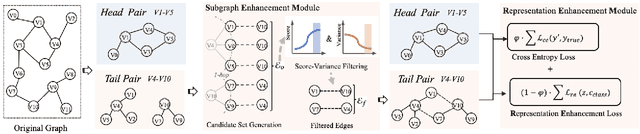
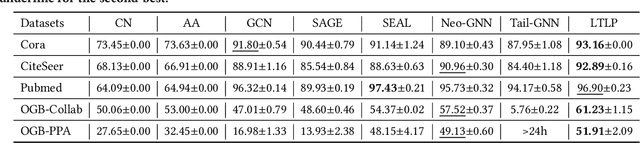
Abstract:Link prediction, as a fundamental task for graph neural networks (GNNs), has boasted significant progress in varied domains. Its success is typically influenced by the expressive power of node representation, but recent developments reveal the inferior performance of low-degree nodes owing to their sparse neighbor connections, known as the degree-based long-tailed problem. Will the degree-based long-tailed distribution similarly constrain the efficacy of GNNs on link prediction? Unexpectedly, our study reveals that only a mild correlation exists between node degree and predictive accuracy, and more importantly, the number of common neighbors between node pairs exhibits a strong correlation with accuracy. Considering node pairs with less common neighbors, i.e., tail node pairs, make up a substantial fraction of the dataset but achieve worse performance, we propose that link prediction also faces the long-tailed problem. Therefore, link prediction of GNNs is greatly hindered by the tail node pairs. After knowing the weakness of link prediction, a natural question is how can we eliminate the negative effects of the skewed long-tailed distribution on common neighbors so as to improve the performance of link prediction? Towards this end, we introduce our long-tailed framework (LTLP), which is designed to enhance the performance of tail node pairs on link prediction by increasing common neighbors. Two key modules in LTLP respectively supplement high-quality edges for tail node pairs and enforce representational alignment between head and tail node pairs within the same category, thereby improving the performance of tail node pairs.
A Generalized Neural Diffusion Framework on Graphs
Dec 14, 2023



Abstract:Recent studies reveal the connection between GNNs and the diffusion process, which motivates many diffusion-based GNNs to be proposed. However, since these two mechanisms are closely related, one fundamental question naturally arises: Is there a general diffusion framework that can formally unify these GNNs? The answer to this question can not only deepen our understanding of the learning process of GNNs, but also may open a new door to design a broad new class of GNNs. In this paper, we propose a general diffusion equation framework with the fidelity term, which formally establishes the relationship between the diffusion process with more GNNs. Meanwhile, with this framework, we identify one characteristic of graph diffusion networks, i.e., the current neural diffusion process only corresponds to the first-order diffusion equation. However, by an experimental investigation, we show that the labels of high-order neighbors actually exhibit monophily property, which induces the similarity based on labels among high-order neighbors without requiring the similarity among first-order neighbors. This discovery motives to design a new high-order neighbor-aware diffusion equation, and derive a new type of graph diffusion network (HiD-Net) based on the framework. With the high-order diffusion equation, HiD-Net is more robust against attacks and works on both homophily and heterophily graphs. We not only theoretically analyze the relation between HiD-Net with high-order random walk, but also provide a theoretical convergence guarantee. Extensive experimental results well demonstrate the effectiveness of HiD-Net over state-of-the-art graph diffusion networks.
Single-pixel imaging based on deep learning
Oct 25, 2023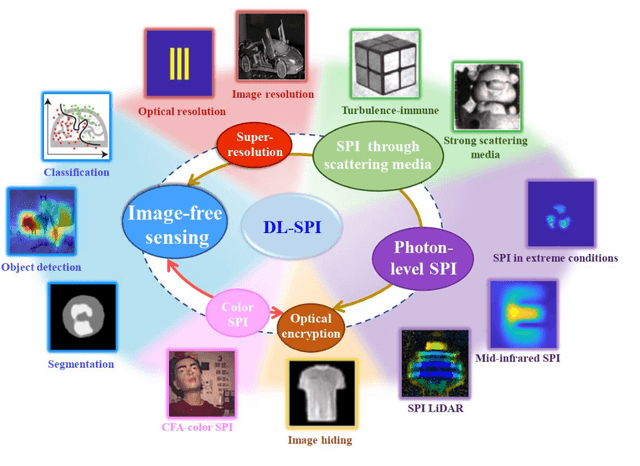
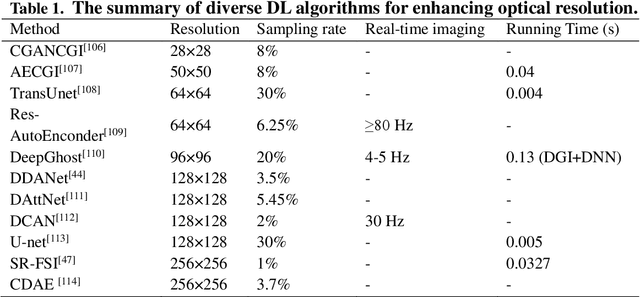
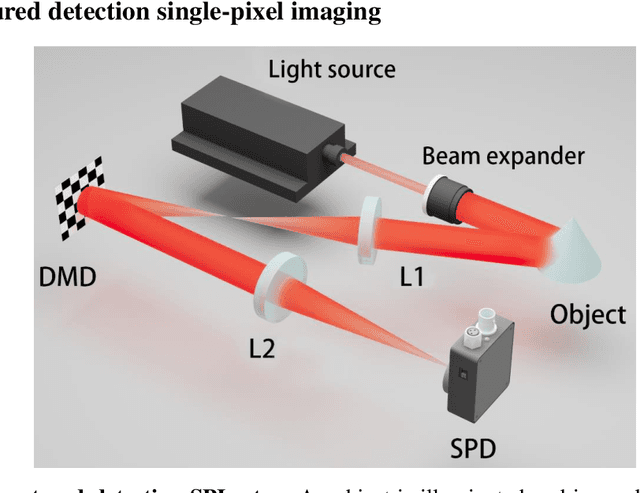
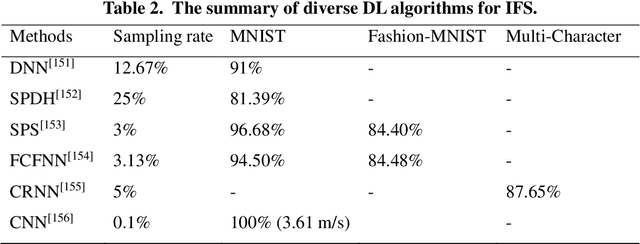
Abstract:Since the advent of single-pixel imaging and machine learning, both fields have flourished, but followed parallel tracks. Until recently, machine learning, especially deep learning, has demonstrated effectiveness in delivering high-quality solutions across various application domains of single-pixel imaging. This article comprehensively reviews the research of single-pixel imaging technology based on deep learning. From the basic principles of single-pixel imaging and deep learning, the principles and implementation methods of single-pixel imaging based on deep learning are described in detail. Then, the research status and development trend of single-pixel imaging based on deep learning in various domains are analyzed, including super-resolution single-pixel imaging, single-pixel imaging through scattering media, photon-level single-pixel imaging, optical encryption based on single-pixel imaging, color single-pixel imaging, and image-free sensing. Finally, this review explores the limitations in the ongoing research, while offers the delivering insights into prospective avenues for future research.
Quaternion-valued Correlation Learning for Few-Shot Semantic Segmentation
May 15, 2023



Abstract:Few-shot segmentation (FSS) aims to segment unseen classes given only a few annotated samples. Encouraging progress has been made for FSS by leveraging semantic features learned from base classes with sufficient training samples to represent novel classes. The correlation-based methods lack the ability to consider interaction of the two subspace matching scores due to the inherent nature of the real-valued 2D convolutions. In this paper, we introduce a quaternion perspective on correlation learning and propose a novel Quaternion-valued Correlation Learning Network (QCLNet), with the aim to alleviate the computational burden of high-dimensional correlation tensor and explore internal latent interaction between query and support images by leveraging operations defined by the established quaternion algebra. Specifically, our QCLNet is formulated as a hyper-complex valued network and represents correlation tensors in the quaternion domain, which uses quaternion-valued convolution to explore the external relations of query subspace when considering the hidden relationship of the support sub-dimension in the quaternion space. Extensive experiments on the PASCAL-5i and COCO-20i datasets demonstrate that our method outperforms the existing state-of-the-art methods effectively. Our code is available at https://github.com/zwzheng98/QCLNet
Confidence May Cheat: Self-Training on Graph Neural Networks under Distribution Shift
Jan 27, 2022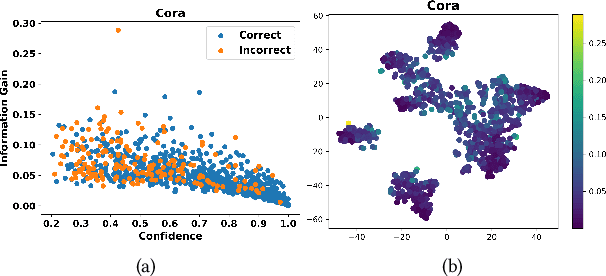
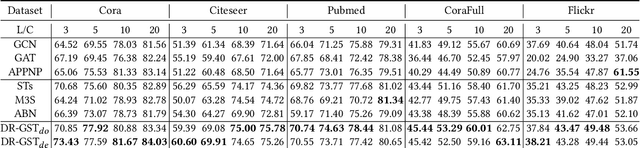
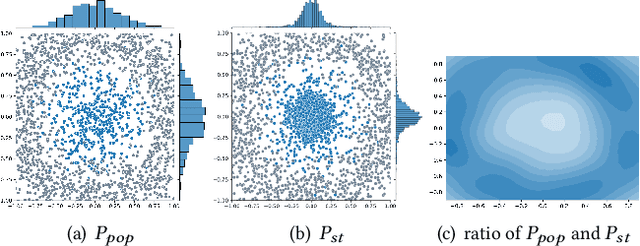
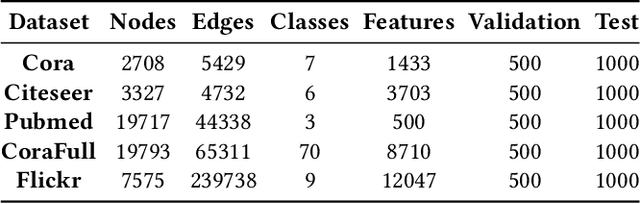
Abstract:Graph Convolutional Networks (GCNs) have recently attracted vast interest and achieved state-of-the-art performance on graphs, but its success could typically hinge on careful training with amounts of expensive and time-consuming labeled data. To alleviate labeled data scarcity, self-training methods have been widely adopted on graphs by labeling high-confidence unlabeled nodes and then adding them to the training step. In this line, we empirically make a thorough study for current self-training methods on graphs. Surprisingly, we find that high-confidence unlabeled nodes are not always useful, and even introduce the distribution shift issue between the original labeled dataset and the augmented dataset by self-training, severely hindering the capability of self-training on graphs. To this end, in this paper, we propose a novel Distribution Recovered Graph Self-Training framework (DR-GST), which could recover the distribution of the original labeled dataset. Specifically, we first prove the equality of loss function in self-training framework under the distribution shift case and the population distribution if each pseudo-labeled node is weighted by a proper coefficient. Considering the intractability of the coefficient, we then propose to replace the coefficient with the information gain after observing the same changing trend between them, where information gain is respectively estimated via both dropout variational inference and dropedge variational inference in DR-GST. However, such a weighted loss function will enlarge the impact of incorrect pseudo labels. As a result, we apply the loss correction method to improve the quality of pseudo labels. Both our theoretical analysis and extensive experiments on five benchmark datasets demonstrate the effectiveness of the proposed DR-GST, as well as each well-designed component in DR-GST.
Be Confident! Towards Trustworthy Graph Neural Networks via Confidence Calibration
Sep 29, 2021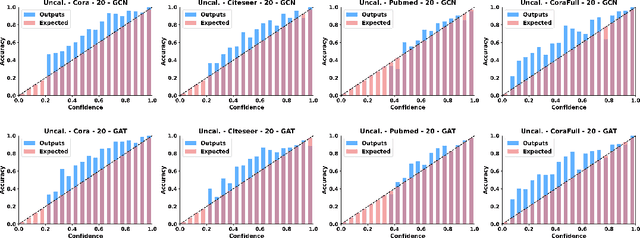
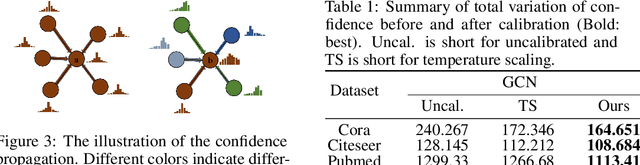
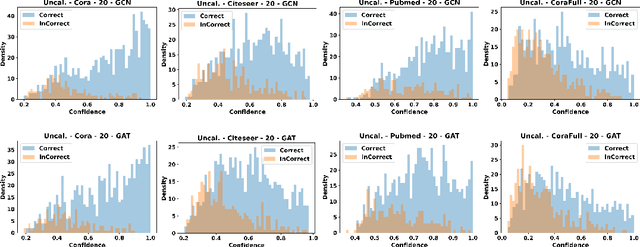
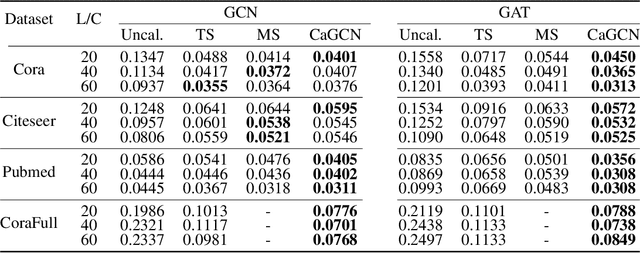
Abstract:Despite Graph Neural Networks (GNNs) have achieved remarkable accuracy, whether the results are trustworthy is still unexplored. Previous studies suggest that many modern neural networks are over-confident on the predictions, however, surprisingly, we discover that GNNs are primarily in the opposite direction, i.e., GNNs are under-confident. Therefore, the confidence calibration for GNNs is highly desired. In this paper, we propose a novel trustworthy GNN model by designing a topology-aware post-hoc calibration function. Specifically, we first verify that the confidence distribution in a graph has homophily property, and this finding inspires us to design a calibration GNN model (CaGCN) to learn the calibration function. CaGCN is able to obtain a unique transformation from logits of GNNs to the calibrated confidence for each node, meanwhile, such transformation is able to preserve the order between classes, satisfying the accuracy-preserving property. Moreover, we apply the calibration GNN to self-training framework, showing that more trustworthy pseudo labels can be obtained with the calibrated confidence and further improve the performance. Extensive experiments demonstrate the effectiveness of our proposed model in terms of both calibration and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge