Confidence May Cheat: Self-Training on Graph Neural Networks under Distribution Shift
Paper and Code
Jan 27, 2022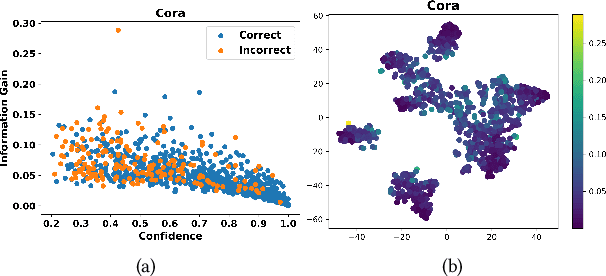
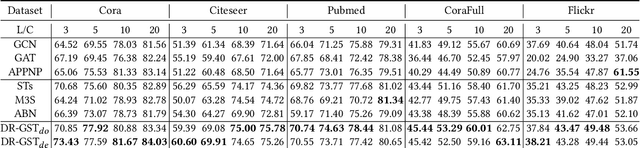
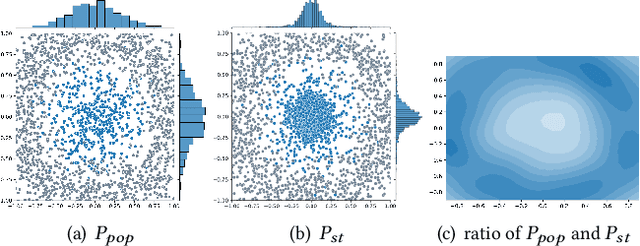
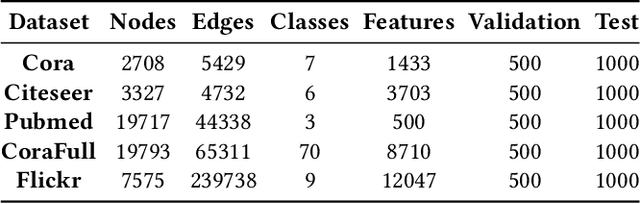
Graph Convolutional Networks (GCNs) have recently attracted vast interest and achieved state-of-the-art performance on graphs, but its success could typically hinge on careful training with amounts of expensive and time-consuming labeled data. To alleviate labeled data scarcity, self-training methods have been widely adopted on graphs by labeling high-confidence unlabeled nodes and then adding them to the training step. In this line, we empirically make a thorough study for current self-training methods on graphs. Surprisingly, we find that high-confidence unlabeled nodes are not always useful, and even introduce the distribution shift issue between the original labeled dataset and the augmented dataset by self-training, severely hindering the capability of self-training on graphs. To this end, in this paper, we propose a novel Distribution Recovered Graph Self-Training framework (DR-GST), which could recover the distribution of the original labeled dataset. Specifically, we first prove the equality of loss function in self-training framework under the distribution shift case and the population distribution if each pseudo-labeled node is weighted by a proper coefficient. Considering the intractability of the coefficient, we then propose to replace the coefficient with the information gain after observing the same changing trend between them, where information gain is respectively estimated via both dropout variational inference and dropedge variational inference in DR-GST. However, such a weighted loss function will enlarge the impact of incorrect pseudo labels. As a result, we apply the loss correction method to improve the quality of pseudo labels. Both our theoretical analysis and extensive experiments on five benchmark datasets demonstrate the effectiveness of the proposed DR-GST, as well as each well-designed component in DR-GST.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge