Quaternion-valued Correlation Learning for Few-Shot Semantic Segmentation

Few-shot segmentation (FSS) aims to segment unseen classes given only a few annotated samples. Encouraging progress has been made for FSS by leveraging semantic features learned from base classes with sufficient training samples to represent novel classes. The correlation-based methods lack the ability to consider interaction of the two subspace matching scores due to the inherent nature of the real-valued 2D convolutions. In this paper, we introduce a quaternion perspective on correlation learning and propose a novel Quaternion-valued Correlation Learning Network (QCLNet), with the aim to alleviate the computational burden of high-dimensional correlation tensor and explore internal latent interaction between query and support images by leveraging operations defined by the established quaternion algebra. Specifically, our QCLNet is formulated as a hyper-complex valued network and represents correlation tensors in the quaternion domain, which uses quaternion-valued convolution to explore the external relations of query subspace when considering the hidden relationship of the support sub-dimension in the quaternion space. Extensive experiments on the PASCAL-5i and COCO-20i datasets demonstrate that our method outperforms the existing state-of-the-art methods effectively. Our code is available at https://github.com/zwzheng98/QCLNet

Sparse Representation Based Augmented Multinomial Logistic Extreme Learning Machine with Weighted Composite Features for Spectral Spatial Hyperspectral Image Classification

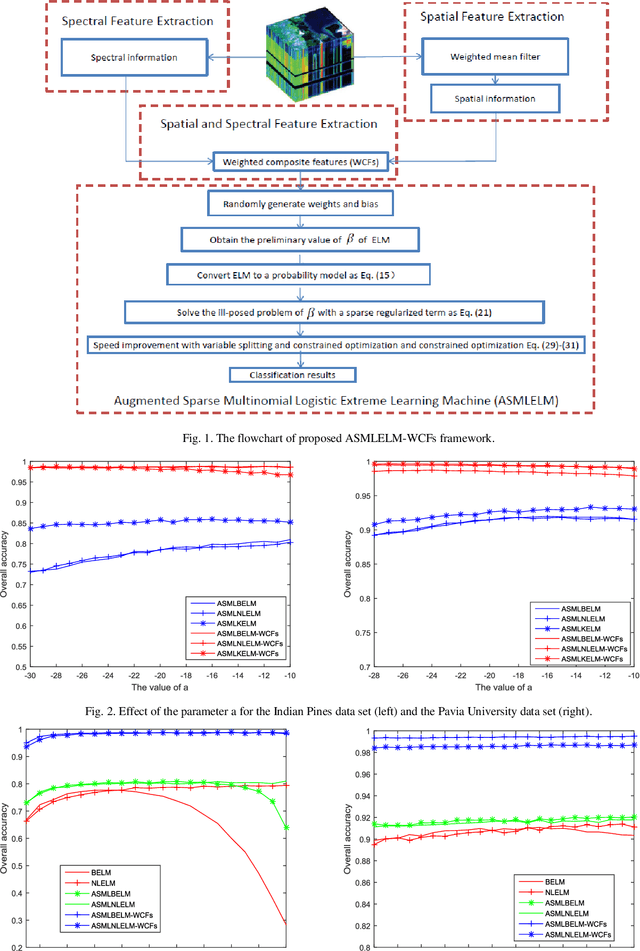
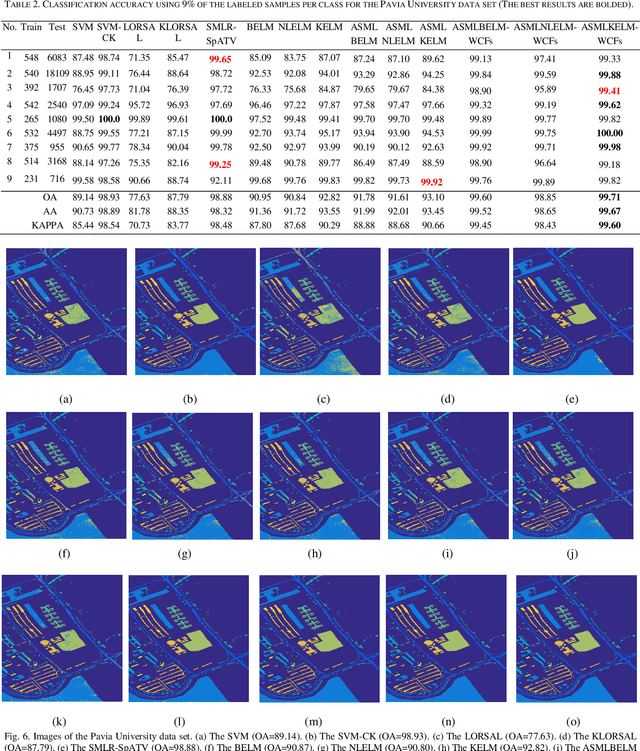
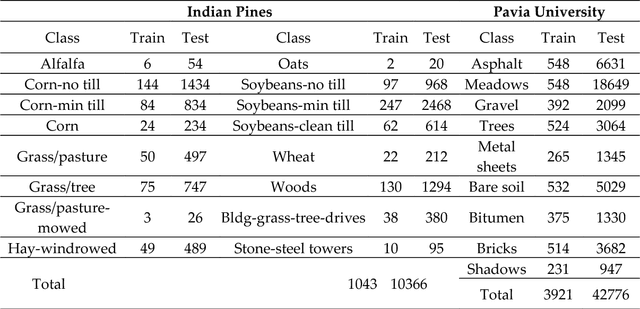
Although extreme learning machine (ELM) has been successfully applied to a number of pattern recognition problems, it fails to pro-vide sufficient good results in hyperspectral image (HSI) classification due to two main drawbacks. The first is due to the random weights and bias of ELM, which may lead to ill-posed problems. The second is the lack of spatial information for classification. To tackle these two problems, in this paper, we propose a new framework for ELM based spectral-spatial classification of HSI, where probabilistic modelling with sparse representation and weighted composite features (WCF) are employed respectively to derive the op-timized output weights and extract spatial features. First, the ELM is represented as a concave logarithmic likelihood function under statistical modelling using the maximum a posteriori (MAP). Second, the sparse representation is applied to the Laplacian prior to effi-ciently determine a logarithmic posterior with a unique maximum in order to solve the ill-posed problem of ELM. The variable splitting and the augmented Lagrangian are subsequently used to further reduce the computation complexity of the proposed algorithm and it has been proven a more efficient method for speed improvement. Third, the spatial information is extracted using the weighted compo-site features (WCFs) to construct the spectral-spatial classification framework. In addition, the lower bound of the proposed method is derived by a rigorous mathematical proof. Experimental results on two publicly available HSI data sets demonstrate that the proposed methodology outperforms ELM and a number of state-of-the-art approaches.

Linear vs Nonlinear Extreme Learning Machine for Spectral-Spatial Classification of Hyperspectral Image

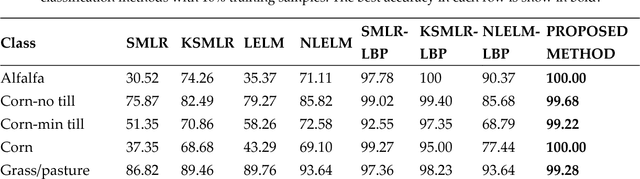
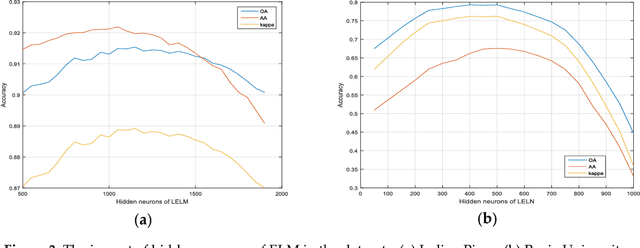
As a new machine learning approach, extreme learning machine (ELM) has received wide attentions due to its good performances. However, when directly applied to the hyperspectral image (HSI) classification, the recognition rate is too low. This is because ELM does not use the spatial information which is very important for HSI classification. In view of this, this paper proposes a new framework for spectral-spatial classification of HSI by combining ELM with loopy belief propagation (LBP). The original ELM is linear, and the nonlinear ELMs (or Kernel ELMs) are the improvement of linear ELM (LELM). However, based on lots of experiments and analysis, we found out that the LELM is a better choice than nonlinear ELM for spectral-spatial classification of HSI. Furthermore, we exploit the marginal probability distribution that uses the whole information in the HSI and learn such distribution using the LBP. The proposed method not only maintain the fast speed of ELM, but also greatly improves the accuracy of classification. The experimental results in the well-known HSI data sets, Indian Pines and Pavia University, demonstrate the good performances of the proposed method.

Does Normalization Methods Play a Role for Hyperspectral Image Classification?

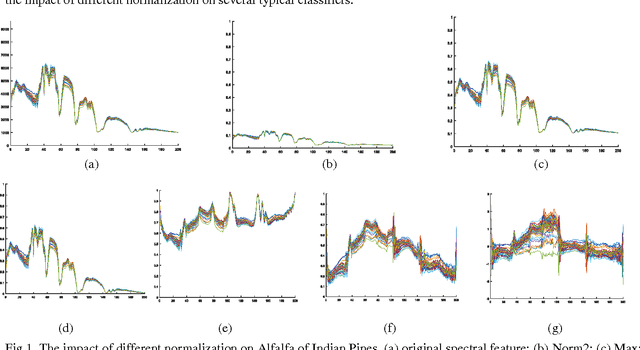
For Hyperspectral image (HSI) datasets, each class have their salient feature and classifiers classify HSI datasets according to the class's saliency features, however, there will be different salient features when use different normalization method. In this letter, we report the effect on classifiers by different normalization methods and recommend the best normalization methods for classifier after analyzing the impact of different normalization methods on classifiers. Pavia University datasets, Indian Pines datasets and Kennedy Space Center datasets will apply to several typical classifiers in order to evaluate and analysis the impact of different normalization methods on typical classifiers.

Extreme Sparse Multinomial Logistic Regression: A Fast and Robust Framework for Hyperspectral Image Classification

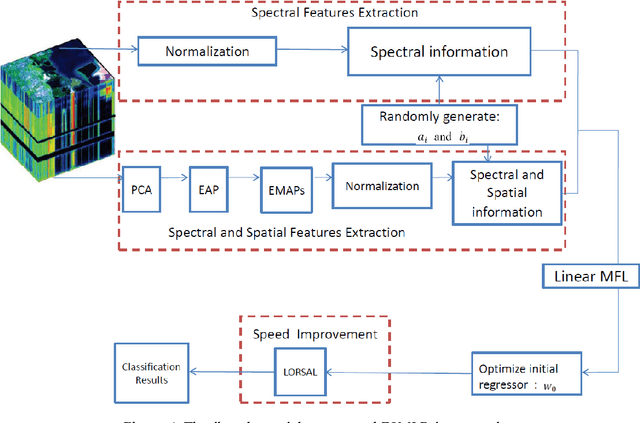
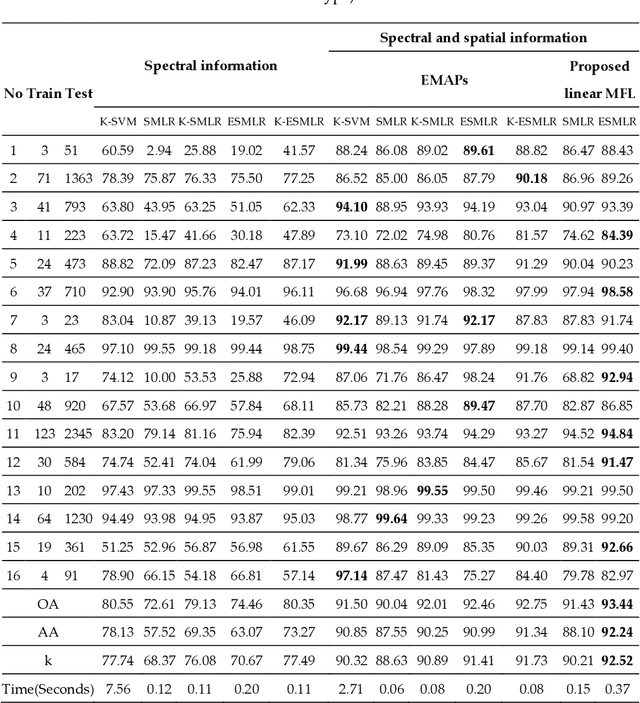
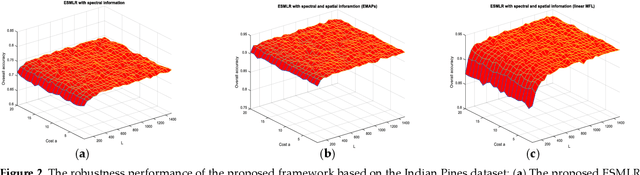
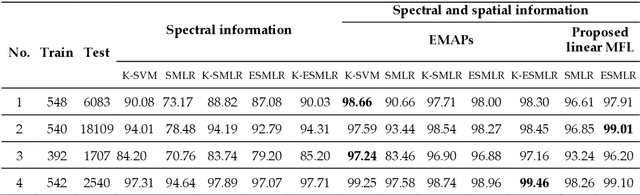
Although the sparse multinomial logistic regression (SMLR) has provided a useful tool for sparse classification, it suffers from inefficacy in dealing with high dimensional features and manually set initial regressor values. This has significantly constrained its applications for hyperspectral image (HSI) classification. In order to tackle these two drawbacks, an extreme sparse multinomial logistic regression (ESMLR) is proposed for effective classification of HSI. First, the HSI dataset is projected to a new feature space with randomly generated weight and bias. Second, an optimization model is established by the Lagrange multiplier method and the dual principle to automatically determine a good initial regressor for SMLR via minimizing the training error and the regressor value. Furthermore, the extended multi-attribute profiles (EMAPs) are utilized for extracting both the spectral and spatial features. A combinational linear multiple features learning (MFL) method is proposed to further enhance the features extracted by ESMLR and EMAPs. Finally, the logistic regression via the variable splitting and the augmented Lagrangian (LORSAL) is adopted in the proposed framework for reducing the computational time. Experiments are conducted on two well-known HSI datasets, namely the Indian Pines dataset and the Pavia University dataset, which have shown the fast and robust performance of the proposed ESMLR framework.