Be Confident! Towards Trustworthy Graph Neural Networks via Confidence Calibration
Paper and Code
Sep 29, 2021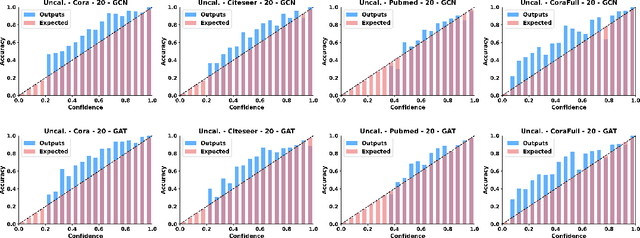
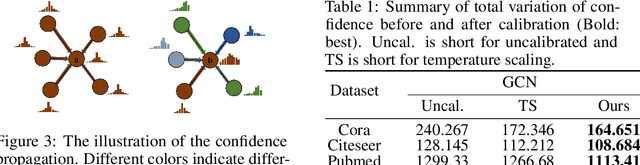
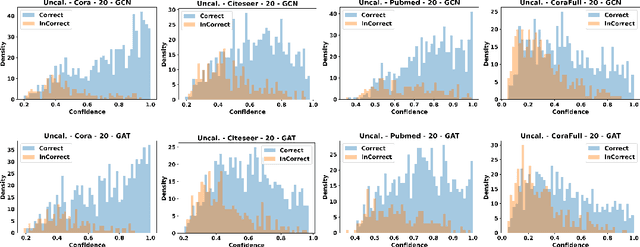
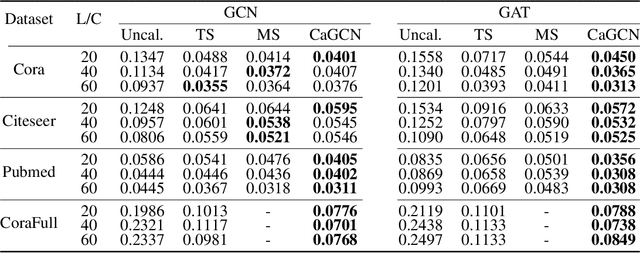
Despite Graph Neural Networks (GNNs) have achieved remarkable accuracy, whether the results are trustworthy is still unexplored. Previous studies suggest that many modern neural networks are over-confident on the predictions, however, surprisingly, we discover that GNNs are primarily in the opposite direction, i.e., GNNs are under-confident. Therefore, the confidence calibration for GNNs is highly desired. In this paper, we propose a novel trustworthy GNN model by designing a topology-aware post-hoc calibration function. Specifically, we first verify that the confidence distribution in a graph has homophily property, and this finding inspires us to design a calibration GNN model (CaGCN) to learn the calibration function. CaGCN is able to obtain a unique transformation from logits of GNNs to the calibrated confidence for each node, meanwhile, such transformation is able to preserve the order between classes, satisfying the accuracy-preserving property. Moreover, we apply the calibration GNN to self-training framework, showing that more trustworthy pseudo labels can be obtained with the calibrated confidence and further improve the performance. Extensive experiments demonstrate the effectiveness of our proposed model in terms of both calibration and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge