How to Spend Your Oracle Budget: Practical Guidance for Protein Structure Prediction Models

Foundation models for protein structure prediction remain unreliable on certain targets. External oracles can flag and correct these failures, but biological oracles are expensive, making oracle budget a critical constraint. Existing guidance methods, such as FK-steering, DPO, and Best K-of-N sampling, differ in how they spend this budget, yet no systematic comparison exists to guide method selection. To bridge this gap, we benchmark these methods alongside the recently proposed Optimisation Over Outputs (O3), which applies off-the-shelf optimisers within a generative model's latent subspace. We extend the usage of O3 to protein structure prediction models. Overall, our work provides the first practical reference for oracle budget-aware guidance. Our evaluation on two protein targets, calmodulin (1CLL) and E. coli aspartate transcarbamoylase (9EEH), reveals that no single method consistently dominates across all budgets and oracles. Specifically, O3 proves most effective at low oracle budgets, while FK-steering and DPO demonstrate improved performance as the budget increases. We distil these findings into actionable recommendations for practitioners operating under real-world oracle-budget constraints.

Variational Gradient Descent using Local Linear Models

Stein Variational Gradient Descent (SVGD) can transport particles along trajectories that reduce the KL divergence between the target and particle distribution but requires the target score function to compute the update. We introduce a new perspective on SVGD that views it as a local estimator of the reversed KL gradient flow. This perspective inspires us to propose new estimators that use local linear models to achieve the same purpose. The proposed estimators can be computed using only samples from the target and particle distribution without needing the target score function. Our proposed variational gradient estimators utilize local linear models, resulting in computational simplicity while maintaining effectiveness comparable to SVGD in terms of estimation biases. Additionally, we demonstrate that under a mild assumption, the estimation of high-dimensional gradient flow can be translated into a lower-dimensional estimation problem, leading to improved estimation accuracy. We validate our claims with experiments on both simulated and real-world datasets.

Sequential Neural Score Estimation: Likelihood-Free Inference with Conditional Score Based Diffusion Models

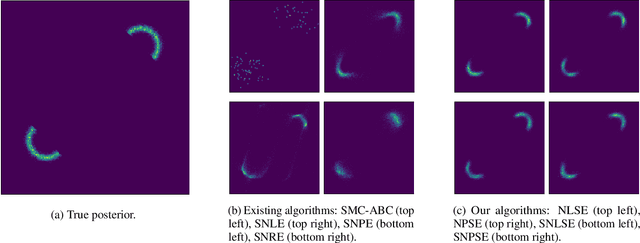
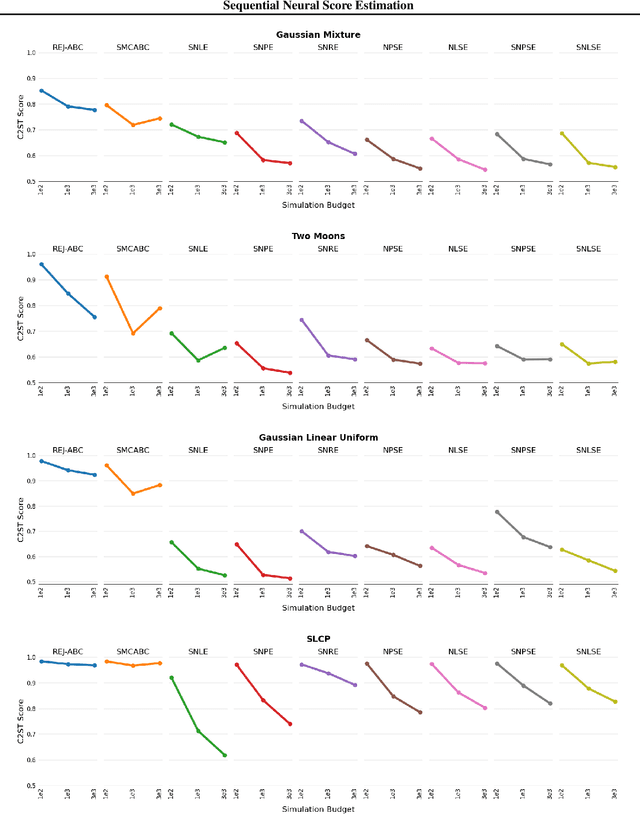
We introduce Sequential Neural Posterior Score Estimation (SNPSE) and Sequential Neural Likelihood Score Estimation (SNLSE), two new score-based methods for Bayesian inference in simulator-based models. Our methods, inspired by the success of score-based methods in generative modelling, leverage conditional score-based diffusion models to generate samples from the posterior distribution of interest. These models can be trained using one of two possible objective functions, one of which approximates the score of the intractable likelihood, while the other directly estimates the score of the posterior. We embed these models into a sequential training procedure, which guides simulations using the current approximation of the posterior at the observation of interest, thereby reducing the simulation cost. We validate our methods, as well as their amortised, non-sequential variants, on several numerical examples, demonstrating comparable or superior performance to existing state-of-the-art methods such as Sequential Neural Posterior Estimation (SNPE) and Sequential Neural Likelihood Estimation (SNLE).