Resource-Efficient Federated Learning

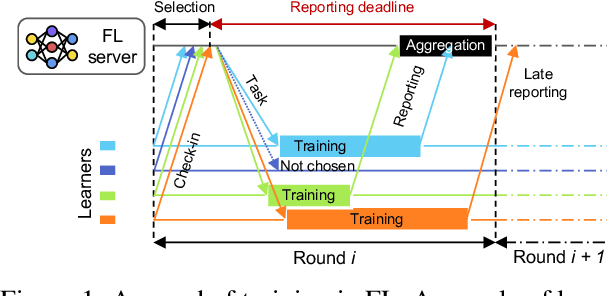
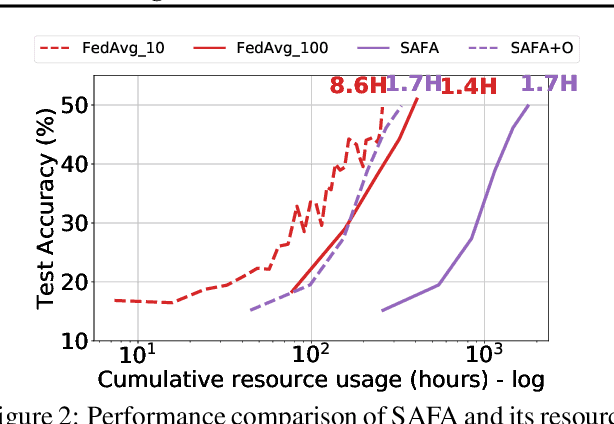
Federated Learning (FL) enables distributed training by learners using local data, thereby enhancing privacy and reducing communication. However, it presents numerous challenges relating to the heterogeneity of the data distribution, device capabilities, and participant availability as deployments scale, which can impact both model convergence and bias. Existing FL schemes use random participant selection to improve fairness; however, this can result in inefficient use of resources and lower quality training. In this work, we systematically address the question of resource efficiency in FL, showing the benefits of intelligent participant selection, and incorporation of updates from straggling participants. We demonstrate how these factors enable resource efficiency while also improving trained model quality.

Rethinking gradient sparsification as total error minimization

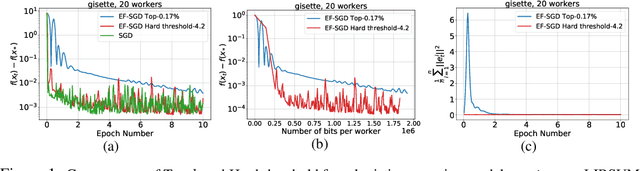
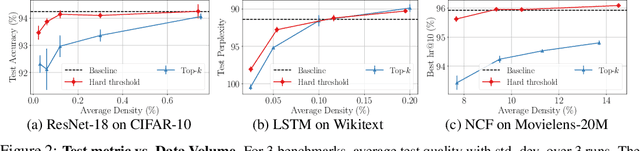
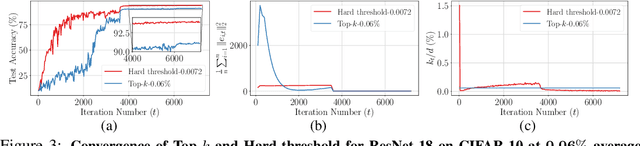
Gradient compression is a widely-established remedy to tackle the communication bottleneck in distributed training of large deep neural networks (DNNs). Under the error-feedback framework, Top-$k$ sparsification, sometimes with $k$ as little as $0.1\%$ of the gradient size, enables training to the same model quality as the uncompressed case for a similar iteration count. From the optimization perspective, we find that Top-$k$ is the communication-optimal sparsifier given a per-iteration $k$ element budget. We argue that to further the benefits of gradient sparsification, especially for DNNs, a different perspective is necessary -- one that moves from per-iteration optimality to consider optimality for the entire training. We identify that the total error -- the sum of the compression errors for all iterations -- encapsulates sparsification throughout training. Then, we propose a communication complexity model that minimizes the total error under a communication budget for the entire training. We find that the hard-threshold sparsifier, a variant of the Top-$k$ sparsifier with $k$ determined by a constant hard-threshold, is the optimal sparsifier for this model. Motivated by this, we provide convex and non-convex convergence analyses for the hard-threshold sparsifier with error-feedback. Unlike with Top-$k$ sparsifier, we show that hard-threshold has the same asymptotic convergence and linear speedup property as SGD in the convex case and has no impact on the data-heterogeneity in the non-convex case. Our diverse experiments on various DNNs and a logistic regression model demonstrated that the hard-threshold sparsifier is more communication-efficient than Top-$k$.

On the Discrepancy between the Theoretical Analysis and Practical Implementations of Compressed Communication for Distributed Deep Learning

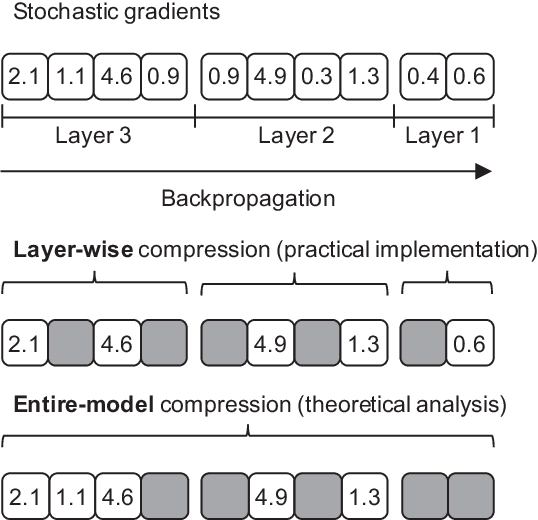
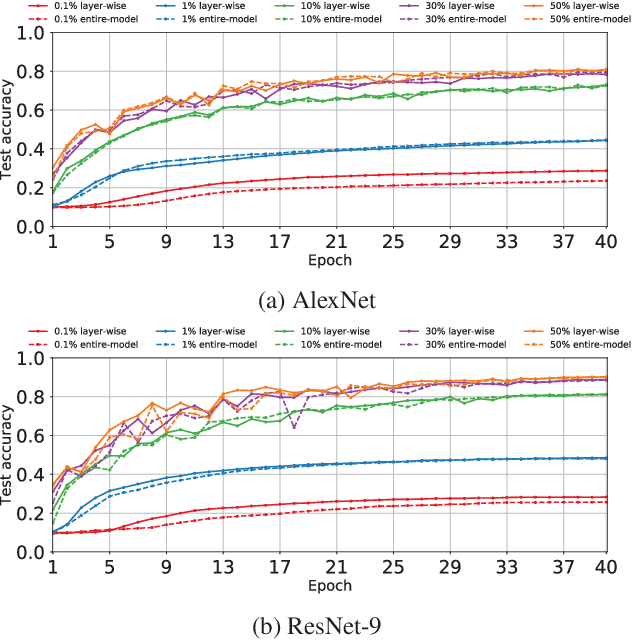
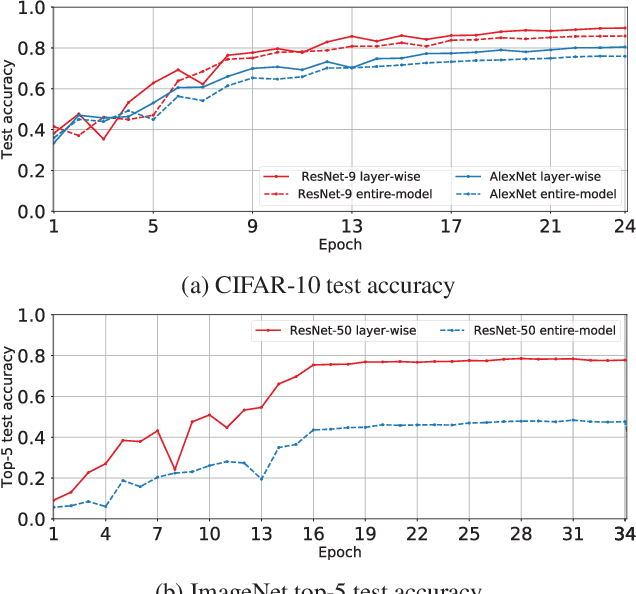
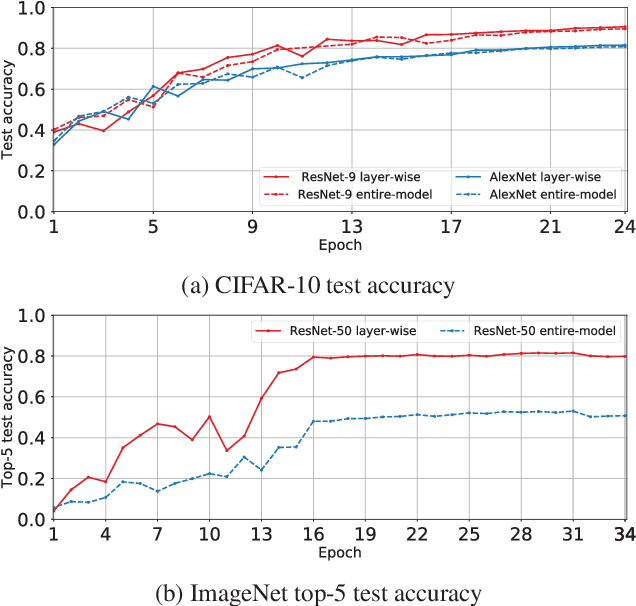
Compressed communication, in the form of sparsification or quantization of stochastic gradients, is employed to reduce communication costs in distributed data-parallel training of deep neural networks. However, there exists a discrepancy between theory and practice: while theoretical analysis of most existing compression methods assumes compression is applied to the gradients of the entire model, many practical implementations operate individually on the gradients of each layer of the model. In this paper, we prove that layer-wise compression is, in theory, better, because the convergence rate is upper bounded by that of entire-model compression for a wide range of biased and unbiased compression methods. However, despite the theoretical bound, our experimental study of six well-known methods shows that convergence, in practice, may or may not be better, depending on the actual trained model and compression ratio. Our findings suggest that it would be advantageous for deep learning frameworks to include support for both layer-wise and entire-model compression.

Natural Compression for Distributed Deep Learning

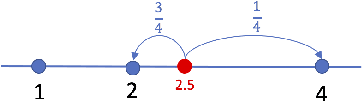
Due to their hunger for big data, modern deep learning models are trained in parallel, often in distributed environments, where communication of model updates is the bottleneck. Various update compression (e.g., quantization, sparsification, dithering) techniques have been proposed in recent years as a successful tool to alleviate this problem. In this work, we introduce a new, remarkably simple and theoretically and practically effective compression technique, which we call natural compression (NC). Our technique is applied individually to all entries of the to-be-compressed update vector and works by randomized rounding to the nearest (negative or positive) power of two. NC is "natural" since the nearest power of two of a real expressed as a float can be obtained without any computation, simply by ignoring the mantissa. We show that compared to no compression, NC increases the second moment of the compressed vector by the tiny factor 9/8 only, which means that the effect of NC on the convergence speed of popular training algorithms, such as distributed SGD, is negligible. However, the communications savings enabled by NC are substantial, leading to 3-4x improvement in overall theoretical running time. For applications requiring more aggressive compression, we generalize NC to natural dithering, which we prove is exponentially better than the immensely popular random dithering technique. Our compression operators can be used on their own or in combination with existing operators for a more aggressive combined effect. Finally, we show that N is particularly effective for the in-network aggregation (INA) framework for distributed training, where the update aggregation is done on a switch, which can only perform integer computations.