Testing Closeness With Unequal Sized Samples
Paper and Code
Apr 17, 2015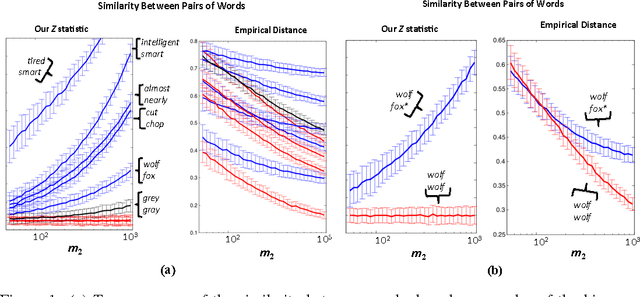
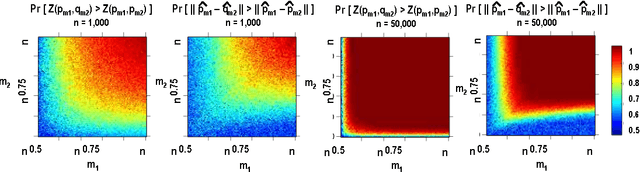
We consider the problem of closeness testing for two discrete distributions in the practically relevant setting of \emph{unequal} sized samples drawn from each of them. Specifically, given a target error parameter $\varepsilon > 0$, $m_1$ independent draws from an unknown distribution $p,$ and $m_2$ draws from an unknown distribution $q$, we describe a test for distinguishing the case that $p=q$ from the case that $||p-q||_1 \geq \varepsilon$. If $p$ and $q$ are supported on at most $n$ elements, then our test is successful with high probability provided $m_1\geq n^{2/3}/\varepsilon^{4/3}$ and $m_2 = \Omega(\max\{\frac{n}{\sqrt m_1\varepsilon^2}, \frac{\sqrt n}{\varepsilon^2}\});$ we show that this tradeoff is optimal throughout this range, to constant factors. These results extend the recent work of Chan et al. who established the sample complexity when the two samples have equal sizes, and tightens the results of Acharya et al. by polynomials factors in both $n$ and $\varepsilon$. As a consequence, we obtain an algorithm for estimating the mixing time of a Markov chain on $n$ states up to a $\log n$ factor that uses $\tilde{O}(n^{3/2} \tau_{mix})$ queries to a "next node" oracle, improving upon the $\tilde{O}(n^{5/3}\tau_{mix})$ query algorithm of Batu et al. Finally, we note that the core of our testing algorithm is a relatively simple statistic that seems to perform well in practice, both on synthetic data and on natural language data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge