A New Perspective On Denoising Based On Optimal Transport

In the standard formulation of the denoising problem, one is given a probabilistic model relating a latent variable $\Theta \in \Omega \subset \mathbb{R}^m \; (m\ge 1)$ and an observation $Z \in \mathbb{R}^d$ according to: $Z \mid \Theta \sim p(\cdot\mid \Theta)$ and $\Theta \sim G^*$, and the goal is to construct a map to recover the latent variable from the observation. The posterior mean, a natural candidate for estimating $\Theta$ from $Z$, attains the minimum Bayes risk (under the squared error loss) but at the expense of over-shrinking the $Z$, and in general may fail to capture the geometric features of the prior distribution $G^*$ (e.g., low dimensionality, discreteness, sparsity, etc.). To rectify these drawbacks, in this paper we take a new perspective on this denoising problem that is inspired by optimal transport (OT) theory and use it to propose a new OT-based denoiser at the population level setting. We rigorously prove that, under general assumptions on the model, our OT-based denoiser is well-defined and unique, and is closely connected to solutions to a Monge OT problem. We then prove that, under appropriate identifiability assumptions on the model, our OT-based denoiser can be recovered solely from information of the marginal distribution of $Z$ and the posterior mean of the model, after solving a linear relaxation problem over a suitable space of couplings that is reminiscent of a standard multimarginal OT (MOT) problem. In particular, thanks to Tweedie's formula, when the likelihood model $\{ p(\cdot \mid \theta) \}_{\theta \in \Omega}$ is an exponential family of distributions, the OT-based denoiser can be recovered solely from the marginal distribution of $Z$. In general, our family of OT-like relaxations is of interest in its own right and for the denoising problem suggests alternative numerical methods inspired by the rich literature on computational OT.

A Mean Field Approach to Empirical Bayes Estimation in High-dimensional Linear Regression

We study empirical Bayes estimation in high-dimensional linear regression. To facilitate computationally efficient estimation of the underlying prior, we adopt a variational empirical Bayes approach, introduced originally in Carbonetto and Stephens (2012) and Kim et al. (2022). We establish asymptotic consistency of the nonparametric maximum likelihood estimator (NPMLE) and its (computable) naive mean field variational surrogate under mild assumptions on the design and the prior. Assuming, in addition, that the naive mean field approximation has a dominant optimizer, we develop a computationally efficient approximation to the oracle posterior distribution, and establish its accuracy under the 1-Wasserstein metric. This enables computationally feasible Bayesian inference; e.g., construction of posterior credible intervals with an average coverage guarantee, Bayes optimal estimation for the regression coefficients, estimation of the proportion of non-nulls, etc. Our analysis covers both deterministic and random designs, and accommodates correlations among the features. To the best of our knowledge, this provides the first rigorous nonparametric empirical Bayes method in a high-dimensional regression setting without sparsity.

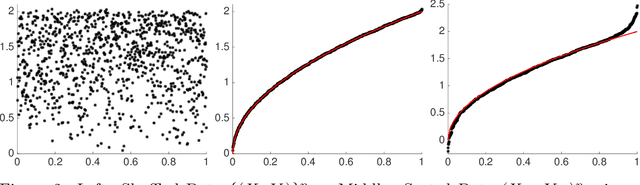
Permuted and Unlinked Monotone Regression in $\mathbb{R}^d$: an approach based on mixture modeling and optimal transport

Suppose that we have a regression problem with response variable Y in $\mathbb{R}^d$ and predictor X in $\mathbb{R}^d$, for $d \geq 1$. In permuted or unlinked regression we have access to separate unordered data on X and Y, as opposed to data on (X,Y)-pairs in usual regression. So far in the literature the case $d=1$ has received attention, see e.g., the recent papers by Rigollet and Weed [Information & Inference, 8, 619--717] and Balabdaoui et al. [J. Mach. Learn. Res., 22(172), 1--60]. In this paper, we consider the general multivariate setting with $d \geq 1$. We show that the notion of cyclical monotonicity of the regression function is sufficient for identification and estimation in the permuted/unlinked regression model. We study permutation recovery in the permuted regression setting and develop a computationally efficient and easy-to-use algorithm for denoising based on the Kiefer-Wolfowitz [Ann. Math. Statist., 27, 887--906] nonparametric maximum likelihood estimator and techniques from the theory of optimal transport. We provide explicit upper bounds on the associated mean squared denoising error for Gaussian noise. As in previous work on the case $d = 1$, the permuted/unlinked setting involves slow (logarithmic) rates of convergence rooting in the underlying deconvolution problem. Numerical studies corroborate our theoretical analysis and show that the proposed approach performs at least on par with the methods in the aforementioned prior work in the case $d = 1$ while achieving substantial reductions in terms of computational complexity.

Rates of Estimation of Optimal Transport Maps using Plug-in Estimators via Barycentric Projections

Optimal transport maps between two probability distributions $\mu$ and $\nu$ on $\mathbb{R}^d$ have found extensive applications in both machine learning and statistics. In practice, these maps need to be estimated from data sampled according to $\mu$ and $\nu$. Plug-in estimators are perhaps most popular in estimating transport maps in the field of computational optimal transport. In this paper, we provide a comprehensive analysis of the rates of convergences for general plug-in estimators defined via barycentric projections. Our main contribution is a new stability estimate for barycentric projections which proceeds under minimal smoothness assumptions and can be used to analyze general plug-in estimators. We illustrate the usefulness of this stability estimate by first providing rates of convergence for the natural discrete-discrete and semi-discrete estimators of optimal transport maps. We then use the same stability estimate to show that, under additional smoothness assumptions of Besov type or Sobolev type, wavelet based or kernel smoothed plug-in estimators respectively speed up the rates of convergence and significantly mitigate the curse of dimensionality suffered by the natural discrete-discrete/semi-discrete estimators. As a by-product of our analysis, we also obtain faster rates of convergence for plug-in estimators of $W_2(\mu,\nu)$, the Wasserstein distance between $\mu$ and $\nu$, under the aforementioned smoothness assumptions, thereby complementing recent results in Chizat et al. (2020). Finally, we illustrate the applicability of our results in obtaining rates of convergence for Wasserstein barycenters between two probability distributions and obtaining asymptotic detection thresholds for some recent optimal-transport based tests of independence.

Convex Regression in Multidimensions: Suboptimality of Least Squares Estimators

The least squares estimator (LSE) is shown to be suboptimal in squared error loss in the usual nonparametric regression model with Gaussian errors for $d \geq 5$ for each of the following families of functions: (i) convex functions supported on a polytope (in fixed design), (ii) bounded convex functions supported on a polytope (in random design), and (iii) convex Lipschitz functions supported on any convex domain (in random design). For each of these families, the risk of the LSE is proved to be of the order $n^{-2/d}$ (up to logarithmic factors) while the minimax risk is $n^{-4/(d+4)}$, for $d \ge 5$. In addition, the first rate of convergence results (worst case and adaptive) for the full convex LSE are established for polytopal domains for all $d \geq 1$. Some new metric entropy results for convex functions are also proved which are of independent interest.

Multivariate extensions of isotonic regression and total variation denoising via entire monotonicity and Hardy-Krause variation

We consider the problem of nonparametric regression when the covariate is $d$-dimensional, where $d \geq 1$. In this paper we introduce and study two nonparametric least squares estimators (LSEs) in this setting---the entirely monotonic LSE and the constrained Hardy-Krause variation LSE. We show that these two LSEs are natural generalizations of univariate isotonic regression and univariate total variation denoising, respectively, to multiple dimensions. We discuss the characterization and computation of these two LSEs obtained from $n$ data points. We provide a detailed study of their risk properties under the squared error loss and fixed uniform lattice design. We show that the finite sample risk of these LSEs is always bounded from above by $n^{-2/3}$ modulo logarithmic factors depending on $d$; thus these nonparametric LSEs avoid the curse of dimensionality to some extent. For the case of the Hardy-Krause variation LSE, we also show that logarithmic factors which increase with $d$ are necessary in the risk upper bound by proving a minimax lower bound. Further, we illustrate that these LSEs are particularly useful in fitting rectangular piecewise constant functions. Specifically, we show that the risk of the entirely monotonic LSE is almost parametric (at most $1/n$ up to logarithmic factors) when the true function is well-approximable by a rectangular piecewise constant entirely monotone function with not too many constant pieces. A similar result is also shown to hold for the constrained Hardy-Krause variation LSE for a simple subclass of rectangular piecewise constant functions. We believe that the proposed LSEs yield a novel approach to estimating multivariate functions using convex optimization that avoid the curse of dimensionality to some extent.

Nonparametric Shape-restricted Regression

We consider the problem of nonparametric regression under shape constraints. The main examples include isotonic regression (with respect to any partial order), unimodal/convex regression, additive shape-restricted regression, and constrained single index model. We review some of the theoretical properties of the least squares estimator (LSE) in these problems, emphasizing on the adaptive nature of the LSE. In particular, we study the behavior of the risk of the LSE, and its pointwise limiting distribution theory, with special emphasis to isotonic regression. We survey various methods for constructing pointwise confidence intervals around these shape-restricted functions. We also briefly discuss the computation of the LSE and indicate some open research problems and future directions.

Covering Numbers for Convex Functions

In this paper we study the covering numbers of the space of convex and uniformly bounded functions in multi-dimension. We find optimal upper and lower bounds for the $\epsilon$-covering number of $\C([a, b]^d, B)$, in the $L_p$-metric, $1 \le p < \infty$, in terms of the relevant constants, where $d \geq 1$, $a < b \in \mathbb{R}$, $B>0$, and $\C([a,b]^d, B)$ denotes the set of all convex functions on $[a, b]^d$ that are uniformly bounded by $B$. We summarize previously known results on covering numbers for convex functions and also provide alternate proofs of some known results. Our results have direct implications in the study of rates of convergence of empirical minimization procedures as well as optimal convergence rates in the numerous convexity constrained function estimation problems.