Data-aware customization of activation functions reduces neural network error

Activation functions play critical roles in neural networks, yet current off-the-shelf neural networks pay little attention to the specific choice of activation functions used. Here we show that data-aware customization of activation functions can result in striking reductions in neural network error. We first give a simple linear algebraic explanation of the role of activation functions in neural networks; then, through connection with the Diaconis-Shahshahani Approximation Theorem, we propose a set of criteria for good activation functions. As a case study, we consider regression tasks with a partially exchangeable target function, \emph{i.e.} $f(u,v,w)=f(v,u,w)$ for $u,v\in \mathbb{R}^d$ and $w\in \mathbb{R}^k$, and prove that for such a target function, using an even activation function in at least one of the layers guarantees that the prediction preserves partial exchangeability for best performance. Since even activation functions are seldom used in practice, we designed the ``seagull'' even activation function $\log(1+x^2)$ according to our criteria. Empirical testing on over two dozen 9-25 dimensional examples with different local smoothness, curvature, and degree of exchangeability revealed that a simple substitution with the ``seagull'' activation function in an already-refined neural network can lead to an order-of-magnitude reduction in error. This improvement was most pronounced when the activation function substitution was applied to the layer in which the exchangeable variables are connected for the first time. While the improvement is greatest for low-dimensional data, experiments on the CIFAR10 image classification dataset showed that use of ``seagull'' can reduce error even for high-dimensional cases. These results collectively highlight the potential of customizing activation functions as a general approach to improve neural network performance.

$Ae^2I$: A Double Autoencoder for Imputation of Missing Values

The most common strategy of imputing missing values in a table is to study either the column-column relationship or the row-row relationship of the data table, then use the relationship to impute the missing values based on the non-missing values from other columns of the same row, or from the other rows of the same column. This paper introduces a double autoencoder for imputation ($Ae^2I$) that simultaneously and collaboratively uses both row-row relationship and column-column relationship to impute the missing values. Empirical tests on Movielens 1M dataset demonstrated that $Ae^2I$ outperforms the current state-of-the-art models for recommender systems by a significant margin.

Predicting Material Properties Using a 3D Graph Neural Network with Invariant Local Descriptors

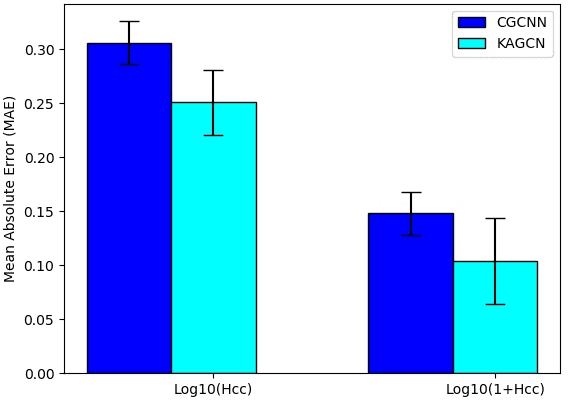
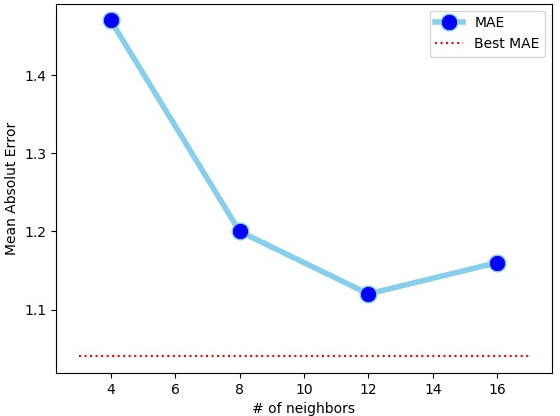
Accurately predicting material properties is critical for discovering and designing novel materials. Machine learning technologies have attracted significant attention in materials science community for their potential for large-scale screening. Among the machine learning methods, graph convolution neural networks (GCNNs) have been one of the most successful ones because of their flexibility and effectiveness in describing 3D structural data. Most existing GCNN models focus on the topological structure but overly simplify the three-dimensional geometric structure. In materials science, the 3D-spatial distribution of the atoms, however, is crucial for determining the atomic states and interatomic forces. In this paper, we propose an adaptive GCNN with novel convolutions that model interactions among all neighboring atoms in three-dimensional space simultaneously. We apply the model to two distinctly challenging problems on predicting material properties. The first is Henry's constant for gas adsorption in Metal-Organic Frameworks (MOFs), which is notoriously difficult because of its high sensitivity to atomic configurations. The second is the ion conductivity of solid-state crystal materials, which is difficult because of very few labeled data available for training. The new model outperforms existing GCNN models on both data sets, suggesting that some important three-dimensional geometric information is indeed captured by the new model.

A Use of Even Activation Functions in Neural Networks

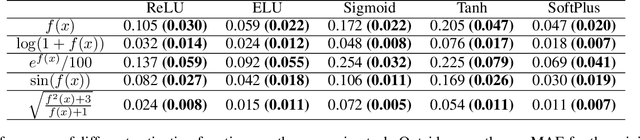
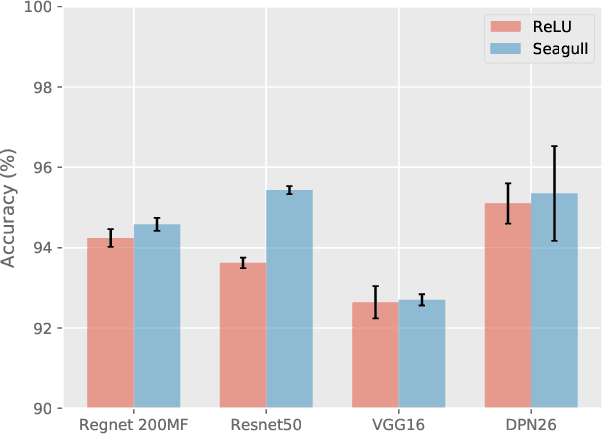
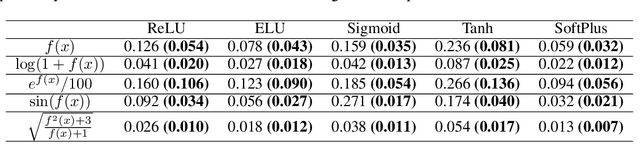
Despite broad interest in applying deep learning techniques to scientific discovery, learning interpretable formulas that accurately describe scientific data is very challenging because of the vast landscape of possible functions and the "black box" nature of deep neural networks. The key to success is to effectively integrate existing knowledge or hypotheses about the underlying structure of the data into the architecture of deep learning models to guide machine learning. Currently, such integration is commonly done through customization of the loss functions. Here we propose an alternative approach to integrate existing knowledge or hypotheses of data structure by constructing custom activation functions that reflect this structure. Specifically, we study a common case when the multivariate target function $f$ to be learned from the data is partially exchangeable, \emph{i.e.} $f(u,v,w)=f(v,u,w)$ for $u,v\in \mathbb{R}^d$. For instance, these conditions are satisfied for the classification of images that is invariant under left-right flipping. Through theoretical proof and experimental verification, we show that using an even activation function in one of the fully connected layers improves neural network performance. In our experimental 9-dimensional regression problems, replacing one of the non-symmetric activation functions with the designated "Seagull" activation function $\log(1+x^2)$ results in substantial improvement in network performance. Surprisingly, even activation functions are seldom used in neural networks. Our results suggest that customized activation functions have great potential in neural networks.

Convex Regression in Multidimensions: Suboptimality of Least Squares Estimators

The least squares estimator (LSE) is shown to be suboptimal in squared error loss in the usual nonparametric regression model with Gaussian errors for $d \geq 5$ for each of the following families of functions: (i) convex functions supported on a polytope (in fixed design), (ii) bounded convex functions supported on a polytope (in random design), and (iii) convex Lipschitz functions supported on any convex domain (in random design). For each of these families, the risk of the LSE is proved to be of the order $n^{-2/d}$ (up to logarithmic factors) while the minimax risk is $n^{-4/(d+4)}$, for $d \ge 5$. In addition, the first rate of convergence results (worst case and adaptive) for the full convex LSE are established for polytopal domains for all $d \geq 1$. Some new metric entropy results for convex functions are also proved which are of independent interest.