MARS via LASSO

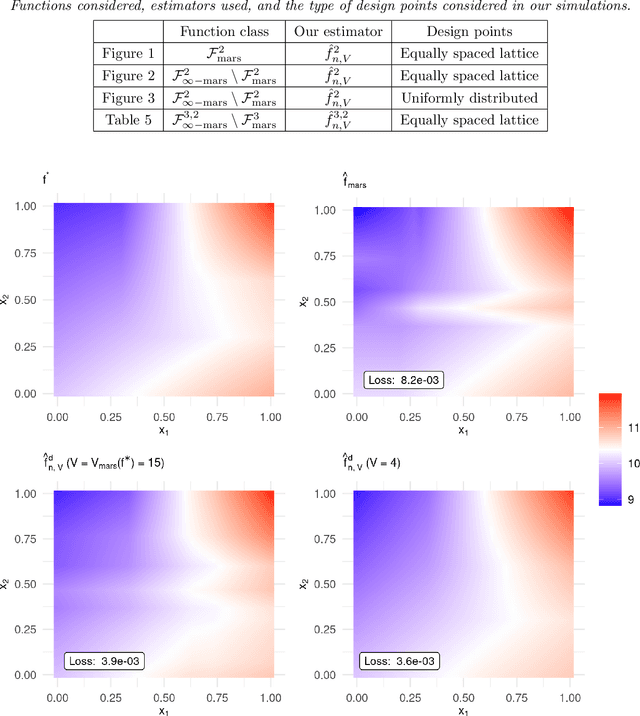
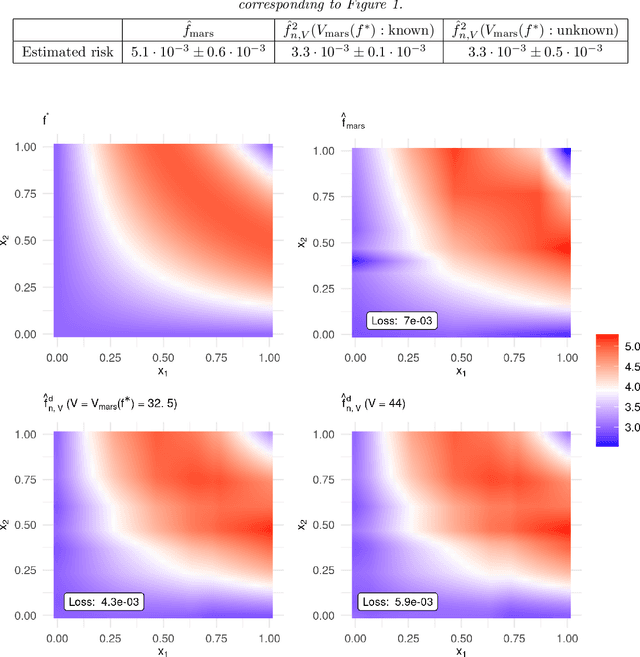
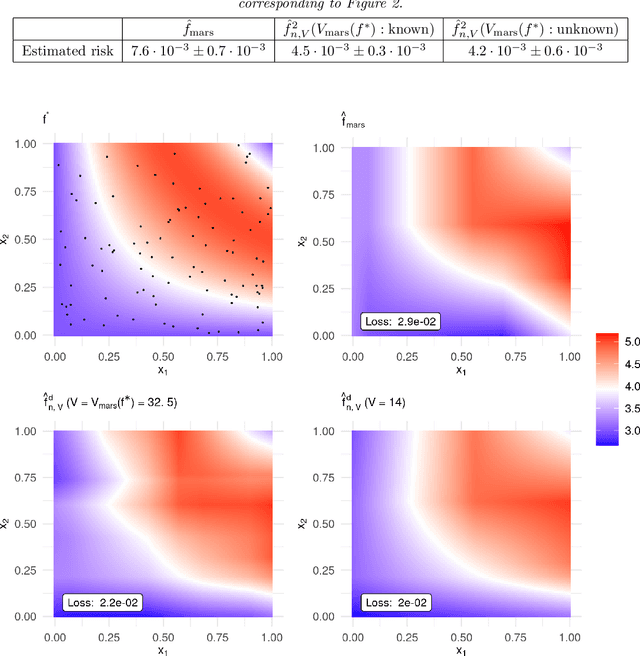
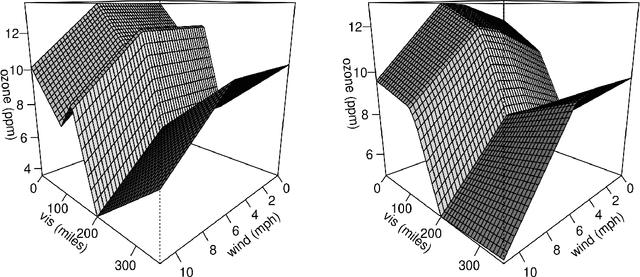
MARS is a popular method for nonparametric regression introduced by Friedman in 1991. MARS fits simple nonlinear and non-additive functions to regression data. We propose and study a natural LASSO variant of the MARS method. Our method is based on least squares estimation over a convex class of functions obtained by considering infinite-dimensional linear combinations of functions in the MARS basis and imposing a variation based complexity constraint. We show that our estimator can be computed via finite-dimensional convex optimization and that it is naturally connected to nonparametric function estimation techniques based on smoothness constraints. Under a simple design assumption, we prove that our estimator achieves a rate of convergence that depends only logarithmically on dimension and thus avoids the usual curse of dimensionality to some extent. We implement our method with a cross-validation scheme for the selection of the involved tuning parameter and show that it has favorable performance compared to the usual MARS method in simulation and real data settings.

On Suboptimality of Least Squares with Application to Estimation of Convex Bodies

We develop a technique for establishing lower bounds on the sample complexity of Least Squares (or, Empirical Risk Minimization) for large classes of functions. As an application, we settle an open problem regarding optimality of Least Squares in estimating a convex set from noisy support function measurements in dimension $d\geq 6$. Specifically, we establish that Least Squares is mimimax sub-optimal, and achieves a rate of $\tilde{\Theta}_d(n^{-2/(d-1)})$ whereas the minimax rate is $\Theta_d(n^{-4/(d+3)})$.

Convex Regression in Multidimensions: Suboptimality of Least Squares Estimators

The least squares estimator (LSE) is shown to be suboptimal in squared error loss in the usual nonparametric regression model with Gaussian errors for $d \geq 5$ for each of the following families of functions: (i) convex functions supported on a polytope (in fixed design), (ii) bounded convex functions supported on a polytope (in random design), and (iii) convex Lipschitz functions supported on any convex domain (in random design). For each of these families, the risk of the LSE is proved to be of the order $n^{-2/d}$ (up to logarithmic factors) while the minimax risk is $n^{-4/(d+4)}$, for $d \ge 5$. In addition, the first rate of convergence results (worst case and adaptive) for the full convex LSE are established for polytopal domains for all $d \geq 1$. Some new metric entropy results for convex functions are also proved which are of independent interest.

Max-Affine Regression: Provable, Tractable, and Near-Optimal Statistical Estimation

Max-affine regression refers to a model where the unknown regression function is modeled as a maximum of $k$ unknown affine functions for a fixed $k \geq 1$. This generalizes linear regression and (real) phase retrieval, and is closely related to convex regression. Working within a non-asymptotic framework, we study this problem in the high-dimensional setting assuming that $k$ is a fixed constant, and focus on estimation of the unknown coefficients of the affine functions underlying the model. We analyze a natural alternating minimization (AM) algorithm for the non-convex least squares objective when the design is random. We show that the AM algorithm, when initialized suitably, converges with high probability and at a geometric rate to a small ball around the optimal coefficients. In order to initialize the algorithm, we propose and analyze a combination of a spectral method and a random search scheme in a low-dimensional space, which may be of independent interest. The final rate that we obtain is near-parametric and minimax optimal (up to a poly-logarithmic factor) as a function of the dimension, sample size, and noise variance. In that sense, our approach should be viewed as a direct and implementable method of enforcing regularization to alleviate the curse of dimensionality in problems of the convex regression type. As a by-product of our analysis, we also obtain guarantees on a classical algorithm for the phase retrieval problem under considerably weaker assumptions on the design distribution than was previously known. Numerical experiments illustrate the sharpness of our bounds in the various problem parameters.

Multivariate extensions of isotonic regression and total variation denoising via entire monotonicity and Hardy-Krause variation

We consider the problem of nonparametric regression when the covariate is $d$-dimensional, where $d \geq 1$. In this paper we introduce and study two nonparametric least squares estimators (LSEs) in this setting---the entirely monotonic LSE and the constrained Hardy-Krause variation LSE. We show that these two LSEs are natural generalizations of univariate isotonic regression and univariate total variation denoising, respectively, to multiple dimensions. We discuss the characterization and computation of these two LSEs obtained from $n$ data points. We provide a detailed study of their risk properties under the squared error loss and fixed uniform lattice design. We show that the finite sample risk of these LSEs is always bounded from above by $n^{-2/3}$ modulo logarithmic factors depending on $d$; thus these nonparametric LSEs avoid the curse of dimensionality to some extent. For the case of the Hardy-Krause variation LSE, we also show that logarithmic factors which increase with $d$ are necessary in the risk upper bound by proving a minimax lower bound. Further, we illustrate that these LSEs are particularly useful in fitting rectangular piecewise constant functions. Specifically, we show that the risk of the entirely monotonic LSE is almost parametric (at most $1/n$ up to logarithmic factors) when the true function is well-approximable by a rectangular piecewise constant entirely monotone function with not too many constant pieces. A similar result is also shown to hold for the constrained Hardy-Krause variation LSE for a simple subclass of rectangular piecewise constant functions. We believe that the proposed LSEs yield a novel approach to estimating multivariate functions using convex optimization that avoid the curse of dimensionality to some extent.

Nonparametric Shape-restricted Regression

We consider the problem of nonparametric regression under shape constraints. The main examples include isotonic regression (with respect to any partial order), unimodal/convex regression, additive shape-restricted regression, and constrained single index model. We review some of the theoretical properties of the least squares estimator (LSE) in these problems, emphasizing on the adaptive nature of the LSE. In particular, we study the behavior of the risk of the LSE, and its pointwise limiting distribution theory, with special emphasis to isotonic regression. We survey various methods for constructing pointwise confidence intervals around these shape-restricted functions. We also briefly discuss the computation of the LSE and indicate some open research problems and future directions.

On the nonparametric maximum likelihood estimator for Gaussian location mixture densities with application to Gaussian denoising

We study the Nonparametric Maximum Likelihood Estimator (NPMLE) for estimating Gaussian location mixture densities in $d$-dimensions from independent observations. Unlike usual likelihood-based methods for fitting mixtures, NPMLEs are based on convex optimization. We prove finite sample results on the Hellinger accuracy of every NPMLE. Our results imply, in particular, that every NPMLE achieves near parametric risk (up to logarithmic multiplicative factors) when the true density is a discrete Gaussian mixture without any prior information on the number of mixture components. NPMLEs can naturally be used to yield empirical Bayes estimates of the Oracle Bayes estimator in the Gaussian denoising problem. We prove bounds for the accuracy of the empirical Bayes estimate as an approximation to the Oracle Bayes estimator. Here our results imply that the empirical Bayes estimator performs at nearly the optimal level (up to logarithmic multiplicative factors) for denoising in clustering situations without any prior knowledge of the number of clusters.

Stochastically Transitive Models for Pairwise Comparisons: Statistical and Computational Issues

There are various parametric models for analyzing pairwise comparison data, including the Bradley-Terry-Luce (BTL) and Thurstone models, but their reliance on strong parametric assumptions is limiting. In this work, we study a flexible model for pairwise comparisons, under which the probabilities of outcomes are required only to satisfy a natural form of stochastic transitivity. This class includes parametric models including the BTL and Thurstone models as special cases, but is considerably more general. We provide various examples of models in this broader stochastically transitive class for which classical parametric models provide poor fits. Despite this greater flexibility, we show that the matrix of probabilities can be estimated at the same rate as in standard parametric models. On the other hand, unlike in the BTL and Thurstone models, computing the minimax-optimal estimator in the stochastically transitive model is non-trivial, and we explore various computationally tractable alternatives. We show that a simple singular value thresholding algorithm is statistically consistent but does not achieve the minimax rate. We then propose and study algorithms that achieve the minimax rate over interesting sub-classes of the full stochastically transitive class. We complement our theoretical results with thorough numerical simulations.

Sharp Inequalities for $f$-divergences

$f$-divergences are a general class of divergences between probability measures which include as special cases many commonly used divergences in probability, mathematical statistics and information theory such as Kullback-Leibler divergence, chi-squared divergence, squared Hellinger distance, total variation distance etc. In this paper, we study the problem of maximizing or minimizing an $f$-divergence between two probability measures subject to a finite number of constraints on other $f$-divergences. We show that these infinite-dimensional optimization problems can all be reduced to optimization problems over small finite dimensional spaces which are tractable. Our results lead to a comprehensive and unified treatment of the problem of obtaining sharp inequalities between $f$-divergences. We demonstrate that many of the existing results on inequalities between $f$-divergences can be obtained as special cases of our results and we also improve on some existing non-sharp inequalities.

Covering Numbers for Convex Functions

In this paper we study the covering numbers of the space of convex and uniformly bounded functions in multi-dimension. We find optimal upper and lower bounds for the $\epsilon$-covering number of $\C([a, b]^d, B)$, in the $L_p$-metric, $1 \le p < \infty$, in terms of the relevant constants, where $d \geq 1$, $a < b \in \mathbb{R}$, $B>0$, and $\C([a,b]^d, B)$ denotes the set of all convex functions on $[a, b]^d$ that are uniformly bounded by $B$. We summarize previously known results on covering numbers for convex functions and also provide alternate proofs of some known results. Our results have direct implications in the study of rates of convergence of empirical minimization procedures as well as optimal convergence rates in the numerous convexity constrained function estimation problems.