MARS via LASSO

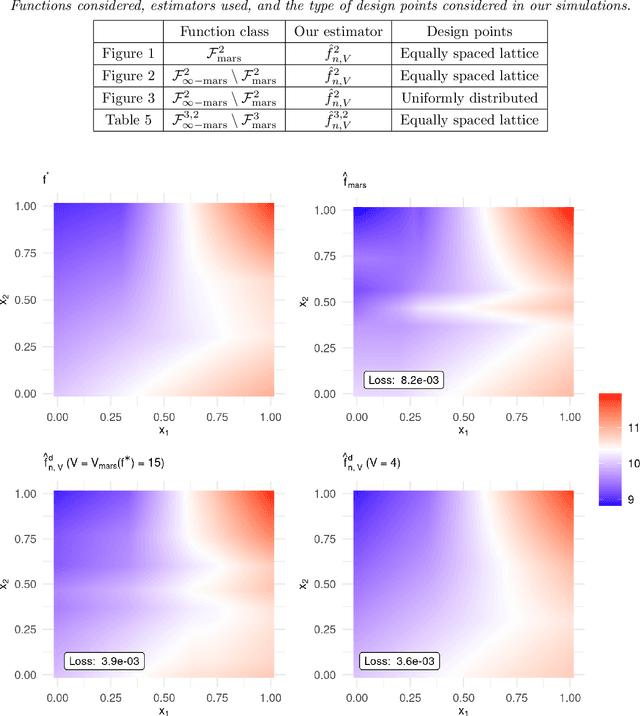
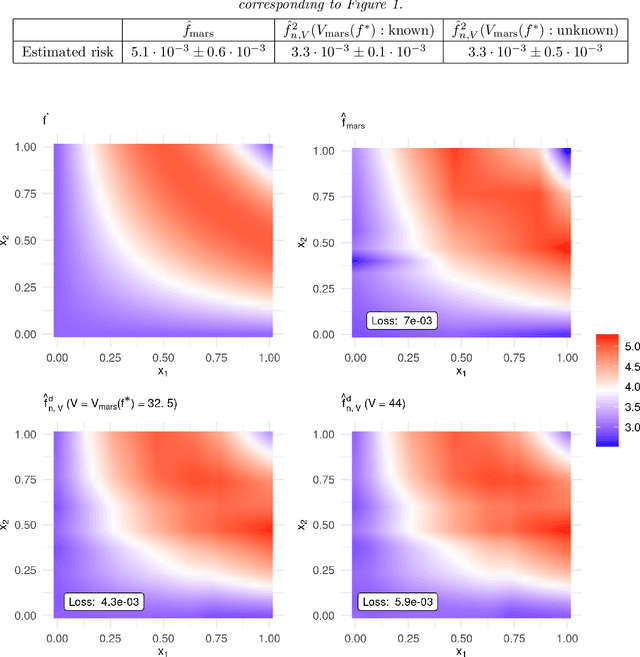
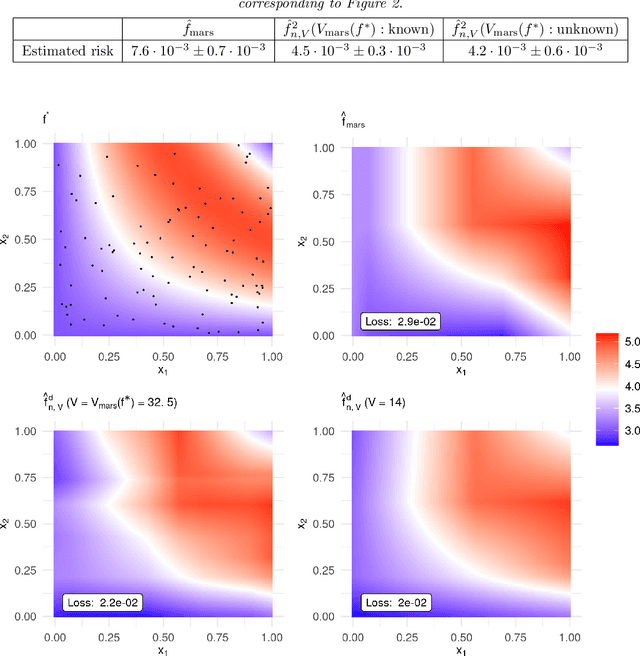
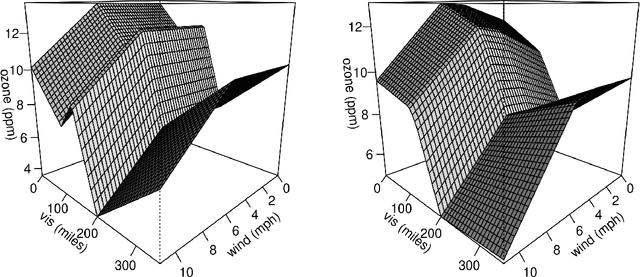
MARS is a popular method for nonparametric regression introduced by Friedman in 1991. MARS fits simple nonlinear and non-additive functions to regression data. We propose and study a natural LASSO variant of the MARS method. Our method is based on least squares estimation over a convex class of functions obtained by considering infinite-dimensional linear combinations of functions in the MARS basis and imposing a variation based complexity constraint. We show that our estimator can be computed via finite-dimensional convex optimization and that it is naturally connected to nonparametric function estimation techniques based on smoothness constraints. Under a simple design assumption, we prove that our estimator achieves a rate of convergence that depends only logarithmically on dimension and thus avoids the usual curse of dimensionality to some extent. We implement our method with a cross-validation scheme for the selection of the involved tuning parameter and show that it has favorable performance compared to the usual MARS method in simulation and real data settings.

Multivariate extensions of isotonic regression and total variation denoising via entire monotonicity and Hardy-Krause variation

We consider the problem of nonparametric regression when the covariate is $d$-dimensional, where $d \geq 1$. In this paper we introduce and study two nonparametric least squares estimators (LSEs) in this setting---the entirely monotonic LSE and the constrained Hardy-Krause variation LSE. We show that these two LSEs are natural generalizations of univariate isotonic regression and univariate total variation denoising, respectively, to multiple dimensions. We discuss the characterization and computation of these two LSEs obtained from $n$ data points. We provide a detailed study of their risk properties under the squared error loss and fixed uniform lattice design. We show that the finite sample risk of these LSEs is always bounded from above by $n^{-2/3}$ modulo logarithmic factors depending on $d$; thus these nonparametric LSEs avoid the curse of dimensionality to some extent. For the case of the Hardy-Krause variation LSE, we also show that logarithmic factors which increase with $d$ are necessary in the risk upper bound by proving a minimax lower bound. Further, we illustrate that these LSEs are particularly useful in fitting rectangular piecewise constant functions. Specifically, we show that the risk of the entirely monotonic LSE is almost parametric (at most $1/n$ up to logarithmic factors) when the true function is well-approximable by a rectangular piecewise constant entirely monotone function with not too many constant pieces. A similar result is also shown to hold for the constrained Hardy-Krause variation LSE for a simple subclass of rectangular piecewise constant functions. We believe that the proposed LSEs yield a novel approach to estimating multivariate functions using convex optimization that avoid the curse of dimensionality to some extent.