MARS via LASSO
Paper and Code
Nov 23, 2021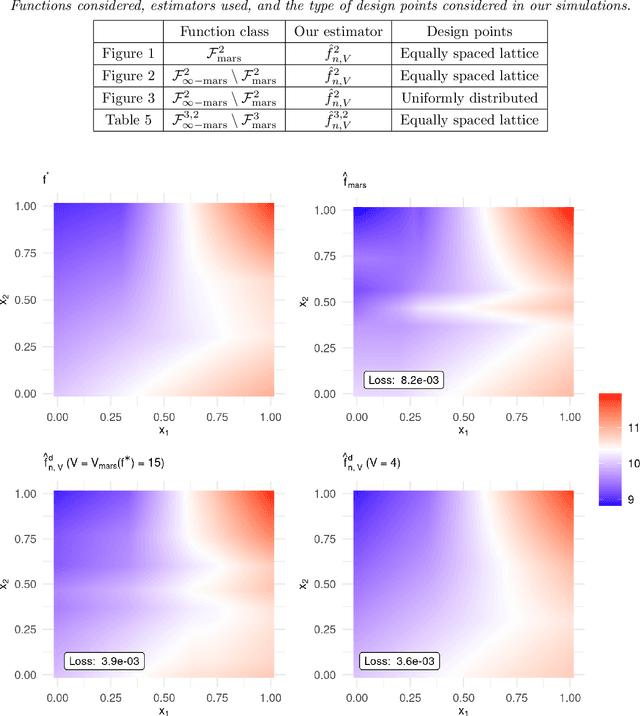
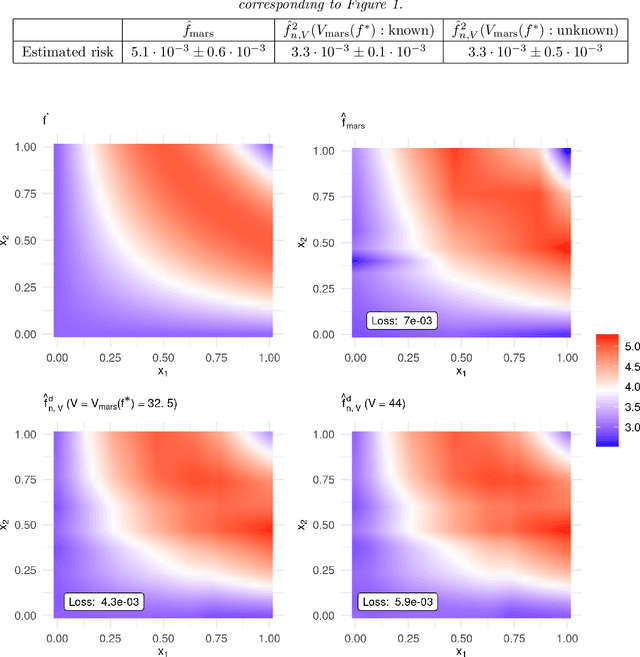
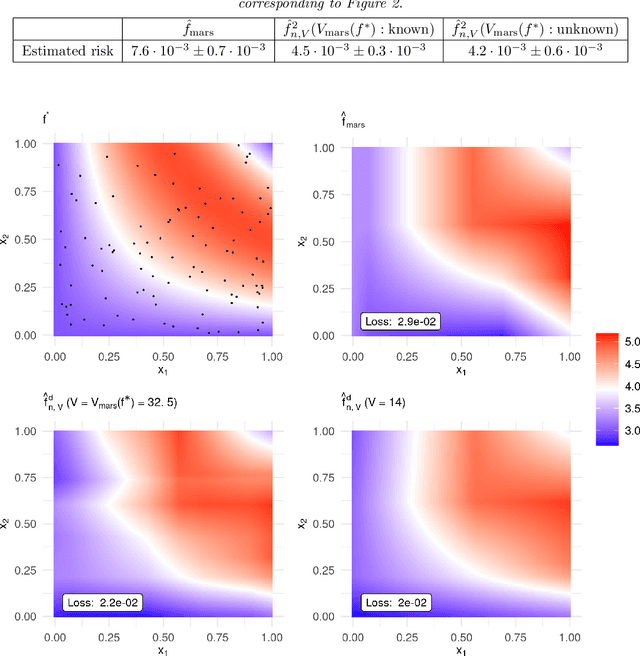
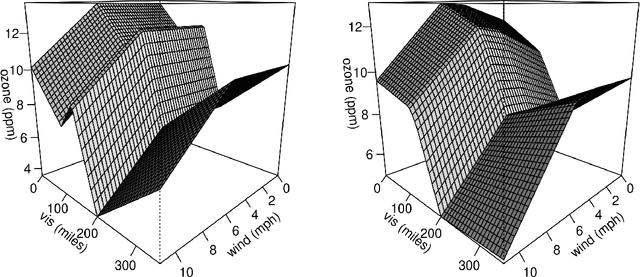
MARS is a popular method for nonparametric regression introduced by Friedman in 1991. MARS fits simple nonlinear and non-additive functions to regression data. We propose and study a natural LASSO variant of the MARS method. Our method is based on least squares estimation over a convex class of functions obtained by considering infinite-dimensional linear combinations of functions in the MARS basis and imposing a variation based complexity constraint. We show that our estimator can be computed via finite-dimensional convex optimization and that it is naturally connected to nonparametric function estimation techniques based on smoothness constraints. Under a simple design assumption, we prove that our estimator achieves a rate of convergence that depends only logarithmically on dimension and thus avoids the usual curse of dimensionality to some extent. We implement our method with a cross-validation scheme for the selection of the involved tuning parameter and show that it has favorable performance compared to the usual MARS method in simulation and real data settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge