Debiased LASSO under Poisson-Gauss Model

Quantifying uncertainty in high-dimensional sparse linear regression is a fundamental task in statistics that arises in various applications. One of the most successful methods for quantifying uncertainty is the debiased LASSO, which has a solid theoretical foundation but is restricted to settings where the noise is purely additive. Motivated by real-world applications, we study the so-called Poisson inverse problem with additive Gaussian noise and propose a debiased LASSO algorithm that only requires $n \gg s\log^2p$ samples, which is optimal up to a logarithmic factor.

On the Variance, Admissibility, and Stability of Empirical Risk Minimization

It is well known that Empirical Risk Minimization (ERM) with squared loss may attain minimax suboptimal error rates (Birg\'e and Massart, 1993). The key message of this paper is that, under mild assumptions, the suboptimality of ERM must be due to large bias rather than variance. More precisely, in the bias-variance decomposition of the squared error of the ERM, the variance term necessarily enjoys the minimax rate. In the case of fixed design, we provide an elementary proof of this fact using the probabilistic method. Then, we prove this result for various models in the random design setting. In addition, we provide a simple proof of Chatterjee's admissibility theorem (Chatterjee, 2014, Theorem 1.4), which states that ERM cannot be ruled out as an optimal method, in the fixed design setting, and extend this result to the random design setting. We also show that our estimates imply stability of ERM, complementing the main result of Caponnetto and Rakhlin (2006) for non-Donsker classes. Finally, we show that for non-Donsker classes, there are functions close to the ERM, yet far from being almost-minimizers of the empirical loss, highlighting the somewhat irregular nature of the loss landscape.

Efficient Minimax Optimal Estimators For Multivariate Convex Regression

We study the computational aspects of the task of multivariate convex regression in dimension $d \geq 5$. We present the first computationally efficient minimax optimal (up to logarithmic factors) estimators for the tasks of (i) $L$-Lipschitz convex regression (ii) $\Gamma$-bounded convex regression under polytopal support. The proof of the correctness of these estimators uses a variety of tools from different disciplines, among them empirical process theory, stochastic geometry, and potential theory. This work is the first to show the existence of efficient minimax optimal estimators for non-Donsker classes that their corresponding Least Squares Estimators are provably minimax sub-optimal; a result of independent interest.

On the Minimal Error of Empirical Risk Minimization

We study the minimal error of the Empirical Risk Minimization (ERM) procedure in the task of regression, both in the random and the fixed design settings. Our sharp lower bounds shed light on the possibility (or impossibility) of adapting to simplicity of the model generating the data. In the fixed design setting, we show that the error is governed by the global complexity of the entire class. In contrast, in random design, ERM may only adapt to simpler models if the local neighborhoods around the regression function are nearly as complex as the class itself, a somewhat counter-intuitive conclusion. We provide sharp lower bounds for performance of ERM for both Donsker and non-Donsker classes. We also discuss our results through the lens of recent studies on interpolation in overparameterized models.

A bounded-noise mechanism for differential privacy

Answering multiple counting queries is one of the best-studied problems in differential privacy. Its goal is to output an approximation of the average $\frac{1}{n}\sum_{i=1}^n \vec{x}^{(i)}$ of vectors $\vec{x}^{(i)} \in [0,1]^k$, while preserving the privacy with respect to any $\vec{x}^{(i)}$. We present an $(\epsilon,\delta)$-private mechanism with optimal $\ell_\infty$ error for most values of $\delta$. This result settles the conjecture of Steinke and Ullman [2020] for the these values of $\delta$. Our algorithm adds independent noise of bounded magnitude to each of the $k$ coordinates, while prior solutions relied on unbounded noise such as the Laplace and Gaussian mechanisms.

On Suboptimality of Least Squares with Application to Estimation of Convex Bodies

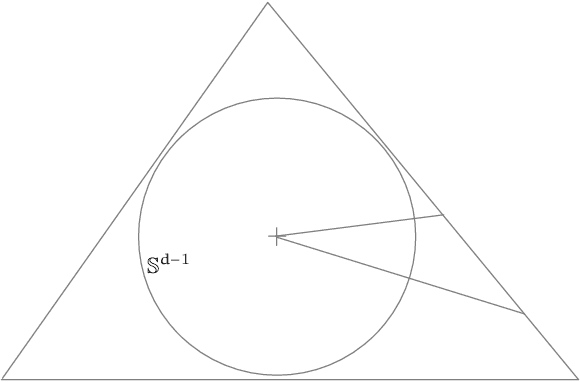
We develop a technique for establishing lower bounds on the sample complexity of Least Squares (or, Empirical Risk Minimization) for large classes of functions. As an application, we settle an open problem regarding optimality of Least Squares in estimating a convex set from noisy support function measurements in dimension $d\geq 6$. Specifically, we establish that Least Squares is mimimax sub-optimal, and achieves a rate of $\tilde{\Theta}_d(n^{-2/(d-1)})$ whereas the minimax rate is $\Theta_d(n^{-4/(d+3)})$.

Convex Regression in Multidimensions: Suboptimality of Least Squares Estimators

The least squares estimator (LSE) is shown to be suboptimal in squared error loss in the usual nonparametric regression model with Gaussian errors for $d \geq 5$ for each of the following families of functions: (i) convex functions supported on a polytope (in fixed design), (ii) bounded convex functions supported on a polytope (in random design), and (iii) convex Lipschitz functions supported on any convex domain (in random design). For each of these families, the risk of the LSE is proved to be of the order $n^{-2/d}$ (up to logarithmic factors) while the minimax risk is $n^{-4/(d+4)}$, for $d \ge 5$. In addition, the first rate of convergence results (worst case and adaptive) for the full convex LSE are established for polytopal domains for all $d \geq 1$. Some new metric entropy results for convex functions are also proved which are of independent interest.

Double descent in the condition number

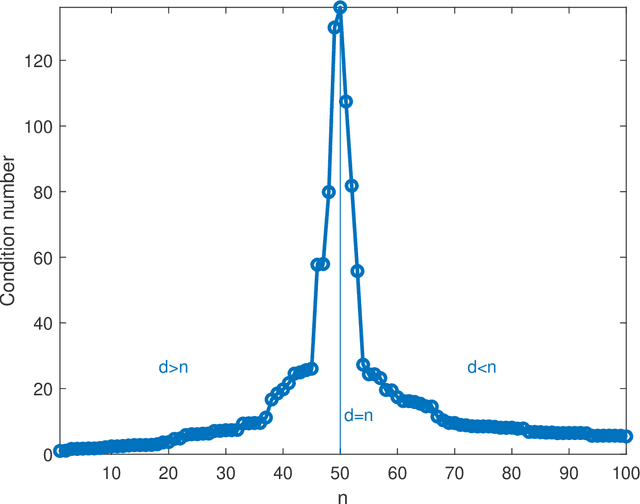
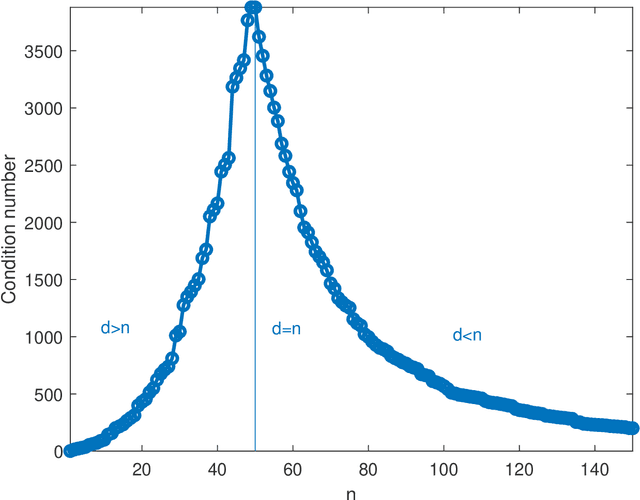
In solving a system of $n$ linear equations in $d$ variables $Ax=b$, the condition number of the $n,d$ matrix $A$ measures how much errors in the data $b$ affect the solution $x$. Bounds of this type are important in many inverse problems. An example is machine learning where the key task is to estimate an underlying function from a set of measurements at random points in a high dimensional space and where low sensitivity to error in the data is a requirement for good predictive performance. Here we discuss the simple observation, which is well-known but surprisingly little quoted that when the columns of $A$ are random vectors, the condition number of $A$ is highest if $d=n$, that is when the inverse of $A$ exists. An overdetermined system ($n>d$) as well as an underdetermined system ($n<d$), for which the pseudoinverse must be used instead of the inverse, typically have significantly better, that is lower, condition numbers. Thus the condition number of $A$ plotted as function of $d$ shows a double descent behavior with a peak at $d=n$.

The Log-Concave Maximum Likelihood Estimator is Optimal in High Dimensions

We study the problem of learning a $d$-dimensional log-concave distribution from $n$ i.i.d. samples with respect to both the squared Hellinger and the total variation distances. We show that for all $d \ge 4$ the maximum likelihood estimator achieves an optimal risk (up to a logarithmic factor) of $O_d(n^{-2/(d+1)}\log(n))$ in terms of squared Hellinger distance. Previously, the optimality of the MLE was known only for $d\le 3$. Additionally, we show that the metric plays a key role, by proving that the minimax risk is at least $\Omega_d(n^{-2/(d+4)})$ in terms of the total variation. Finally, we significantly improve the dimensional constant in the best known lower bound on the risk with respect to the squared Hellinger distance, improving the bound from $2^{-d}n^{-2/(d+1)}$ to $\Omega(n^{-2/(d+1)})$. This implies that estimating a log-concave density up to a fixed accuracy requires a number of samples which is exponential in the dimension.

Space lower bounds for linear prediction

We show that fundamental learning tasks, such as finding an approximate linear separator or linear regression, require memory at least \emph{quadratic} in the dimension, in a natural streaming setting. This implies that such problems cannot be solved (at least in this setting) by scalable memory-efficient streaming algorithms. Our results build on a memory lower bound for a simple linear-algebraic problem -- finding orthogonal vectors -- and utilize the estimates on the packing of the Grassmannian, the manifold of all linear subspaces of fixed dimension.