Double descent in the condition number

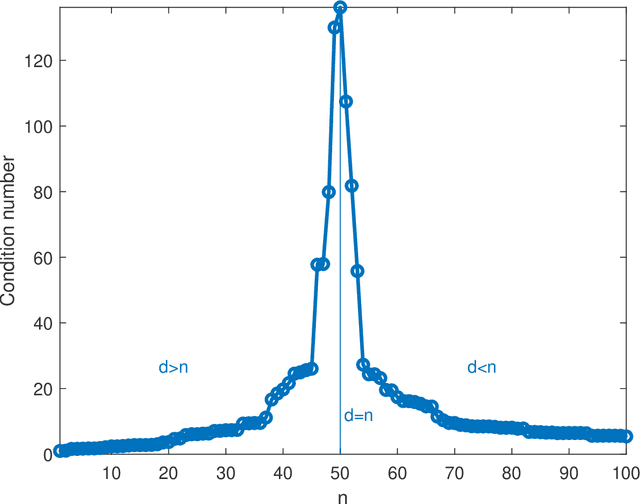
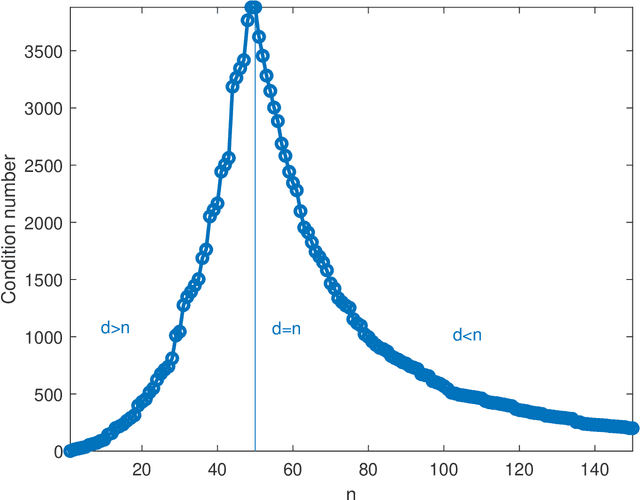
In solving a system of $n$ linear equations in $d$ variables $Ax=b$, the condition number of the $n,d$ matrix $A$ measures how much errors in the data $b$ affect the solution $x$. Bounds of this type are important in many inverse problems. An example is machine learning where the key task is to estimate an underlying function from a set of measurements at random points in a high dimensional space and where low sensitivity to error in the data is a requirement for good predictive performance. Here we discuss the simple observation, which is well-known but surprisingly little quoted that when the columns of $A$ are random vectors, the condition number of $A$ is highest if $d=n$, that is when the inverse of $A$ exists. An overdetermined system ($n>d$) as well as an underdetermined system ($n<d$), for which the pseudoinverse must be used instead of the inverse, typically have significantly better, that is lower, condition numbers. Thus the condition number of $A$ plotted as function of $d$ shows a double descent behavior with a peak at $d=n$.