On Biologically Plausible Learning in Continuous Time

Biological learning unfolds continuously in time, yet most algorithmic models rely on discrete updates and separate inference and learning phases. We study a continuous-time neural model that unifies several biologically plausible learning algorithms and removes the need for phase separation. Rules including stochastic gradient descent (SGD), feedback alignment (FA), direct feedback alignment (DFA), and Kolen-Pollack (KP) emerge naturally as limiting cases of the dynamics. Simulations show that these continuous-time networks stably learn at biological timescales, even under temporal mismatches and integration noise. Through analysis and simulation, we show that learning depends on temporal overlap: a synapse updates correctly only when its input and the corresponding error signal coincide in time. When inputs are held constant, learning strength declines linearly as the delay between input and error approaches the stimulus duration, explaining observed robustness and failure across network depths. Critically, robust learning requires the synaptic plasticity timescale to exceed the stimulus duration by one to two orders of magnitude. For typical cortical stimuli (tens of milliseconds), this places the functional plasticity window in the few-second range, a testable prediction that identifies seconds-scale eligibility traces as necessary for error-driven learning in biological circuits.

LLM-ERM: Sample-Efficient Program Learning via LLM-Guided Search

We seek algorithms for program learning that are both sample-efficient and computationally feasible. Classical results show that targets admitting short program descriptions (e.g., with short ``python code'') can be learned with a ``small'' number of examples (scaling with the size of the code) via length-first program enumeration, but the search is exponential in description length. Consequently, Gradient-based training avoids this cost yet can require exponentially many samples on certain short-program families. To address this gap, we introduce LLM-ERM, a propose-and-verify framework that replaces exhaustive enumeration with an LLM-guided search over candidate programs while retaining ERM-style selection on held-out data. Specifically, we draw $k$ candidates with a pretrained reasoning-augmented LLM, compile and check each on the data, and return the best verified hypothesis, with no feedback, adaptivity, or gradients. Theoretically, we show that coordinate-wise online mini-batch SGD requires many samples to learn certain short programs. {\em Empirically, LLM-ERM solves tasks such as parity variants, pattern matching, and primality testing with as few as 200 samples, while SGD-trained transformers overfit even with 100,000 samples}. These results indicate that language-guided program synthesis recovers much of the statistical efficiency of finite-class ERM while remaining computationally tractable, offering a practical route to learning succinct hypotheses beyond the reach of gradient-based training.

A universal compression theory: Lottery ticket hypothesis and superpolynomial scaling laws

When training large-scale models, the performance typically scales with the number of parameters and the dataset size according to a slow power law. A fundamental theoretical and practical question is whether comparable performance can be achieved with significantly smaller models and substantially less data. In this work, we provide a positive and constructive answer. We prove that a generic permutation-invariant function of $d$ objects can be asymptotically compressed into a function of $\operatorname{polylog} d$ objects with vanishing error. This theorem yields two key implications: (Ia) a large neural network can be compressed to polylogarithmic width while preserving its learning dynamics; (Ib) a large dataset can be compressed to polylogarithmic size while leaving the loss landscape of the corresponding model unchanged. (Ia) directly establishes a proof of the \textit{dynamical} lottery ticket hypothesis, which states that any ordinary network can be strongly compressed such that the learning dynamics and result remain unchanged. (Ib) shows that a neural scaling law of the form $L\sim d^{-\alpha}$ can be boosted to an arbitrarily fast power law decay, and ultimately to $\exp(-\alpha' \sqrt[m]{d})$.

Position: A Theory of Deep Learning Must Include Compositional Sparsity

Overparametrized Deep Neural Networks (DNNs) have demonstrated remarkable success in a wide variety of domains too high-dimensional for classical shallow networks subject to the curse of dimensionality. However, open questions about fundamental principles, that govern the learning dynamics of DNNs, remain. In this position paper we argue that it is the ability of DNNs to exploit the compositionally sparse structure of the target function driving their success. As such, DNNs can leverage the property that most practically relevant functions can be composed from a small set of constituent functions, each of which relies only on a low-dimensional subset of all inputs. We show that this property is shared by all efficiently Turing-computable functions and is therefore highly likely present in all current learning problems. While some promising theoretical insights on questions concerned with approximation and generalization exist in the setting of compositionally sparse functions, several important questions on the learnability and optimization of DNNs remain. Completing the picture of the role of compositional sparsity in deep learning is essential to a comprehensive theory of artificial, and even general, intelligence.

Emergence of Hebbian Dynamics in Regularized Non-Local Learners

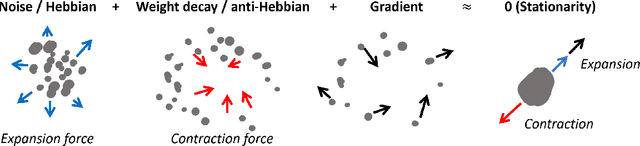
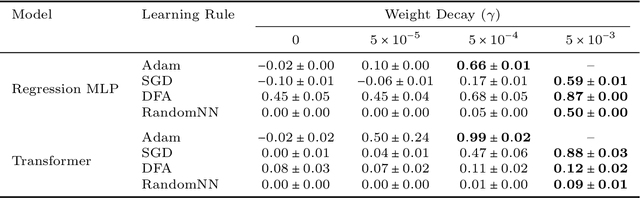
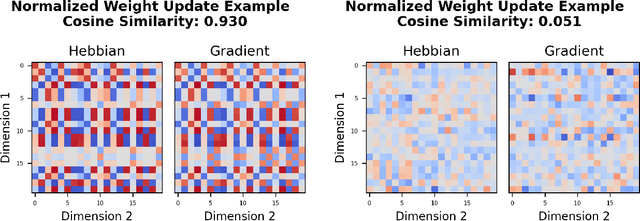
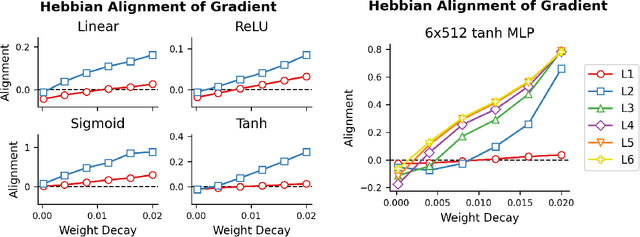
Stochastic Gradient Descent (SGD) has emerged as a remarkably effective learning algorithm, underpinning nearly all state-of-the-art machine learning models, from large language models to autonomous vehicles. Despite its practical success, SGD appears fundamentally distinct from biological learning mechanisms. It is widely believed that the biological brain can not implement gradient descent because it is nonlocal, and we have found little (if any) experimental evidence for it. In contrast, the brain is widely thought to learn via local Hebbian learning principles, which have been seen as incompatible with gradient descent. In this paper, we establish a theoretical and empirical connection between the learning signals of neural networks trained using SGD with weight decay and those trained with Hebbian learning near convergence. We show that SGD with regularization can appear to learn according to a Hebbian rule, and SGD with injected noise according to an anti-Hebbian rule. We also provide empirical evidence that Hebbian learning properties can emerge in a network with weight decay from virtually any learning rule--even random ones. These results may bridge a long-standing gap between artificial and biological learning, revealing Hebbian properties as an epiphenomenon of deeper optimization principles and cautioning against interpreting their presence in neural data as evidence against more complex hetero-synaptic mechanisms.

Heterosynaptic Circuits Are Universal Gradient Machines

We propose a design principle for the learning circuits of the biological brain. The principle states that almost any dendritic weights updated via heterosynaptic plasticity can implement a generalized and efficient class of gradient-based meta-learning. The theory suggests that a broad class of biologically plausible learning algorithms, together with the standard machine learning optimizers, can be grounded in heterosynaptic circuit motifs. This principle suggests that the phenomenology of (anti-) Hebbian (HBP) and heterosynaptic plasticity (HSP) may emerge from the same underlying dynamics, thus providing a unifying explanation. It also suggests an alternative perspective of neuroplasticity, where HSP is promoted to the primary learning and memory mechanism, and HBP is an emergent byproduct. We present simulations that show that (a) HSP can explain the metaplasticity of neurons, (b) HSP can explain the flexibility of the biology circuits, and (c) gradient learning can arise quickly from simple evolutionary dynamics that do not compute any explicit gradient. While our primary focus is on biology, the principle also implies a new approach to designing AI training algorithms and physically learnable AI hardware. Conceptually, our result demonstrates that contrary to the common belief, gradient computation may be extremely easy and common in nature.

Parameter Symmetry Breaking and Restoration Determines the Hierarchical Learning in AI Systems

The dynamics of learning in modern large AI systems is hierarchical, often characterized by abrupt, qualitative shifts akin to phase transitions observed in physical systems. While these phenomena hold promise for uncovering the mechanisms behind neural networks and language models, existing theories remain fragmented, addressing specific cases. In this paper, we posit that parameter symmetry breaking and restoration serve as a unifying mechanism underlying these behaviors. We synthesize prior observations and show how this mechanism explains three distinct hierarchies in neural networks: learning dynamics, model complexity, and representation formation. By connecting these hierarchies, we highlight symmetry -- a cornerstone of theoretical physics -- as a potential fundamental principle in modern AI.

What if Eye...? Computationally Recreating Vision Evolution

Vision systems in nature show remarkable diversity, from simple light-sensitive patches to complex camera eyes with lenses. While natural selection has produced these eyes through countless mutations over millions of years, they represent just one set of realized evolutionary paths. Testing hypotheses about how environmental pressures shaped eye evolution remains challenging since we cannot experimentally isolate individual factors. Computational evolution offers a way to systematically explore alternative trajectories. Here we show how environmental demands drive three fundamental aspects of visual evolution through an artificial evolution framework that co-evolves both physical eye structure and neural processing in embodied agents. First, we demonstrate computational evidence that task specific selection drives bifurcation in eye evolution - orientation tasks like navigation in a maze leads to distributed compound-type eyes while an object discrimination task leads to the emergence of high-acuity camera-type eyes. Second, we reveal how optical innovations like lenses naturally emerge to resolve fundamental tradeoffs between light collection and spatial precision. Third, we uncover systematic scaling laws between visual acuity and neural processing, showing how task complexity drives coordinated evolution of sensory and computational capabilities. Our work introduces a novel paradigm that illuminates evolutionary principles shaping vision by creating targeted single-player games where embodied agents must simultaneously evolve visual systems and learn complex behaviors. Through our unified genetic encoding framework, these embodied agents serve as next-generation hypothesis testing machines while providing a foundation for designing manufacturable bio-inspired vision systems.

Self-Assembly of a Biologically Plausible Learning Circuit

Over the last four decades, the amazing success of deep learning has been driven by the use of Stochastic Gradient Descent (SGD) as the main optimization technique. The default implementation for the computation of the gradient for SGD is backpropagation, which, with its variations, is used to this day in almost all computer implementations. From the perspective of neuroscientists, however, the consensus is that backpropagation is unlikely to be used by the brain. Though several alternatives have been discussed, none is so far supported by experimental evidence. Here we propose a circuit for updating the weights in a network that is biologically plausible, works as well as backpropagation, and leads to verifiable predictions about the anatomy and the physiology of a characteristic motif of four plastic synapses between ascending and descending cortical streams. A key prediction of our proposal is a surprising property of self-assembly of the basic circuit, emerging from initial random connectivity and heterosynaptic plasticity rules.

On Generalization Bounds for Neural Networks with Low Rank Layers

While previous optimization results have suggested that deep neural networks tend to favour low-rank weight matrices, the implications of this inductive bias on generalization bounds remain underexplored. In this paper, we apply Maurer's chain rule for Gaussian complexity to analyze how low-rank layers in deep networks can prevent the accumulation of rank and dimensionality factors that typically multiply across layers. This approach yields generalization bounds for rank and spectral norm constrained networks. We compare our results to prior generalization bounds for deep networks, highlighting how deep networks with low-rank layers can achieve better generalization than those with full-rank layers. Additionally, we discuss how this framework provides new perspectives on the generalization capabilities of deep networks exhibiting neural collapse.