A universal compression theory: Lottery ticket hypothesis and superpolynomial scaling laws

When training large-scale models, the performance typically scales with the number of parameters and the dataset size according to a slow power law. A fundamental theoretical and practical question is whether comparable performance can be achieved with significantly smaller models and substantially less data. In this work, we provide a positive and constructive answer. We prove that a generic permutation-invariant function of $d$ objects can be asymptotically compressed into a function of $\operatorname{polylog} d$ objects with vanishing error. This theorem yields two key implications: (Ia) a large neural network can be compressed to polylogarithmic width while preserving its learning dynamics; (Ib) a large dataset can be compressed to polylogarithmic size while leaving the loss landscape of the corresponding model unchanged. (Ia) directly establishes a proof of the \textit{dynamical} lottery ticket hypothesis, which states that any ordinary network can be strongly compressed such that the learning dynamics and result remain unchanged. (Ib) shows that a neural scaling law of the form $L\sim d^{-\alpha}$ can be boosted to an arbitrarily fast power law decay, and ultimately to $\exp(-\alpha' \sqrt[m]{d})$.

Probing the Critical Point (CritPt) of AI Reasoning: a Frontier Physics Research Benchmark

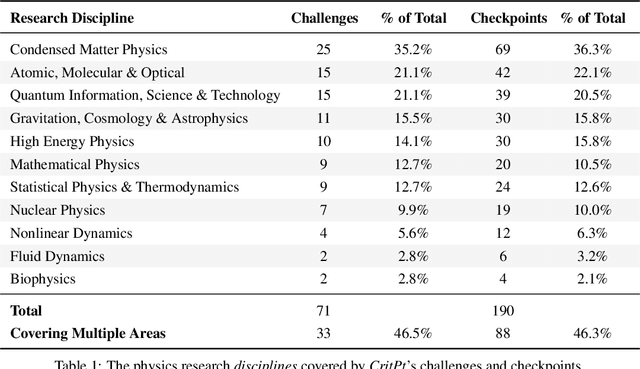
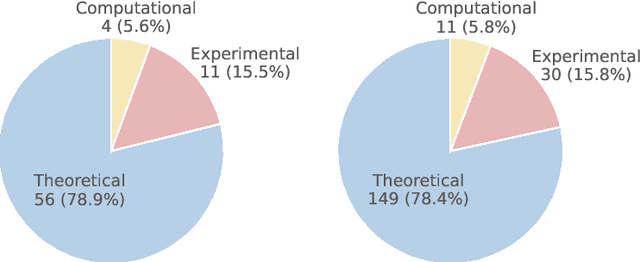
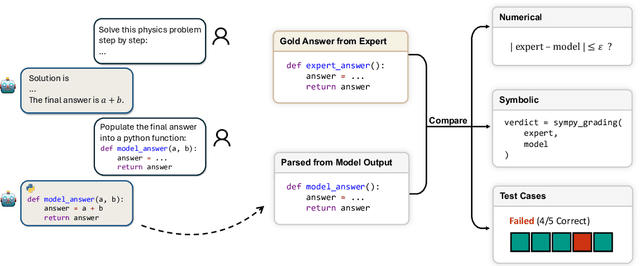
While large language models (LLMs) with reasoning capabilities are progressing rapidly on high-school math competitions and coding, can they reason effectively through complex, open-ended challenges found in frontier physics research? And crucially, what kinds of reasoning tasks do physicists want LLMs to assist with? To address these questions, we present the CritPt (Complex Research using Integrated Thinking - Physics Test, pronounced "critical point"), the first benchmark designed to test LLMs on unpublished, research-level reasoning tasks that broadly covers modern physics research areas, including condensed matter, quantum physics, atomic, molecular & optical physics, astrophysics, high energy physics, mathematical physics, statistical physics, nuclear physics, nonlinear dynamics, fluid dynamics and biophysics. CritPt consists of 71 composite research challenges designed to simulate full-scale research projects at the entry level, which are also decomposed to 190 simpler checkpoint tasks for more fine-grained insights. All problems are newly created by 50+ active physics researchers based on their own research. Every problem is hand-curated to admit a guess-resistant and machine-verifiable answer and is evaluated by an automated grading pipeline heavily customized for advanced physics-specific output formats. We find that while current state-of-the-art LLMs show early promise on isolated checkpoints, they remain far from being able to reliably solve full research-scale challenges: the best average accuracy among base models is only 4.0% , achieved by GPT-5 (high), moderately rising to around 10% when equipped with coding tools. Through the realistic yet standardized evaluation offered by CritPt, we highlight a large disconnect between current model capabilities and realistic physics research demands, offering a foundation to guide the development of scientifically grounded AI tools.

Hunyuan3D Studio: End-to-End AI Pipeline for Game-Ready 3D Asset Generation

The creation of high-quality 3D assets, a cornerstone of modern game development, has long been characterized by labor-intensive and specialized workflows. This paper presents Hunyuan3D Studio, an end-to-end AI-powered content creation platform designed to revolutionize the game production pipeline by automating and streamlining the generation of game-ready 3D assets. At its core, Hunyuan3D Studio integrates a suite of advanced neural modules (such as Part-level 3D Generation, Polygon Generation, Semantic UV, etc.) into a cohesive and user-friendly system. This unified framework allows for the rapid transformation of a single concept image or textual description into a fully-realized, production-quality 3D model complete with optimized geometry and high-fidelity PBR textures. We demonstrate that assets generated by Hunyuan3D Studio are not only visually compelling but also adhere to the stringent technical requirements of contemporary game engines, significantly reducing iteration time and lowering the barrier to entry for 3D content creation. By providing a seamless bridge from creative intent to technical asset, Hunyuan3D Studio represents a significant leap forward for AI-assisted workflows in game development and interactive media.

Hunyuan3D 2.1: From Images to High-Fidelity 3D Assets with Production-Ready PBR Material

3D AI-generated content (AIGC) is a passionate field that has significantly accelerated the creation of 3D models in gaming, film, and design. Despite the development of several groundbreaking models that have revolutionized 3D generation, the field remains largely accessible only to researchers, developers, and designers due to the complexities involved in collecting, processing, and training 3D models. To address these challenges, we introduce Hunyuan3D 2.1 as a case study in this tutorial. This tutorial offers a comprehensive, step-by-step guide on processing 3D data, training a 3D generative model, and evaluating its performance using Hunyuan3D 2.1, an advanced system for producing high-resolution, textured 3D assets. The system comprises two core components: the Hunyuan3D-DiT for shape generation and the Hunyuan3D-Paint for texture synthesis. We will explore the entire workflow, including data preparation, model architecture, training strategies, evaluation metrics, and deployment. By the conclusion of this tutorial, you will have the knowledge to finetune or develop a robust 3D generative model suitable for applications in gaming, virtual reality, and industrial design.

PhySense: Principle-Based Physics Reasoning Benchmarking for Large Language Models

Large language models (LLMs) have rapidly advanced and are increasingly capable of tackling complex scientific problems, including those in physics. Despite this progress, current LLMs often fail to emulate the concise, principle-based reasoning characteristic of human experts, instead generating lengthy and opaque solutions. This discrepancy highlights a crucial gap in their ability to apply core physical principles for efficient and interpretable problem solving. To systematically investigate this limitation, we introduce PhySense, a novel principle-based physics reasoning benchmark designed to be easily solvable by experts using guiding principles, yet deceptively difficult for LLMs without principle-first reasoning. Our evaluation across multiple state-of-the-art LLMs and prompt types reveals a consistent failure to align with expert-like reasoning paths, providing insights for developing AI systems with efficient, robust and interpretable principle-based scientific reasoning.

Provably Robust Training of Quantum Circuit Classifiers Against Parameter Noise

Advancements in quantum computing have spurred significant interest in harnessing its potential for speedups over classical systems. However, noise remains a major obstacle to achieving reliable quantum algorithms. In this work, we present a provably noise-resilient training theory and algorithm to enhance the robustness of parameterized quantum circuit classifiers. Our method, with a natural connection to Evolutionary Strategies, guarantees resilience to parameter noise with minimal adjustments to commonly used optimization algorithms. Our approach is function-agnostic and adaptable to various quantum circuits, successfully demonstrated in quantum phase classification tasks. By developing provably guaranteed optimization theory with quantum circuits, our work opens new avenues for practical, robust applications of near-term quantum computers.

Advancing AI-Scientist Understanding: Making LLM Think Like a Physicist with Interpretable Reasoning

Large Language Models (LLMs) are playing an expanding role in physics research by enhancing reasoning, symbolic manipulation, and numerical computation. However, ensuring the reliability and interpretability of their outputs remains a significant challenge. In our framework, we conceptualize the collaboration between AI and human scientists as a dynamic interplay among three modules: the reasoning module, the interpretation module, and the AI-scientist interaction module. Recognizing that effective physics reasoning demands rigorous logical consistency, quantitative precision, and deep integration with established theoretical models, we introduce the interpretation module to improve the understanding of AI-generated outputs, which is not previously explored in the literature. This module comprises multiple specialized agents, including summarizers, model builders, UI builders, and testers, which collaboratively structure LLM outputs within a physically grounded framework, by constructing a more interpretable science model. A case study demonstrates that our approach enhances transparency, facilitates validation, and strengthens AI-augmented reasoning in scientific discovery.

L$^2$M: Mutual Information Scaling Law for Long-Context Language Modeling

We rigorously establish a bipartite mutual information scaling law in natural language that governs long-range dependencies. This scaling law, which we show is distinct from and scales independently of the conventional two-point mutual information, is the key to understanding long-context language modeling. Using this scaling law, we formulate the Long-context Language Modeling (L$^2$M) condition, which relates a model's capacity for effective long context length modeling to the scaling of its latent state size for storing past information. Our results are validated through experiments on both transformers and state space models. This work establishes a theoretical foundation that guides the development of large language models toward longer context lengths.

TradingAgents: Multi-Agents LLM Financial Trading Framework

Significant progress has been made in automated problem-solving using societies of agents powered by large language models (LLMs). In finance, efforts have largely focused on single-agent systems handling specific tasks or multi-agent frameworks independently gathering data. However, multi-agent systems' potential to replicate real-world trading firms' collaborative dynamics remains underexplored. TradingAgents proposes a novel stock trading framework inspired by trading firms, featuring LLM-powered agents in specialized roles such as fundamental analysts, sentiment analysts, technical analysts, and traders with varied risk profiles. The framework includes Bull and Bear researcher agents assessing market conditions, a risk management team monitoring exposure, and traders synthesizing insights from debates and historical data to make informed decisions. By simulating a dynamic, collaborative trading environment, this framework aims to improve trading performance. Detailed architecture and extensive experiments reveal its superiority over baseline models, with notable improvements in cumulative returns, Sharpe ratio, and maximum drawdown, highlighting the potential of multi-agent LLM frameworks in financial trading.

SciCode: A Research Coding Benchmark Curated by Scientists

Since language models (LMs) now outperform average humans on many challenging tasks, it has become increasingly difficult to develop challenging, high-quality, and realistic evaluations. We address this issue by examining LMs' capabilities to generate code for solving real scientific research problems. Incorporating input from scientists and AI researchers in 16 diverse natural science sub-fields, including mathematics, physics, chemistry, biology, and materials science, we created a scientist-curated coding benchmark, SciCode. The problems in SciCode naturally factorize into multiple subproblems, each involving knowledge recall, reasoning, and code synthesis. In total, SciCode contains 338 subproblems decomposed from 80 challenging main problems. It offers optional descriptions specifying useful scientific background information and scientist-annotated gold-standard solutions and test cases for evaluation. Claude3.5-Sonnet, the best-performing model among those tested, can solve only 4.6% of the problems in the most realistic setting. We believe that SciCode demonstrates both contemporary LMs' progress towards becoming helpful scientific assistants and sheds light on the development and evaluation of scientific AI in the future.