OccamLLM: Fast and Exact Language Model Arithmetic in a Single Step

Despite significant advancements in text generation and reasoning, Large Language Models (LLMs) still face challenges in accurately performing complex arithmetic operations. To achieve accurate calculations, language model systems often enable LLMs to generate code for arithmetic operations. However, this approach compromises speed and security and, if finetuning is involved, risks the language model losing prior capabilities. We propose a framework that enables exact arithmetic in \textit{a single autoregressive step}, providing faster, more secure, and more interpretable LLM systems with arithmetic capabilities. We use the hidden states of an LLM to control a symbolic architecture which performs arithmetic. Our implementation using Llama 3 8B Instruct with OccamNet as a symbolic model (OccamLlama) achieves 100\% accuracy on single arithmetic operations ($+,-,\times,\div,\sin{},\cos{},\log{},\exp{},\sqrt{}$), outperforming GPT 4o and on par with GPT 4o using a code interpreter. OccamLlama also outperforms both Llama 3 8B Instruct and GPT 3.5 Turbo on multistep reasoning problems involving challenging arithmetic, thus enabling small LLMs to match the arithmetic performance of even much larger models. We will make our code public shortly.

QuanTA: Efficient High-Rank Fine-Tuning of LLMs with Quantum-Informed Tensor Adaptation

We propose Quantum-informed Tensor Adaptation (QuanTA), a novel, easy-to-implement, fine-tuning method with no inference overhead for large-scale pre-trained language models. By leveraging quantum-inspired methods derived from quantum circuit structures, QuanTA enables efficient high-rank fine-tuning, surpassing the limitations of Low-Rank Adaptation (LoRA)--low-rank approximation may fail for complicated downstream tasks. Our approach is theoretically supported by the universality theorem and the rank representation theorem to achieve efficient high-rank adaptations. Experiments demonstrate that QuanTA significantly enhances commonsense reasoning, arithmetic reasoning, and scalability compared to traditional methods. Furthermore, QuanTA shows superior performance with fewer trainable parameters compared to other approaches and can be designed to integrate with existing fine-tuning algorithms for further improvement, providing a scalable and efficient solution for fine-tuning large language models and advancing state-of-the-art in natural language processing.

Multimodal Learning for Crystalline Materials

Artificial intelligence (AI) has revolutionized the field of materials science by improving the prediction of properties and accelerating the discovery of novel materials. In recent years, publicly available material data repositories containing data for various material properties have grown rapidly. In this work, we introduce Multimodal Learning for Crystalline Materials (MLCM), a new method for training a foundation model for crystalline materials via multimodal alignment, where high-dimensional material properties (i.e. modalities) are connected in a shared latent space to produce highly useful material representations. We show the utility of MLCM on multiple axes: (i) MLCM achieves state-of-the-art performance for material property prediction on the challenging Materials Project database; (ii) MLCM enables a novel, highly accurate method for inverse design, allowing one to screen for stable material with desired properties; and (iii) MLCM allows the extraction of interpretable emergent features that may provide insight to material scientists. Further, we explore several novel methods for aligning an arbitrary number of modalities, improving upon prior art in multimodal learning that focuses on bimodal alignment. Our work brings innovations from the ongoing AI revolution into the domain of materials science and identifies materials as a testbed for the next generation of AI.

Constructive Assimilation: Boosting Contrastive Learning Performance through View Generation Strategies

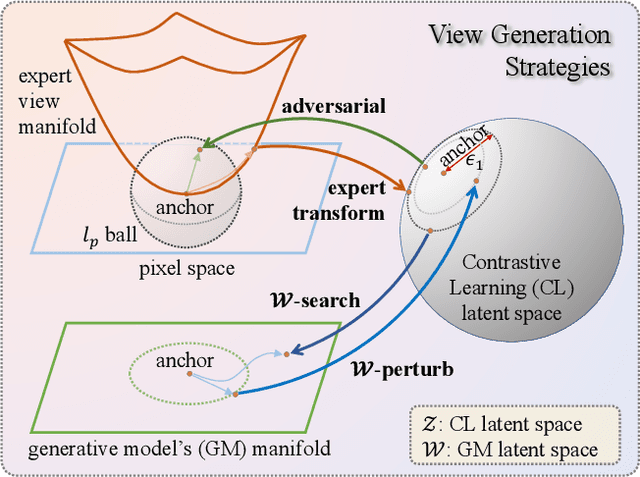
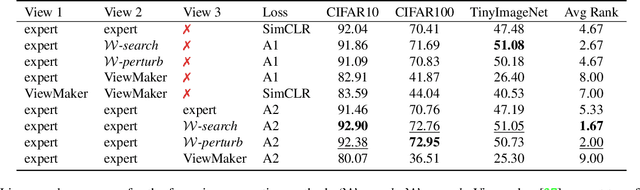
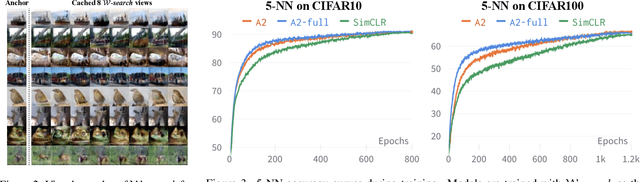
Transformations based on domain expertise (expert transformations), such as random-resized-crop and color-jitter, have proven critical to the success of contrastive learning techniques such as SimCLR. Recently, several attempts have been made to replace such domain-specific, human-designed transformations with generated views that are learned. However for imagery data, so far none of these view-generation methods has been able to outperform expert transformations. In this work, we tackle a different question: instead of replacing expert transformations with generated views, can we constructively assimilate generated views with expert transformations? We answer this question in the affirmative and propose a view generation method and a simple, effective assimilation method that together improve the state-of-the-art by up to ~3.6% on three different datasets. Importantly, we conduct a detailed empirical study that systematically analyzes a range of view generation and assimilation methods and provides a holistic picture of the efficacy of learned views in contrastive representation learning.

Model Stitching: Looking For Functional Similarity Between Representations

Model stitching (Lenc & Vedaldi 2015) is a compelling methodology to compare different neural network representations, because it allows us to measure to what degree they may be interchanged. We expand on a previous work from Bansal, Nakkiran & Barak which used model stitching to compare representations of the same shapes learned by differently seeded and/or trained neural networks of the same architecture. Our contribution enables us to compare the representations learned by layers with different shapes from neural networks with different architectures. We subsequently reveal unexpected behavior of model stitching. Namely, we find that stitching, based on convolutions, for small ResNets, can reach high accuracy if those layers come later in the first (sender) network than in the second (receiver), even if those layers are far apart.

Multi-Symmetry Ensembles: Improving Diversity and Generalization via Opposing Symmetries

Deep ensembles (DE) have been successful in improving model performance by learning diverse members via the stochasticity of random initialization. While recent works have attempted to promote further diversity in DE via hyperparameters or regularizing loss functions, these methods primarily still rely on a stochastic approach to explore the hypothesis space. In this work, we present Multi-Symmetry Ensembles (MSE), a framework for constructing diverse ensembles by capturing the multiplicity of hypotheses along symmetry axes, which explore the hypothesis space beyond stochastic perturbations of model weights and hyperparameters. We leverage recent advances in contrastive representation learning to create models that separately capture opposing hypotheses of invariant and equivariant symmetries and present a simple ensembling approach to efficiently combine appropriate hypotheses for a given task. We show that MSE effectively captures the multiplicity of conflicting hypotheses that is often required in large, diverse datasets like ImageNet. As a result of their inherent diversity, MSE improves classification performance, uncertainty quantification, and generalization across a series of transfer tasks.

Q-Flow: Generative Modeling for Differential Equations of Open Quantum Dynamics with Normalizing Flows

Studying the dynamics of open quantum systems holds the potential to enable breakthroughs both in fundamental physics and applications to quantum engineering and quantum computation. Due to the high-dimensional nature of the problem, customized deep generative neural networks have been instrumental in modeling the high-dimensional density matrix $\rho$, which is the key description for the dynamics of such systems. However, the complex-valued nature and normalization constraints of $\rho$, as well as its complicated dynamics, prohibit a seamless connection between open quantum systems and the recent advances in deep generative modeling. Here we lift that limitation by utilizing a reformulation of open quantum system dynamics to a partial differential equation (PDE) for a corresponding probability distribution $Q$, the Husimi Q function. Thus, we model the Q function seamlessly with off-the-shelf deep generative models such as normalizing flows. Additionally, we develop novel methods for learning normalizing flow evolution governed by high-dimensional PDEs, based on the Euler method and the application of the time-dependent variational principle. We name the resulting approach Q-Flow and demonstrate the scalability and efficiency of Q-Flow on open quantum system simulations, including the dissipative harmonic oscillator and the dissipative bosonic model. Q-Flow is superior to conventional PDE solvers and state-of-the-art physics-informed neural network solvers, especially in high-dimensional systems.

Koopman Operator learning for Accelerating Quantum Optimization and Machine Learning

Finding efficient optimization methods plays an important role for quantum optimization and quantum machine learning on near-term quantum computers. While backpropagation on classical computers is computationally efficient, obtaining gradients on quantum computers is not, because the computational complexity usually scales with the number of parameters and measurements. In this paper, we connect Koopman operator theory, which has been successful in predicting nonlinear dynamics, with natural gradient methods in quantum optimization. We propose a data-driven approach using Koopman operator learning to accelerate quantum optimization and quantum machine learning. We develop two new families of methods: the sliding window dynamic mode decomposition (DMD) and the neural DMD for efficiently updating parameters on quantum computers. We show that our methods can predict gradient dynamics on quantum computers and accelerate the variational quantum eigensolver used in quantum optimization, as well as quantum machine learning. We further implement our Koopman operator learning algorithm on a real IBM quantum computer and demonstrate their practical effectiveness.

On the Importance of Calibration in Semi-supervised Learning

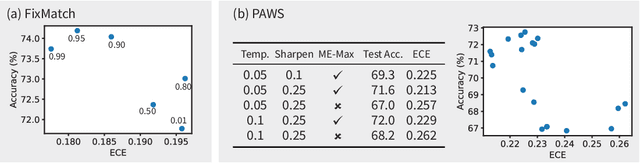
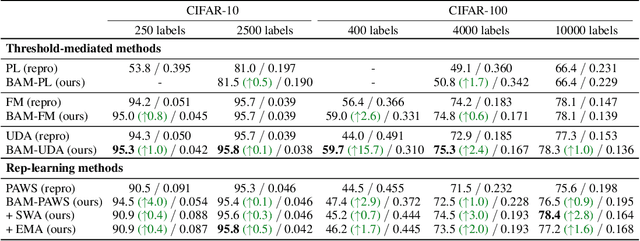
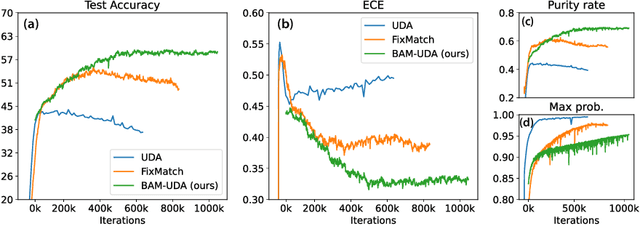
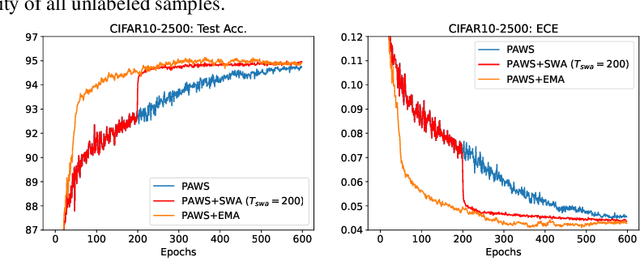
State-of-the-art (SOTA) semi-supervised learning (SSL) methods have been highly successful in leveraging a mix of labeled and unlabeled data by combining techniques of consistency regularization and pseudo-labeling. During pseudo-labeling, the model's predictions on unlabeled data are used for training and thus, model calibration is important in mitigating confirmation bias. Yet, many SOTA methods are optimized for model performance, with little focus directed to improve model calibration. In this work, we empirically demonstrate that model calibration is strongly correlated with model performance and propose to improve calibration via approximate Bayesian techniques. We introduce a family of new SSL models that optimizes for calibration and demonstrate their effectiveness across standard vision benchmarks of CIFAR-10, CIFAR-100 and ImageNet, giving up to 15.9% improvement in test accuracy. Furthermore, we also demonstrate their effectiveness in additional realistic and challenging problems, such as class-imbalanced datasets and in photonics science.

AI-Assisted Discovery of Quantitative and Formal Models in Social Science

In social science, formal and quantitative models, such as ones describing economic growth and collective action, are used to formulate mechanistic explanations, provide predictions, and uncover questions about observed phenomena. Here, we demonstrate the use of a machine learning system to aid the discovery of symbolic models that capture nonlinear and dynamical relationships in social science datasets. By extending neuro-symbolic methods to find compact functions and differential equations in noisy and longitudinal data, we show that our system can be used to discover interpretable models from real-world data in economics and sociology. Augmenting existing workflows with symbolic regression can help uncover novel relationships and explore counterfactual models during the scientific process. We propose that this AI-assisted framework can bridge parametric and non-parametric models commonly employed in social science research by systematically exploring the space of nonlinear models and enabling fine-grained control over expressivity and interpretability.