RURANET++: An Unsupervised Learning Method for Diabetic Macular Edema Based on SCSE Attention Mechanisms and Dynamic Multi-Projection Head Clustering

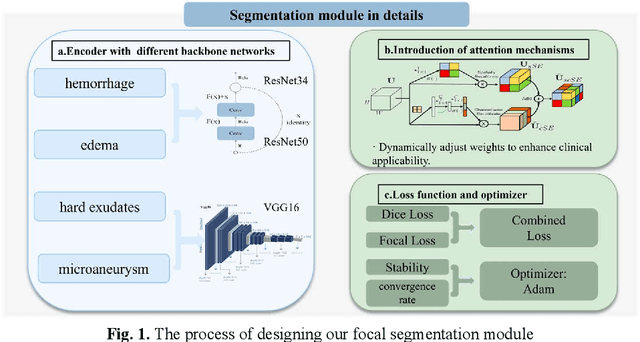
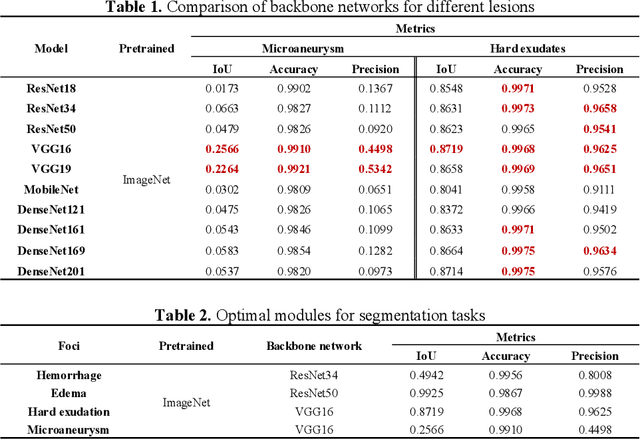
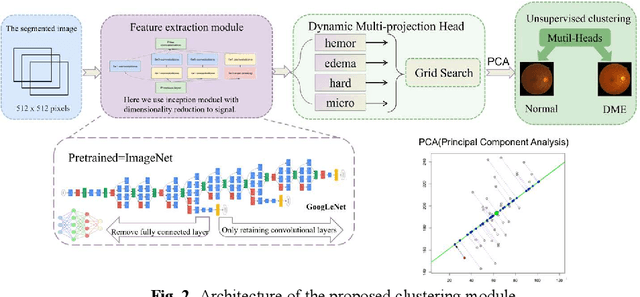
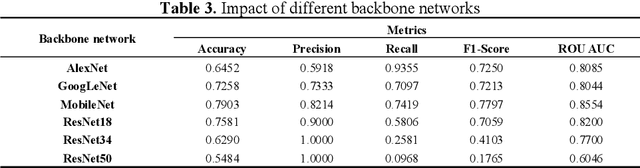
Diabetic Macular Edema (DME), a prevalent complication among diabetic patients, constitutes a major cause of visual impairment and blindness. Although deep learning has achieved remarkable progress in medical image analysis, traditional DME diagnosis still relies on extensive annotated data and subjective ophthalmologist assessments, limiting practical applications. To address this, we present RURANET++, an unsupervised learning-based automated DME diagnostic system. This framework incorporates an optimized U-Net architecture with embedded Spatial and Channel Squeeze & Excitation (SCSE) attention mechanisms to enhance lesion feature extraction. During feature processing, a pre-trained GoogLeNet model extracts deep features from retinal images, followed by PCA-based dimensionality reduction to 50 dimensions for computational efficiency. Notably, we introduce a novel clustering algorithm employing multi-projection heads to explicitly control cluster diversity while dynamically adjusting similarity thresholds, thereby optimizing intra-class consistency and inter-class discrimination. Experimental results demonstrate superior performance across multiple metrics, achieving maximum accuracy (0.8411), precision (0.8593), recall (0.8411), and F1-score (0.8390), with exceptional clustering quality. This work provides an efficient unsupervised solution for DME diagnosis with significant clinical implications.

TARGA: Targeted Synthetic Data Generation for Practical Reasoning over Structured Data

Semantic parsing, which converts natural language questions into logic forms, plays a crucial role in reasoning within structured environments. However, existing methods encounter two significant challenges: reliance on extensive manually annotated datasets and limited generalization capability to unseen examples. To tackle these issues, we propose Targeted Synthetic Data Generation (TARGA), a practical framework that dynamically generates high-relevance synthetic data without manual annotation. Starting from the pertinent entities and relations of a given question, we probe for the potential relevant queries through layer-wise expansion and cross-layer combination. Then we generate corresponding natural language questions for these constructed queries to jointly serve as the synthetic demonstrations for in-context learning. Experiments on multiple knowledge base question answering (KBQA) datasets demonstrate that TARGA, using only a 7B-parameter model, substantially outperforms existing non-fine-tuned methods that utilize close-sourced model, achieving notable improvements in F1 scores on GrailQA(+7.7) and KBQA-Agent(+12.2). Furthermore, TARGA also exhibits superior sample efficiency, robustness, and generalization capabilities under non-I.I.D. settings.

QueryAgent: A Reliable and Efficient Reasoning Framework with Environmental Feedback based Self-Correction

Employing Large Language Models (LLMs) for semantic parsing has achieved remarkable success. However, we find existing methods fall short in terms of reliability and efficiency when hallucinations are encountered. In this paper, we address these challenges with a framework called QueryAgent, which solves a question step-by-step and performs step-wise self-correction. We introduce an environmental feedback-based self-correction method called ERASER. Unlike traditional approaches, ERASER leverages rich environmental feedback in the intermediate steps to perform selective and differentiated self-correction only when necessary. Experimental results demonstrate that QueryAgent notably outperforms all previous few-shot methods using only one example on GrailQA and GraphQ by 7.0 and 15.0 F1. Moreover, our approach exhibits superiority in terms of efficiency, including runtime, query overhead, and API invocation costs. By leveraging ERASER, we further improve another baseline (i.e., AgentBench) by approximately 10 points, revealing the strong transferability of our approach.

Koopman Operator learning for Accelerating Quantum Optimization and Machine Learning

Finding efficient optimization methods plays an important role for quantum optimization and quantum machine learning on near-term quantum computers. While backpropagation on classical computers is computationally efficient, obtaining gradients on quantum computers is not, because the computational complexity usually scales with the number of parameters and measurements. In this paper, we connect Koopman operator theory, which has been successful in predicting nonlinear dynamics, with natural gradient methods in quantum optimization. We propose a data-driven approach using Koopman operator learning to accelerate quantum optimization and quantum machine learning. We develop two new families of methods: the sliding window dynamic mode decomposition (DMD) and the neural DMD for efficiently updating parameters on quantum computers. We show that our methods can predict gradient dynamics on quantum computers and accelerate the variational quantum eigensolver used in quantum optimization, as well as quantum machine learning. We further implement our Koopman operator learning algorithm on a real IBM quantum computer and demonstrate their practical effectiveness.