A Cosmic-Scale Benchmark for Symmetry-Preserving Data Processing

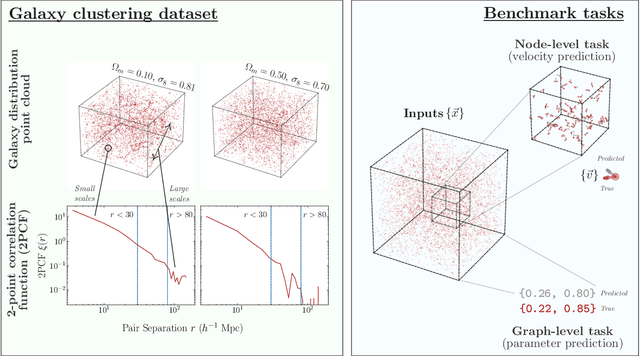
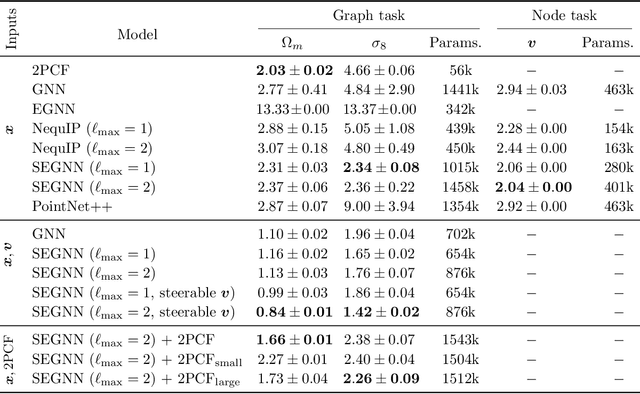
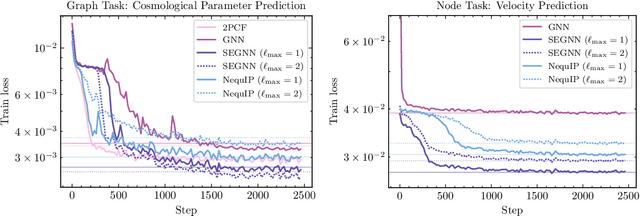
Efficiently processing structured point cloud data while preserving multiscale information is a key challenge across domains, from graphics to atomistic modeling. Using a curated dataset of simulated galaxy positions and properties, represented as point clouds, we benchmark the ability of graph neural networks to simultaneously capture local clustering environments and long-range correlations. Given the homogeneous and isotropic nature of the Universe, the data exhibits a high degree of symmetry. We therefore focus on evaluating the performance of Euclidean symmetry-preserving ($E(3)$-equivariant) graph neural networks, showing that they can outperform non-equivariant counterparts and domain-specific information extraction techniques in downstream performance as well as simulation-efficiency. However, we find that current architectures fail to capture information from long-range correlations as effectively as domain-specific baselines, motivating future work on architectures better suited for extracting long-range information.

CodonMPNN for Organism Specific and Codon Optimal Inverse Folding

Generating protein sequences conditioned on protein structures is an impactful technique for protein engineering. When synthesizing engineered proteins, they are commonly translated into DNA and expressed in an organism such as yeast. One difficulty in this process is that the expression rates can be low due to suboptimal codon sequences for expressing a protein in a host organism. We propose CodonMPNN, which generates a codon sequence conditioned on a protein backbone structure and an organism label. If naturally occurring DNA sequences are close to codon optimality, CodonMPNN could learn to generate codon sequences with higher expression yields than heuristic codon choices for generated amino acid sequences. Experiments show that CodonMPNN retains the performance of previous inverse folding approaches and recovers wild-type codons more frequently than baselines. Furthermore, CodonMPNN has a higher likelihood of generating high-fitness codon sequences than low-fitness codon sequences for the same protein sequence. Code is available at https://github.com/HannesStark/CodonMPNN.

Over-Squashing in Riemannian Graph Neural Networks

Most graph neural networks (GNNs) are prone to the phenomenon of over-squashing in which node features become insensitive to information from distant nodes in the graph. Recent works have shown that the topology of the graph has the greatest impact on over-squashing, suggesting graph rewiring approaches as a suitable solution. In this work, we explore whether over-squashing can be mitigated through the embedding space of the GNN. In particular, we consider the generalization of Hyperbolic GNNs (HGNNs) to Riemannian manifolds of variable curvature in which the geometry of the embedding space is faithful to the graph's topology. We derive bounds on the sensitivity of the node features in these Riemannian GNNs as the number of layers increases, which yield promising theoretical and empirical results for alleviating over-squashing in graphs with negative curvature.

AI-Assisted Discovery of Quantitative and Formal Models in Social Science

In social science, formal and quantitative models, such as ones describing economic growth and collective action, are used to formulate mechanistic explanations, provide predictions, and uncover questions about observed phenomena. Here, we demonstrate the use of a machine learning system to aid the discovery of symbolic models that capture nonlinear and dynamical relationships in social science datasets. By extending neuro-symbolic methods to find compact functions and differential equations in noisy and longitudinal data, we show that our system can be used to discover interpretable models from real-world data in economics and sociology. Augmenting existing workflows with symbolic regression can help uncover novel relationships and explore counterfactual models during the scientific process. We propose that this AI-assisted framework can bridge parametric and non-parametric models commonly employed in social science research by systematically exploring the space of nonlinear models and enabling fine-grained control over expressivity and interpretability.

Differentially Private Supervised Manifold Learning with Applications like Private Image Retrieval

Differential Privacy offers strong guarantees such as immutable privacy under post processing. Thus it is often looked to as a solution to learning on scattered and isolated data. This work focuses on supervised manifold learning, a paradigm that can generate fine-tuned manifolds for a target use case. Our contributions are two fold. 1) We present a novel differentially private method \textit{PrivateMail} for supervised manifold learning, the first of its kind to our knowledge. 2) We provide a novel private geometric embedding scheme for our experimental use case. We experiment on private "content based image retrieval" - embedding and querying the nearest neighbors of images in a private manner - and show extensive privacy-utility tradeoff results, as well as the computational efficiency and practicality of our methods.

Splintering with distributions: A stochastic decoy scheme for private computation

Performing computations while maintaining privacy is an important problem in todays distributed machine learning solutions. Consider the following two set ups between a client and a server, where in setup i) the client has a public data vector $\mathbf{x}$, the server has a large private database of data vectors $\mathcal{B}$ and the client wants to find the inner products $\langle \mathbf{x,y_k} \rangle, \forall \mathbf{y_k} \in \mathcal{B}$. The client does not want the server to learn $\mathbf{x}$ while the server does not want the client to learn the records in its database. This is in contrast to another setup ii) where the client would like to perform an operation solely on its data, such as computation of a matrix inverse on its data matrix $\mathbf{M}$, but would like to use the superior computing ability of the server to do so without having to leak $\mathbf{M}$ to the server. \par We present a stochastic scheme for splitting the client data into privatized shares that are transmitted to the server in such settings. The server performs the requested operations on these shares instead of on the raw client data at the server. The obtained intermediate results are sent back to the client where they are assembled by the client to obtain the final result.