On the necessity of adaptive regularisation:Optimal anytime online learning on $\boldsymbol{\ell_p}$-balls

We study online convex optimization on $\ell_p$-balls in $\mathbb{R}^d$ for $p > 2$. While always sub-linear, the optimal regret exhibits a shift between the high-dimensional setting ($d > T$), when the dimension $d$ is greater than the time horizon $T$ and the low-dimensional setting ($d \leq T$). We show that Follow-the-Regularised-Leader (FTRL) with time-varying regularisation which is adaptive to the dimension regime is anytime optimal for all dimension regimes. Motivated by this, we ask whether it is possible to obtain anytime optimality of FTRL with fixed non-adaptive regularisation. Our main result establishes that for separable regularisers, adaptivity in the regulariser is necessary, and that any fixed regulariser will be sub-optimal in one of the two dimension regimes. Finally, we provide lower bounds which rule out sub-linear regret bounds for the linear bandit problem in sufficiently high-dimension for all $\ell_p$-balls with $p \geq 1$.

Early-Stopped Mirror Descent for Linear Regression over Convex Bodies

Early-stopped iterative optimization methods are widely used as alternatives to explicit regularization, and direct comparisons between early-stopping and explicit regularization have been established for many optimization geometries. However, most analyses depend heavily on the specific properties of the optimization geometry or strong convexity of the empirical objective, and it remains unclear whether early-stopping could ever be less statistically efficient than explicit regularization for some particular shape constraint, especially in the overparameterized regime. To address this question, we study the setting of high-dimensional linear regression under additive Gaussian noise when the ground truth is assumed to lie in a known convex body and the task is to minimize the in-sample mean squared error. Our main result shows that for any convex body and any design matrix, up to an absolute constant factor, the worst-case risk of unconstrained early-stopped mirror descent with an appropriate potential is at most that of the least squares estimator constrained to the convex body. We achieve this by constructing algorithmic regularizers based on the Minkowski functional of the convex body.

Black-Box Uniform Stability for Non-Euclidean Empirical Risk Minimization

We study first-order algorithms that are uniformly stable for empirical risk minimization (ERM) problems that are convex and smooth with respect to $p$-norms, $p \geq 1$. We propose a black-box reduction method that, by employing properties of uniformly convex regularizers, turns an optimization algorithm for H\"older smooth convex losses into a uniformly stable learning algorithm with optimal statistical risk bounds on the excess risk, up to a constant factor depending on $p$. Achieving a black-box reduction for uniform stability was posed as an open question by (Attia and Koren, 2022), which had solved the Euclidean case $p=2$. We explore applications that leverage non-Euclidean geometry in addressing binary classification problems.

Learning Loss Landscapes in Preference Optimization

We present an empirical study investigating how specific properties of preference datasets, such as mixed-quality or noisy data, affect the performance of Preference Optimization (PO) algorithms. Our experiments, conducted in MuJoCo environments, reveal several scenarios where state-of-the-art PO methods experience significant drops in performance. To address this issue, we introduce a novel PO framework based on mirror descent, which can recover existing methods like Direct Preference Optimization (DPO) and Odds-Ratio Preference Optimization (ORPO) for specific choices of the mirror map. Within this framework, we employ evolutionary strategies to discover new loss functions capable of handling the identified problematic scenarios. These new loss functions lead to significant performance improvements over DPO and ORPO across several tasks. Additionally, we demonstrate the generalization capability of our approach by applying the discovered loss functions to fine-tuning large language models using mixed-quality data, where they outperform ORPO.

Robust Gradient Descent for Phase Retrieval

Recent progress in robust statistical learning has mainly tackled convex problems, like mean estimation or linear regression, with non-convex challenges receiving less attention. Phase retrieval exemplifies such a non-convex problem, requiring the recovery of a signal from only the magnitudes of its linear measurements, without phase (sign) information. While several non-convex methods, especially those involving the Wirtinger Flow algorithm, have been proposed for noiseless or mild noise settings, developing solutions for heavy-tailed noise and adversarial corruption remains an open challenge. In this paper, we investigate an approach that leverages robust gradient descent techniques to improve the Wirtinger Flow algorithm's ability to simultaneously cope with fourth moment bounded noise and adversarial contamination in both the inputs (covariates) and outputs (responses). We address two scenarios: known zero-mean noise and completely unknown noise. For the latter, we propose a preprocessing step that alters the problem into a new format that does not fit traditional phase retrieval approaches but can still be resolved with a tailored version of the algorithm for the zero-mean noise context.

Differentiable Cost-Parameterized Monge Map Estimators

Within the field of optimal transport (OT), the choice of ground cost is crucial to ensuring that the optimality of a transport map corresponds to usefulness in real-world applications. It is therefore desirable to use known information to tailor cost functions and hence learn OT maps which are adapted to the problem at hand. By considering a class of neural ground costs whose Monge maps have a known form, we construct a differentiable Monge map estimator which can be optimized to be consistent with known information about an OT map. In doing so, we simultaneously learn both an OT map estimator and a corresponding adapted cost function. Through suitable choices of loss function, our method provides a general approach for incorporating prior information about the Monge map itself when learning adapted OT maps and cost functions.

Meta-learning the mirror map in policy mirror descent

Policy Mirror Descent (PMD) is a popular framework in reinforcement learning, serving as a unifying perspective that encompasses numerous algorithms. These algorithms are derived through the selection of a mirror map and enjoy finite-time convergence guarantees. Despite its popularity, the exploration of PMD's full potential is limited, with the majority of research focusing on a particular mirror map -- namely, the negative entropy -- which gives rise to the renowned Natural Policy Gradient (NPG) method. It remains uncertain from existing theoretical studies whether the choice of mirror map significantly influences PMD's efficacy. In our work, we conduct empirical investigations to show that the conventional mirror map choice (NPG) often yields less-than-optimal outcomes across several standard benchmark environments. By applying a meta-learning approach, we identify more efficient mirror maps that enhance performance, both on average and in terms of best performance achieved along the training trajectory. We analyze the characteristics of these learned mirror maps and reveal shared traits among certain settings. Our results suggest that mirror maps have the potential to be adaptable across various environments, raising questions about how to best match a mirror map to an environment's structure and characteristics.

Generalization Bounds for Label Noise Stochastic Gradient Descent

We develop generalization error bounds for stochastic gradient descent (SGD) with label noise in non-convex settings under uniform dissipativity and smoothness conditions. Under a suitable choice of semimetric, we establish a contraction in Wasserstein distance of the label noise stochastic gradient flow that depends polynomially on the parameter dimension $d$. Using the framework of algorithmic stability, we derive time-independent generalisation error bounds for the discretized algorithm with a constant learning rate. The error bound we achieve scales polynomially with $d$ and with the rate of $n^{-2/3}$, where $n$ is the sample size. This rate is better than the best-known rate of $n^{-1/2}$ established for stochastic gradient Langevin dynamics (SGLD) -- which employs parameter-independent Gaussian noise -- under similar conditions. Our analysis offers quantitative insights into the effect of label noise.

Sample-Efficiency in Multi-Batch Reinforcement Learning: The Need for Dimension-Dependent Adaptivity

We theoretically explore the relationship between sample-efficiency and adaptivity in reinforcement learning. An algorithm is sample-efficient if it uses a number of queries $n$ to the environment that is polynomial in the dimension $d$ of the problem. Adaptivity refers to the frequency at which queries are sent and feedback is processed to update the querying strategy. To investigate this interplay, we employ a learning framework that allows sending queries in $K$ batches, with feedback being processed and queries updated after each batch. This model encompasses the whole adaptivity spectrum, ranging from non-adaptive 'offline' ($K=1$) to fully adaptive ($K=n$) scenarios, and regimes in between. For the problems of policy evaluation and best-policy identification under $d$-dimensional linear function approximation, we establish $\Omega(\log \log d)$ lower bounds on the number of batches $K$ required for sample-efficient algorithms with $n = O(poly(d))$ queries. Our results show that just having adaptivity ($K>1$) does not necessarily guarantee sample-efficiency. Notably, the adaptivity-boundary for sample-efficiency is not between offline reinforcement learning ($K=1$), where sample-efficiency was known to not be possible, and adaptive settings. Instead, the boundary lies between different regimes of adaptivity and depends on the problem dimension.

Optimal Convergence Rate for Exact Policy Mirror Descent in Discounted Markov Decision Processes

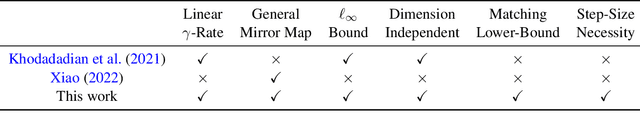
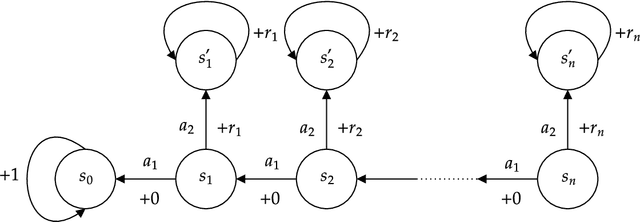
The classical algorithms used in tabular reinforcement learning (Value Iteration and Policy Iteration) have been shown to converge linearly with a rate given by the discount factor $\gamma$ of a discounted Markov Decision Process. Recently, there has been an increased interest in the study of gradient based methods. In this work, we show that the dimension-free linear $\gamma$-rate of classical reinforcement learning algorithms can be achieved by a general family of unregularised Policy Mirror Descent (PMD) algorithms under an adaptive step-size. We also provide a matching worst-case lower-bound that demonstrates that the $\gamma$-rate is optimal for PMD methods. Our work offers a novel perspective on the convergence of PMD. We avoid the use of the performance difference lemma beyond establishing the monotonic improvement of the iterates, which leads to a simple analysis that may be of independent interest. We also extend our analysis to the inexact setting and establish the first dimension-free $\varepsilon$-optimal sample complexity for unregularised PMD under a generative model, improving upon the best-known result.