On the necessity of adaptive regularisation:Optimal anytime online learning on $\boldsymbol{\ell_p}$-balls

We study online convex optimization on $\ell_p$-balls in $\mathbb{R}^d$ for $p > 2$. While always sub-linear, the optimal regret exhibits a shift between the high-dimensional setting ($d > T$), when the dimension $d$ is greater than the time horizon $T$ and the low-dimensional setting ($d \leq T$). We show that Follow-the-Regularised-Leader (FTRL) with time-varying regularisation which is adaptive to the dimension regime is anytime optimal for all dimension regimes. Motivated by this, we ask whether it is possible to obtain anytime optimality of FTRL with fixed non-adaptive regularisation. Our main result establishes that for separable regularisers, adaptivity in the regulariser is necessary, and that any fixed regulariser will be sub-optimal in one of the two dimension regimes. Finally, we provide lower bounds which rule out sub-linear regret bounds for the linear bandit problem in sufficiently high-dimension for all $\ell_p$-balls with $p \geq 1$.

Sample-Efficiency in Multi-Batch Reinforcement Learning: The Need for Dimension-Dependent Adaptivity

We theoretically explore the relationship between sample-efficiency and adaptivity in reinforcement learning. An algorithm is sample-efficient if it uses a number of queries $n$ to the environment that is polynomial in the dimension $d$ of the problem. Adaptivity refers to the frequency at which queries are sent and feedback is processed to update the querying strategy. To investigate this interplay, we employ a learning framework that allows sending queries in $K$ batches, with feedback being processed and queries updated after each batch. This model encompasses the whole adaptivity spectrum, ranging from non-adaptive 'offline' ($K=1$) to fully adaptive ($K=n$) scenarios, and regimes in between. For the problems of policy evaluation and best-policy identification under $d$-dimensional linear function approximation, we establish $\Omega(\log \log d)$ lower bounds on the number of batches $K$ required for sample-efficient algorithms with $n = O(poly(d))$ queries. Our results show that just having adaptivity ($K>1$) does not necessarily guarantee sample-efficiency. Notably, the adaptivity-boundary for sample-efficiency is not between offline reinforcement learning ($K=1$), where sample-efficiency was known to not be possible, and adaptive settings. Instead, the boundary lies between different regimes of adaptivity and depends on the problem dimension.

Optimal Convergence Rate for Exact Policy Mirror Descent in Discounted Markov Decision Processes

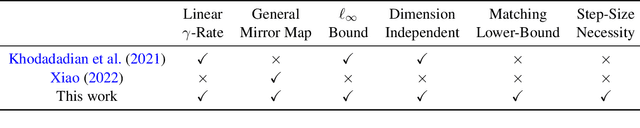
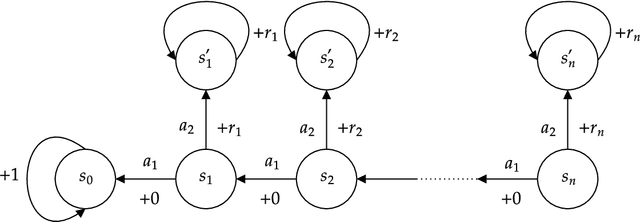
The classical algorithms used in tabular reinforcement learning (Value Iteration and Policy Iteration) have been shown to converge linearly with a rate given by the discount factor $\gamma$ of a discounted Markov Decision Process. Recently, there has been an increased interest in the study of gradient based methods. In this work, we show that the dimension-free linear $\gamma$-rate of classical reinforcement learning algorithms can be achieved by a general family of unregularised Policy Mirror Descent (PMD) algorithms under an adaptive step-size. We also provide a matching worst-case lower-bound that demonstrates that the $\gamma$-rate is optimal for PMD methods. Our work offers a novel perspective on the convergence of PMD. We avoid the use of the performance difference lemma beyond establishing the monotonic improvement of the iterates, which leads to a simple analysis that may be of independent interest. We also extend our analysis to the inexact setting and establish the first dimension-free $\varepsilon$-optimal sample complexity for unregularised PMD under a generative model, improving upon the best-known result.