Optimal Convergence Rate for Exact Policy Mirror Descent in Discounted Markov Decision Processes
Paper and Code
Feb 22, 2023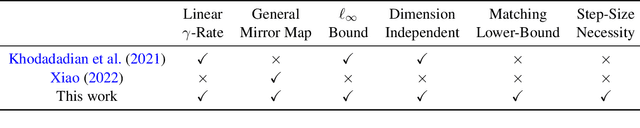
The classical algorithms used in tabular reinforcement learning (Value Iteration and Policy Iteration) have been shown to converge linearly with a rate given by the discount factor $\gamma$ of a discounted Markov Decision Process. Recently, there has been an increased interest in the study of gradient based methods. In this work, we show that the dimension-free linear $\gamma$-rate of classical reinforcement learning algorithms can be achieved by a general family of unregularised Policy Mirror Descent (PMD) algorithms under an adaptive step-size. We also provide a matching worst-case lower-bound that demonstrates that the $\gamma$-rate is optimal for PMD methods. Our work offers a novel perspective on the convergence of PMD. We avoid the use of the performance difference lemma beyond establishing the monotonic improvement of the iterates, which leads to a simple analysis that may be of independent interest. We also extend our analysis to the inexact setting and establish the first dimension-free $\varepsilon$-optimal sample complexity for unregularised PMD under a generative model, improving upon the best-known result.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge