Aggregation with Exponential Weights is Optimal in Expectation

The aggregation with exponential weights (AEW) estimator is not fully understood in the basic setting of model selection aggregation with squared loss. In particular, whether it is minimax-rate optimal in expectation for large enough fixed temperatures and under random design has been an open problem since its introduction, which was explicitly posed by Lecué and Mendelson (2013). In this paper, we settle this problem by showing that \emph{without} requiring a Bernstein-type assumption, the AEW indeed achieves the excess risk $T \log (M) / (n+1)$ in expectation, whenever the temperature $T$ satisfies $(L^2/T)\exp(B/T)\leq μ/2$. Here, the number of dictionary elements is $M$, the estimator has observed $n$ i.i.d. samples from any distribution, and the loss is assumed to be bounded by $B$, $L$-Lipschitz continuous and $μ$-strongly convex. For squared loss, we show that $T\geq 4 b^2$ suffices when the predictions and labels are $[0,b]$-valued. Because AEW is known to be suboptimal in expectation for temperatures below some constant, this shows that AEW has a sharp phase transition when the temperature is large enough but constant, as conjectured by Lecué and Mendelson.

Cutting LLM Evaluation Costs with SySRs: A Bandit Algorithm that Provably Exploits Model Similarity

Large Language Models are typically benchmarked by evaluating every model on every test query. For practitioners seeking the best model to deploy, this is often wasteful: if a model clearly performs worse than others, there is no need to precisely estimate its performance. Best-arm identification algorithms can be naturally applied to drastically reduce costs by adaptively allocating evaluation budget. Further, language models often respond similarly to the same prompt-a property previous work has tried to leverage with mixed success. We propose Synchronized Successive Rejects (SySRs), augmenting the classical Successive Rejects algorithm with paired comparisons. Unlike prior attempts to leverage model similarity in best-model identification, our approach is hyperparameter-free and enjoys performance guarantees that improve with the degree of similarity between evaluated models. Empirically, our method outperforms all baselines in terms of average error rate across 15 standard benchmarks, and in terms of worst-case budget for reliably identifying the best model.

Hedging on the Frontier: Learning New Tasks with Few Samples

When a learner faces a new task with few samples, it must leverage any available side information. In practice, this often comes in the form of model evaluations on related tasks in public benchmarks. A key question then is how to model task relatedness such that it is both realistic and the benchmark evaluations lead to provable gains. Empirically, we observe that weak monotonicity is often approximately satisfied: if a model dominates another on many benchmarks, it also tends to outperform on the new task. We explore the statistical complexity of learning under (approximate) weak monotonicity, leveraging it within two learning paradigms: transfer learning and model selection aggregation. We show that not only can we prune the model class based on monotonicity, but we can also further adapt to the geometry of the available trade-offs by hedging on the frontier.

On the sample complexity of semi-supervised multi-objective learning

In multi-objective learning (MOL), several possibly competing prediction tasks must be solved jointly by a single model. Achieving good trade-offs may require a model class $\mathcal{G}$ with larger capacity than what is necessary for solving the individual tasks. This, in turn, increases the statistical cost, as reflected in known MOL bounds that depend on the complexity of $\mathcal{G}$. We show that this cost is unavoidable for some losses, even in an idealized semi-supervised setting, where the learner has access to the Bayes-optimal solutions for the individual tasks as well as the marginal distributions over the covariates. On the other hand, for objectives defined with Bregman losses, we prove that the complexity of $\mathcal{G}$ may come into play only in terms of unlabeled data. Concretely, we establish sample complexity upper bounds, showing precisely when and how unlabeled data can significantly alleviate the need for labeled data. These rates are achieved by a simple, semi-supervised algorithm via pseudo-labeling.

Learning Pareto manifolds in high dimensions: How can regularization help?

Simultaneously addressing multiple objectives is becoming increasingly important in modern machine learning. At the same time, data is often high-dimensional and costly to label. For a single objective such as prediction risk, conventional regularization techniques are known to improve generalization when the data exhibits low-dimensional structure like sparsity. However, it is largely unexplored how to leverage this structure in the context of multi-objective learning (MOL) with multiple competing objectives. In this work, we discuss how the application of vanilla regularization approaches can fail, and propose a two-stage MOL framework that can successfully leverage low-dimensional structure. We demonstrate its effectiveness experimentally for multi-distribution learning and fairness-risk trade-offs.

Early-Stopped Mirror Descent for Linear Regression over Convex Bodies

Early-stopped iterative optimization methods are widely used as alternatives to explicit regularization, and direct comparisons between early-stopping and explicit regularization have been established for many optimization geometries. However, most analyses depend heavily on the specific properties of the optimization geometry or strong convexity of the empirical objective, and it remains unclear whether early-stopping could ever be less statistically efficient than explicit regularization for some particular shape constraint, especially in the overparameterized regime. To address this question, we study the setting of high-dimensional linear regression under additive Gaussian noise when the ground truth is assumed to lie in a known convex body and the task is to minimize the in-sample mean squared error. Our main result shows that for any convex body and any design matrix, up to an absolute constant factor, the worst-case risk of unconstrained early-stopped mirror descent with an appropriate potential is at most that of the least squares estimator constrained to the convex body. We achieve this by constructing algorithmic regularizers based on the Minkowski functional of the convex body.

A Framework for Verification of Wasserstein Adversarial Robustness

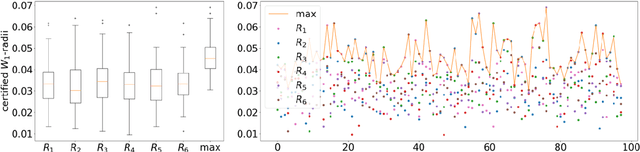
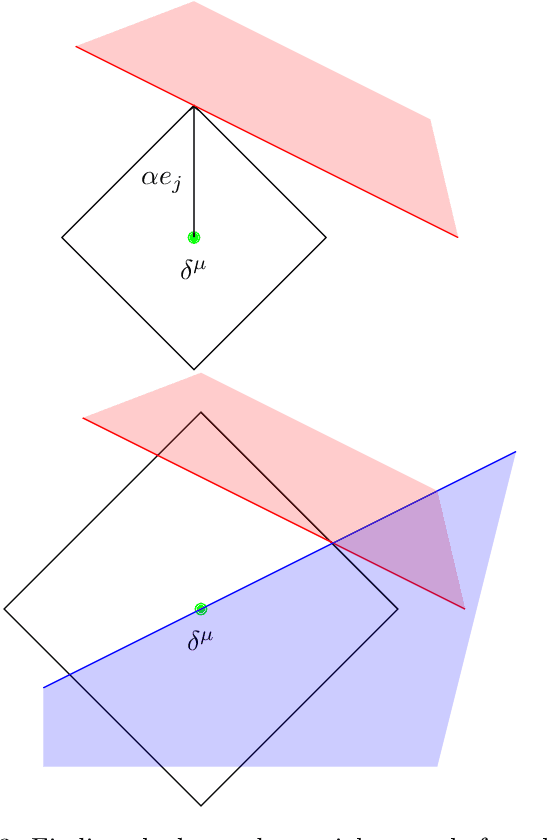
Machine learning image classifiers are susceptible to adversarial and corruption perturbations. Adding imperceptible noise to images can lead to severe misclassifications of the machine learning model. Using $L_p$-norms for measuring the size of the noise fails to capture human similarity perception, which is why optimal transport based distance measures like the Wasserstein metric are increasingly being used in the field of adversarial robustness. Verifying the robustness of classifiers using the Wasserstein metric can be achieved by proving the absence of adversarial examples (certification) or proving their presence (attack). In this work we present a framework based on the work by Levine and Feizi, which allows us to transfer existing certification methods for convex polytopes or $L_1$-balls to the Wasserstein threat model. The resulting certification can be complete or incomplete, depending on whether convex polytopes or $L_1$-balls were chosen. Additionally, we present a new Wasserstein adversarial attack that is projected gradient descent based and which has a significantly reduced computational burden compared to existing attack approaches.