Support Tokens, Stability Margins, and a New Foundation for Robust LLMs

Self-attention is usually described as a flexible, content-adaptive way to mix a token with information from its past. We re-interpret causal self-attention transformers, the backbone of modern foundation models, within a probabilistic framework, much like how classical PCA is extended to probabilistic PCA. However, this re-formulation reveals a surprising and deeper structural insight: due to a change-of-variables phenomenon, a barrier constraint emerges on the self-attention parameters. This induces a highly structured geometry on the token space, providing theoretical insights into the dynamics of LLM decoding. This reveals a boundary where attention becomes ill-conditioned, leading to a margin interpretation similar to classical support vector machines. Just like support vectors, this naturally gives rise to the concept of support tokens. Furthermore, we show that LLMs can be interpreted as a stochastic process over the power set of the token space, providing a rigorous probabilistic framework for sequence modeling. We propose a Bayesian framework and derive a MAP estimation objective that requires only a minimal modification to standard LLM training: the addition of a smooth log-barrier penalty to the usual cross-entropy loss. We demonstrate that this provides more robust models without sacrificing out-of-sample accuracy and that it is straightforward to incorporate in practice.

Heterogeneity-Aware Client Selection Methodology For Efficient Federated Learning

Federated Learning (FL) enables a distributed client-server architecture where multiple clients collaboratively train a global Machine Learning (ML) model without sharing sensitive local data. However, FL often results in lower accuracy than traditional ML algorithms due to statistical heterogeneity across clients. Prior works attempt to address this by using model updates, such as loss and bias, from client models to select participants that can improve the global model's accuracy. However, these updates neither accurately represent a client's heterogeneity nor are their selection methods deterministic. We mitigate these limitations by introducing Terraform, a novel client selection methodology that uses gradient updates and a deterministic selection algorithm to select heterogeneous clients for retraining. This bi-pronged approach allows Terraform to achieve up to 47 percent higher accuracy over prior works. We further demonstrate its efficiency through comprehensive ablation studies and training time analyses, providing strong justification for the robustness of Terraform.

Transfer Learning via Latent Dependency Factor for Estimating PM 2.5

Air pollution, especially particulate matter 2.5 (PM 2.5), is a pressing concern for public health and is difficult to estimate in developing countries (data-poor regions) due to a lack of ground sensors. Transfer learning models can be leveraged to solve this problem, as they use alternate data sources to gain knowledge (i.e., data from data-rich regions). However, current transfer learning methodologies do not account for dependencies between the source and the target domains. We recognize this transfer problem as spatial transfer learning and propose a new feature named Latent Dependency Factor (LDF) that captures spatial and semantic dependencies of both domains and is subsequently added to the datasets. We generate LDF using a novel two-stage autoencoder model that learns from clusters of similar source and target domain data. Our experiments show that transfer models using LDF have a $19.34\%$ improvement over the best-performing baselines. We additionally support our experiments with qualitative results.

Predictive Inference in Multi-environment Scenarios

We address the challenge of constructing valid confidence intervals and sets in problems of prediction across multiple environments. We investigate two types of coverage suitable for these problems, extending the jackknife and split-conformal methods to show how to obtain distribution-free coverage in such non-traditional, hierarchical data-generating scenarios. Our contributions also include extensions for settings with non-real-valued responses and a theory of consistency for predictive inference in these general problems. We demonstrate a novel resizing method to adapt to problem difficulty, which applies both to existing approaches for predictive inference with hierarchical data and the methods we develop; this reduces prediction set sizes using limited information from the test environment, a key to the methods' practical performance, which we evaluate through neurochemical sensing and species classification datasets.

Predictive Inference with Weak Supervision

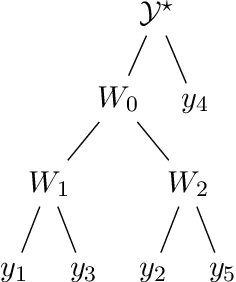
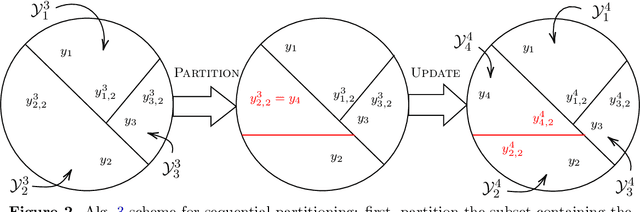
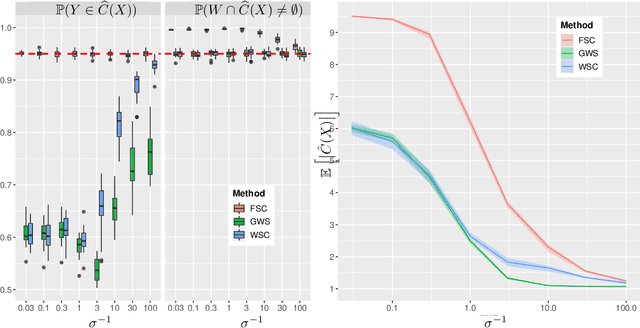
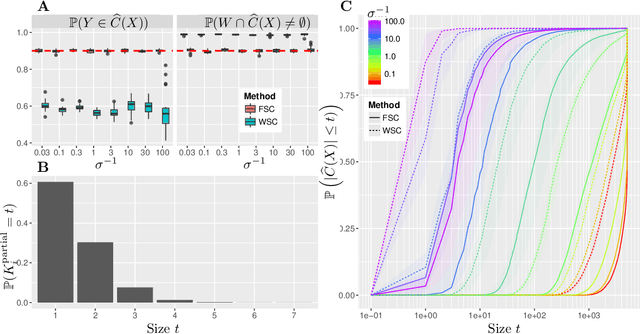
The expense of acquiring labels in large-scale statistical machine learning makes partially and weakly-labeled data attractive, though it is not always apparent how to leverage such data for model fitting or validation. We present a methodology to bridge the gap between partial supervision and validation, developing a conformal prediction framework to provide valid predictive confidence sets -- sets that cover a true label with a prescribed probability, independent of the underlying distribution -- using weakly labeled data. To do so, we introduce a (necessary) new notion of coverage and predictive validity, then develop several application scenarios, providing efficient algorithms for classification and several large-scale structured prediction problems. We corroborate the hypothesis that the new coverage definition allows for tighter and more informative (but valid) confidence sets through several experiments.

The $r$-value: evaluating stability with respect to distributional shifts

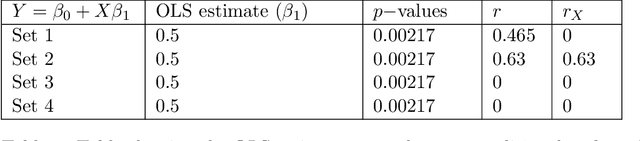
Common statistical measures of uncertainty like $p$-values and confidence intervals quantify the uncertainty due to sampling, that is, the uncertainty due to not observing the full population. In practice, populations change between locations and across time. This makes it difficult to gather knowledge that transfers across data sets. We propose a measure of uncertainty that quantifies the distributional uncertainty of a statistical estimand with respect to Kullback-Liebler divergence, that is, the sensitivity of the parameter under general distributional perturbations within a Kullback-Liebler divergence ball. If the signal-to-noise ratio is small, distributional uncertainty is a monotonous transformation of the signal-to-noise ratio. In general, however, it is a different concept and corresponds to a different research question. Further, we propose measures to estimate the stability of parameters with respect to directional or variable-specific shifts. We also demonstrate how the measure of distributional uncertainty can be used to prioritize data collection for better estimation of statistical parameters under shifted distribution. We evaluate the performance of the proposed measure in simulations and real data and show that it can elucidate the distributional (in-)stability of an estimator with respect to certain shifts and give more accurate estimates of parameters under shifted distribution only requiring to collect limited information from the shifted distribution.

Robust Validation: Confident Predictions Even When Distributions Shift

While the traditional viewpoint in machine learning and statistics assumes training and testing samples come from the same population, practice belies this fiction. One strategy---coming from robust statistics and optimization---is thus to build a model robust to distributional perturbations. In this paper, we take a different approach to describe procedures for robust predictive inference, where a model provides uncertainty estimates on its predictions rather than point predictions. We present a method that produces prediction sets (almost exactly) giving the right coverage level for any test distribution in an $f$-divergence ball around the training population. The method, based on conformal inference, achieves (nearly) valid coverage in finite samples, under only the condition that the training data be exchangeable. An essential component of our methodology is to estimate the amount of expected future data shift and build robustness to it; we develop estimators and prove their consistency for protection and validity of uncertainty estimates under shifts. By experimenting on several large-scale benchmark datasets, including Recht et al.'s CIFAR-v4 and ImageNet-V2 datasets, we provide complementary empirical results that highlight the importance of robust predictive validity.

Knowing what you know: valid confidence sets in multiclass and multilabel prediction

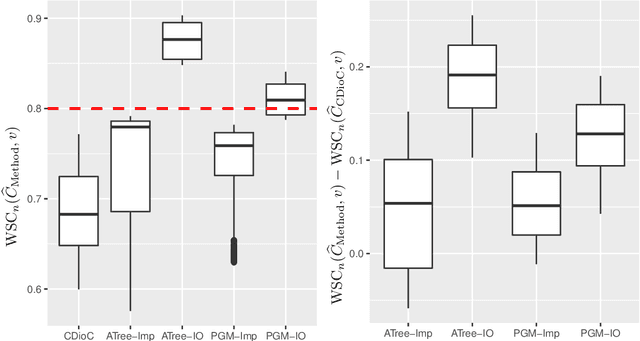
We develop conformal prediction methods for constructing valid predictive confidence sets in multiclass and multilabel problems without assumptions on the data generating distribution. A challenge here is that typical conformal prediction methods---which give marginal validity (coverage) guarantees---provide uneven coverage, in that they address easy examples at the expense of essentially ignoring difficult examples. By leveraging ideas from quantile regression, we build methods that always guarantee correct coverage but additionally provide (asymptotically optimal) conditional coverage for both multiclass and multilabel prediction problems. To address the potential challenge of exponentially large confidence sets in multilabel prediction, we build tree-structured classifiers that efficiently account for interactions between labels. Our methods can be bolted on top of any classification model---neural network, random forest, boosted tree---to guarantee its validity. We also provide an empirical evaluation suggesting the more robust coverage of our confidence sets.