Beyond Reweighting: On the Predictive Role of Covariate Shift in Effect Generalization

Many existing approaches to generalizing statistical inference amidst distribution shift operate under the covariate shift assumption, which posits that the conditional distribution of unobserved variables given observable ones is invariant across populations. However, recent empirical investigations have demonstrated that adjusting for shift in observed variables (covariate shift) is often insufficient for generalization. In other words, covariate shift does not typically ``explain away'' the distribution shift between settings. As such, addressing the unknown yet non-negligible shift in the unobserved variables given observed ones (conditional shift) is crucial for generalizable inference. In this paper, we present a series of empirical evidence from two large-scale multi-site replication studies to support a new role of covariate shift in ``predicting'' the strength of the unknown conditional shift. Analyzing 680 studies across 65 sites, we find that even though the conditional shift is non-negligible, its strength can often be bounded by that of the observable covariate shift. However, this pattern only emerges when the two sources of shifts are quantified by our proposed standardized, ``pivotal'' measures. We then interpret this phenomenon by connecting it to similar patterns that can be theoretically derived from a random distribution shift model. Finally, we demonstrate that exploiting the predictive role of covariate shift leads to reliable and efficient uncertainty quantification for target estimates in generalization tasks with partially observed data. Overall, our empirical and theoretical analyses suggest a new way to approach the problem of distributional shift, generalizability, and external validity.

Random Distribution Shift in Refugee Placement: Strategies for Building Robust Models

Algorithmic assignment of refugees and asylum seekers to locations within host countries has gained attention in recent years, with implementations in the US and Switzerland. These approaches use data on past arrivals to generate machine learning models that can be used (along with assignment algorithms) to match families to locations, with the goal of maximizing a policy-relevant integration outcome such as employment status after a certain duration. Existing implementations and research train models to predict the policy outcome directly, and use these predictions in the assignment procedure. However, the merits of this approach, particularly in non-stationary settings, has not been previously explored. This study proposes and compares three different modeling strategies: the standard approach described above, an approach that uses newer data and proxy outcomes, and a hybrid approach. We show that the hybrid approach is robust to both distribution shift and weak proxy relationships -- the failure points of the other two methods, respectively. We compare these approaches empirically using data on asylum seekers in the Netherlands. Surprisingly, we find that both the proxy and hybrid approaches out-perform the standard approach in practice. These insights support the development of a real-world recommendation tool currently used by NGOs and government agencies.

The $r$-value: evaluating stability with respect to distributional shifts

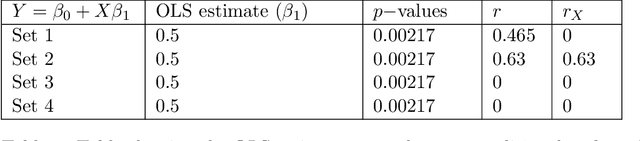
Common statistical measures of uncertainty like $p$-values and confidence intervals quantify the uncertainty due to sampling, that is, the uncertainty due to not observing the full population. In practice, populations change between locations and across time. This makes it difficult to gather knowledge that transfers across data sets. We propose a measure of uncertainty that quantifies the distributional uncertainty of a statistical estimand with respect to Kullback-Liebler divergence, that is, the sensitivity of the parameter under general distributional perturbations within a Kullback-Liebler divergence ball. If the signal-to-noise ratio is small, distributional uncertainty is a monotonous transformation of the signal-to-noise ratio. In general, however, it is a different concept and corresponds to a different research question. Further, we propose measures to estimate the stability of parameters with respect to directional or variable-specific shifts. We also demonstrate how the measure of distributional uncertainty can be used to prioritize data collection for better estimation of statistical parameters under shifted distribution. We evaluate the performance of the proposed measure in simulations and real data and show that it can elucidate the distributional (in-)stability of an estimator with respect to certain shifts and give more accurate estimates of parameters under shifted distribution only requiring to collect limited information from the shifted distribution.

backShift: Learning causal cyclic graphs from unknown shift interventions

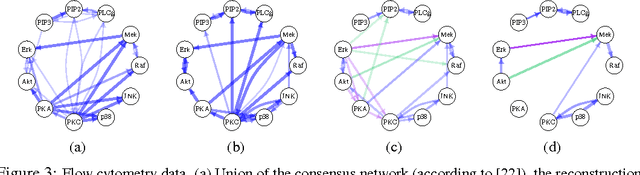
We propose a simple method to learn linear causal cyclic models in the presence of latent variables. The method relies on equilibrium data of the model recorded under a specific kind of interventions ("shift interventions"). The location and strength of these interventions do not have to be known and can be estimated from the data. Our method, called backShift, only uses second moments of the data and performs simple joint matrix diagonalization, applied to differences between covariance matrices. We give a sufficient and necessary condition for identifiability of the system, which is fulfilled almost surely under some quite general assumptions if and only if there are at least three distinct experimental settings, one of which can be pure observational data. We demonstrate the performance on some simulated data and applications in flow cytometry and financial time series. The code is made available as R-package backShift.