Building Trust: Foundations of Security, Safety and Transparency in AI

This paper explores the rapidly evolving ecosystem of publicly available AI models, and their potential implications on the security and safety landscape. As AI models become increasingly prevalent, understanding their potential risks and vulnerabilities is crucial. We review the current security and safety scenarios while highlighting challenges such as tracking issues, remediation, and the apparent absence of AI model lifecycle and ownership processes. Comprehensive strategies to enhance security and safety for both model developers and end-users are proposed. This paper aims to provide some of the foundational pieces for more standardized security, safety, and transparency in the development and operation of AI models and the larger open ecosystems and communities forming around them.

KinDEL: DNA-Encoded Library Dataset for Kinase Inhibitors

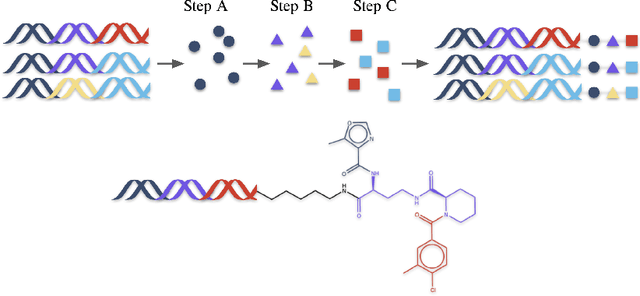
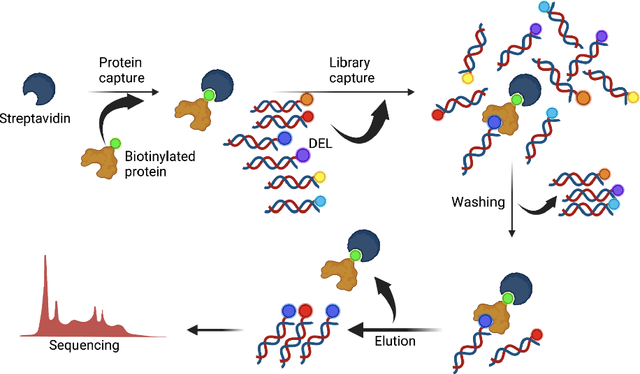
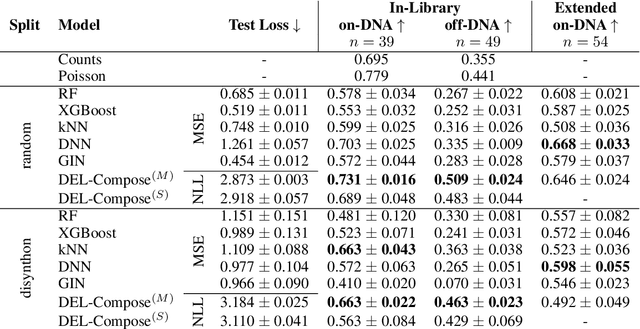
DNA-Encoded Libraries (DEL) are combinatorial small molecule libraries that offer an efficient way to characterize diverse chemical spaces. Selection experiments using DELs are pivotal to drug discovery efforts, enabling high-throughput screens for hit finding. However, limited availability of public DEL datasets hinders the advancement of computational techniques designed to process such data. To bridge this gap, we present KinDEL, one of the first large, publicly available DEL datasets on two kinases: Mitogen-Activated Protein Kinase 14 (MAPK14) and Discoidin Domain Receptor Tyrosine Kinase 1 (DDR1). Interest in this data modality is growing due to its ability to generate extensive supervised chemical data that densely samples around select molecular structures. Demonstrating one such application of the data, we benchmark different machine learning techniques to develop predictive models for hit identification; in particular, we highlight recent structure-based probabilistic approaches. Finally, we provide biophysical assay data, both on- and off-DNA, to validate our models on a smaller subset of molecules. Data and code for our benchmarks can be found at: https://github.com/insitro/kindel.

Learning Insulin-Glucose Dynamics in the Wild

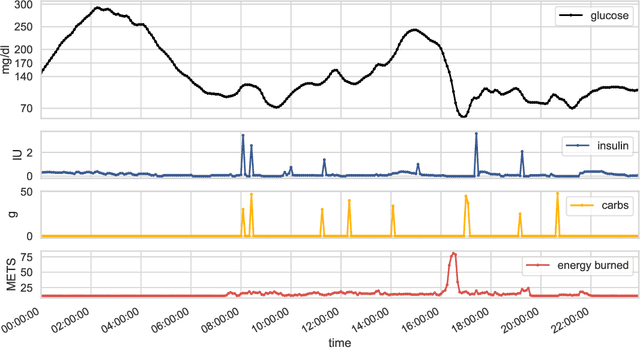
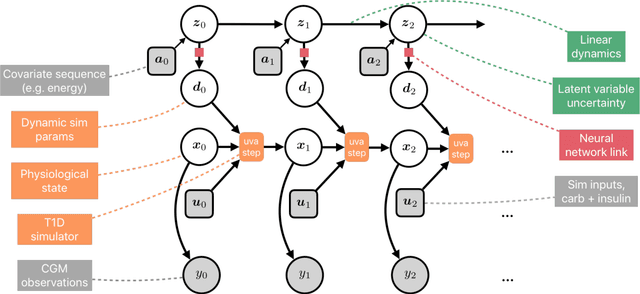
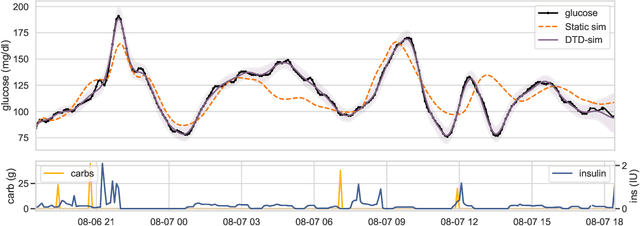
We develop a new model of insulin-glucose dynamics for forecasting blood glucose in type 1 diabetics. We augment an existing biomedical model by introducing time-varying dynamics driven by a machine learning sequence model. Our model maintains a physiologically plausible inductive bias and clinically interpretable parameters -- e.g., insulin sensitivity -- while inheriting the flexibility of modern pattern recognition algorithms. Critical to modeling success are the flexible, but structured representations of subject variability with a sequence model. In contrast, less constrained models like the LSTM fail to provide reliable or physiologically plausible forecasts. We conduct an extensive empirical study. We show that allowing biomedical model dynamics to vary in time improves forecasting at long time horizons, up to six hours, and produces forecasts consistent with the physiological effects of insulin and carbohydrates.

Improving Reproducibility in Machine Learning Research (A Report from the NeurIPS 2019 Reproducibility Program)

One of the challenges in machine learning research is to ensure that presented and published results are sound and reliable. Reproducibility, that is obtaining similar results as presented in a paper or talk, using the same code and data (when available), is a necessary step to verify the reliability of research findings. Reproducibility is also an important step to promote open and accessible research, thereby allowing the scientific community to quickly integrate new findings and convert ideas to practice. Reproducibility also promotes the use of robust experimental workflows, which potentially reduce unintentional errors. In 2019, the Neural Information Processing Systems (NeurIPS) conference, the premier international conference for research in machine learning, introduced a reproducibility program, designed to improve the standards across the community for how we conduct, communicate, and evaluate machine learning research. The program contained three components: a code submission policy, a community-wide reproducibility challenge, and the inclusion of the Machine Learning Reproducibility checklist as part of the paper submission process. In this paper, we describe each of these components, how it was deployed, as well as what we were able to learn from this initiative.

A Unified Framework for Long Range and Cold Start Forecasting of Seasonal Profiles in Time Series

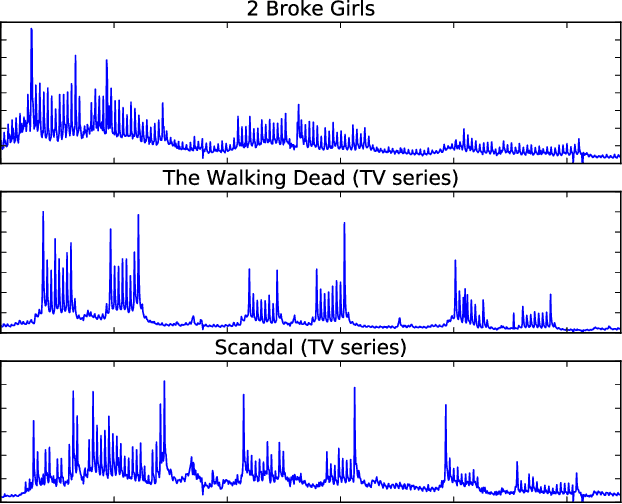
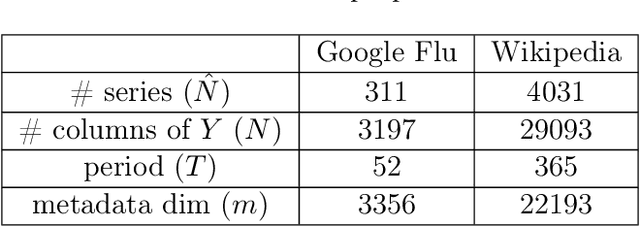
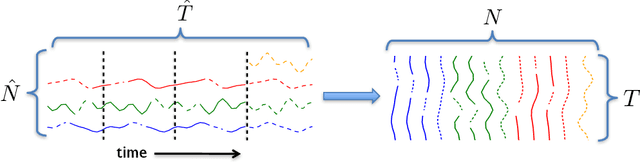
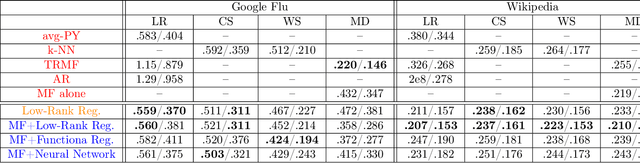
Providing long-range forecasts is a fundamental challenge in time series modeling, which is only compounded by the challenge of having to form such forecasts when a time series has never previously been observed. The latter challenge is the time series version of the cold-start problem seen in recommender systems which, to our knowledge, has not been addressed in previous work. A similar problem occurs when a long range forecast is required after only observing a small number of time points --- a warm start forecast. With these aims in mind, we focus on forecasting seasonal profiles---or baseline demand---for periods on the order of a year in three cases: the long range case with multiple previously observed seasonal profiles, the cold start case with no previous observed seasonal profiles, and the warm start case with only a single partially observed profile. Classical time series approaches that perform iterated step-ahead forecasts based on previous observations struggle to provide accurate long range predictions; in settings with little to no observed data, such approaches are simply not applicable. Instead, we present a straightforward framework which combines ideas from high-dimensional regression and matrix factorization on a carefully constructed data matrix. Key to our formulation and resulting performance is leveraging (1) repeated patterns over fixed periods of time and across series, and (2) metadata associated with the individual series; without this additional data, the cold-start/warm-start problems are nearly impossible to solve. We demonstrate that our framework can accurately forecast an array of seasonal profiles on multiple large scale datasets.

Interpretable VAEs for nonlinear group factor analysis

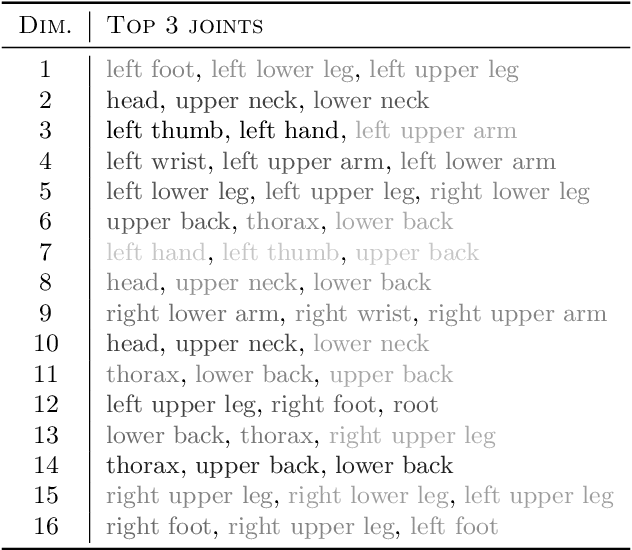
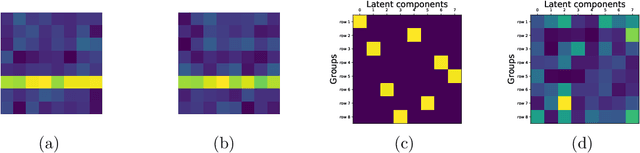
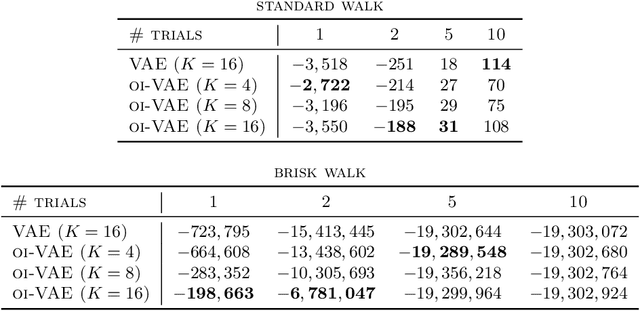
Deep generative models have recently yielded encouraging results in producing subjectively realistic samples of complex data. Far less attention has been paid to making these generative models interpretable. In many scenarios, ranging from scientific applications to finance, the observed variables have a natural grouping. It is often of interest to understand systems of interaction amongst these groups, and latent factor models (LFMs) are an attractive approach. However, traditional LFMs are limited by assuming a linear correlation structure. We present an output interpretable VAE (oi-VAE) for grouped data that models complex, nonlinear latent-to-observed relationships. We combine a structured VAE comprised of group-specific generators with a sparsity-inducing prior. We demonstrate that oi-VAE yields meaningful notions of interpretability in the analysis of motion capture and MEG data. We further show that in these situations, the regularization inherent to oi-VAE can actually lead to improved generalization and learned generative processes.

Neural Granger Causality for Nonlinear Time Series

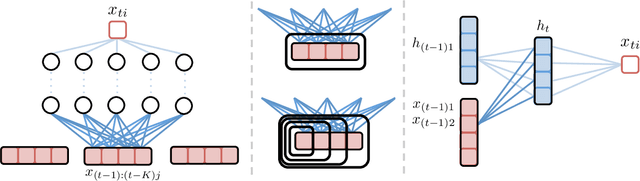
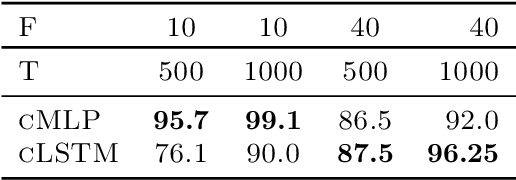
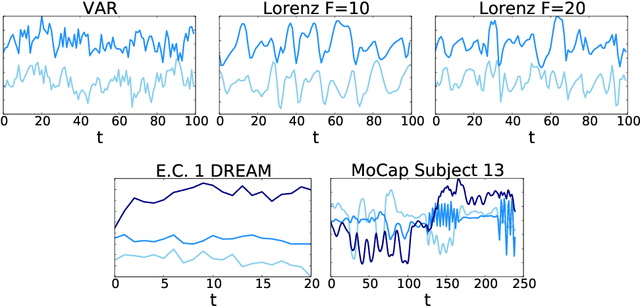
While most classical approaches to Granger causality detection assume linear dynamics, many interactions in applied domains, like neuroscience and genomics, are inherently nonlinear. In these cases, using linear models may lead to inconsistent estimation of Granger causal interactions. We propose a class of nonlinear methods by applying structured multilayer perceptrons (MLPs) or recurrent neural networks (RNNs) combined with sparsity-inducing penalties on the weights. By encouraging specific sets of weights to be zero---in particular through the use of convex group-lasso penalties---we can extract the Granger causal structure. To further contrast with traditional approaches, our framework naturally enables us to efficiently capture long-range dependencies between series either via our RNNs or through an automatic lag selection in the MLP. We show that our neural Granger causality methods outperform state-of-the-art nonlinear Granger causality methods on the DREAM3 challenge data. This data consists of nonlinear gene expression and regulation time courses with only a limited number of time points. The successes we show in this challenging dataset provide a powerful example of how deep learning can be useful in cases that go beyond prediction on large datasets. We likewise demonstrate our methods in detecting nonlinear interactions in a human motion capture dataset.

Expectation-Maximization for Learning Determinantal Point Processes

A determinantal point process (DPP) is a probabilistic model of set diversity compactly parameterized by a positive semi-definite kernel matrix. To fit a DPP to a given task, we would like to learn the entries of its kernel matrix by maximizing the log-likelihood of the available data. However, log-likelihood is non-convex in the entries of the kernel matrix, and this learning problem is conjectured to be NP-hard. Thus, previous work has instead focused on more restricted convex learning settings: learning only a single weight for each row of the kernel matrix, or learning weights for a linear combination of DPPs with fixed kernel matrices. In this work we propose a novel algorithm for learning the full kernel matrix. By changing the kernel parameterization from matrix entries to eigenvalues and eigenvectors, and then lower-bounding the likelihood in the manner of expectation-maximization algorithms, we obtain an effective optimization procedure. We test our method on a real-world product recommendation task, and achieve relative gains of up to 16.5% in test log-likelihood compared to the naive approach of maximizing likelihood by projected gradient ascent on the entries of the kernel matrix.

Bayesian Nonparametric Covariance Regression

Although there is a rich literature on methods for allowing the variance in a univariate regression model to vary with predictors, time and other factors, relatively little has been done in the multivariate case. Our focus is on developing a class of nonparametric covariance regression models, which allow an unknown p x p covariance matrix to change flexibly with predictors. The proposed modeling framework induces a prior on a collection of covariance matrices indexed by predictors through priors for predictor-dependent loadings matrices in a factor model. In particular, the predictor-dependent loadings are characterized as a sparse combination of a collection of unknown dictionary functions (e.g, Gaussian process random functions). The induced covariance is then a regularized quadratic function of these dictionary elements. Our proposed framework leads to a highly-flexible, but computationally tractable formulation with simple conjugate posterior updates that can readily handle missing data. Theoretical properties are discussed and the methods are illustrated through simulations studies and an application to the Google Flu Trends data.