A Unified Framework for Long Range and Cold Start Forecasting of Seasonal Profiles in Time Series

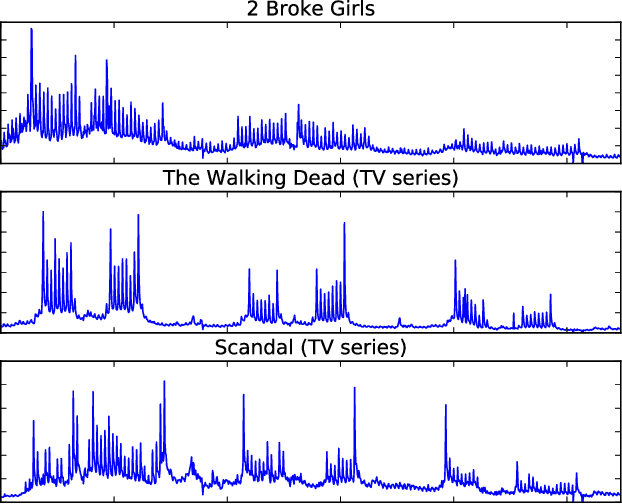
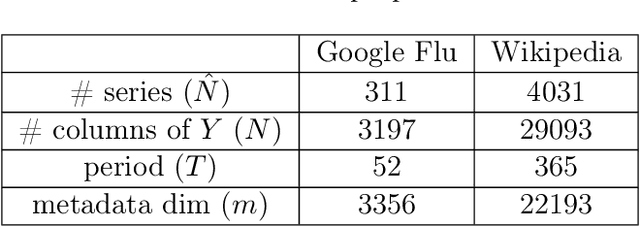
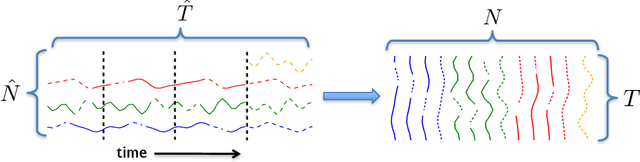
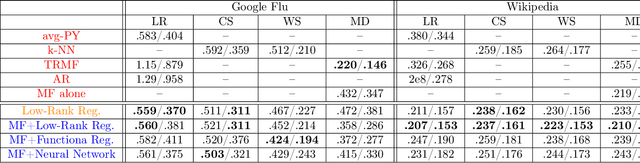
Providing long-range forecasts is a fundamental challenge in time series modeling, which is only compounded by the challenge of having to form such forecasts when a time series has never previously been observed. The latter challenge is the time series version of the cold-start problem seen in recommender systems which, to our knowledge, has not been addressed in previous work. A similar problem occurs when a long range forecast is required after only observing a small number of time points --- a warm start forecast. With these aims in mind, we focus on forecasting seasonal profiles---or baseline demand---for periods on the order of a year in three cases: the long range case with multiple previously observed seasonal profiles, the cold start case with no previous observed seasonal profiles, and the warm start case with only a single partially observed profile. Classical time series approaches that perform iterated step-ahead forecasts based on previous observations struggle to provide accurate long range predictions; in settings with little to no observed data, such approaches are simply not applicable. Instead, we present a straightforward framework which combines ideas from high-dimensional regression and matrix factorization on a carefully constructed data matrix. Key to our formulation and resulting performance is leveraging (1) repeated patterns over fixed periods of time and across series, and (2) metadata associated with the individual series; without this additional data, the cold-start/warm-start problems are nearly impossible to solve. We demonstrate that our framework can accurately forecast an array of seasonal profiles on multiple large scale datasets.

An Interpretable and Sparse Neural Network Model for Nonlinear Granger Causality Discovery

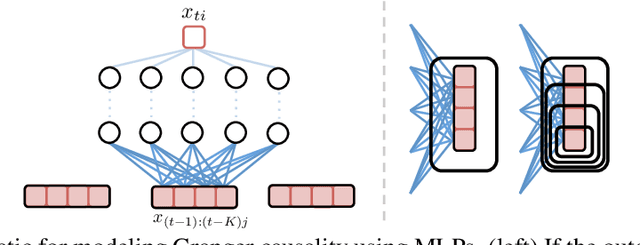
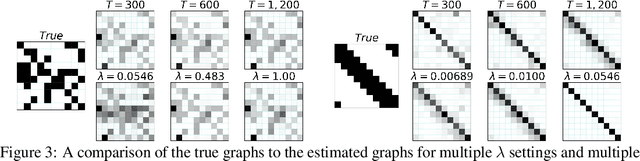
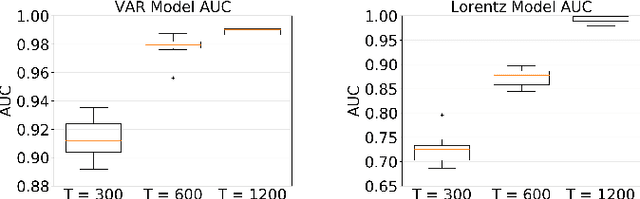
While most classical approaches to Granger causality detection repose upon linear time series assumptions, many interactions in neuroscience and economics applications are nonlinear. We develop an approach to nonlinear Granger causality detection using multilayer perceptrons where the input to the network is the past time lags of all series and the output is the future value of a single series. A sufficient condition for Granger non-causality in this setting is that all of the outgoing weights of the input data, the past lags of a series, to the first hidden layer are zero. For estimation, we utilize a group lasso penalty to shrink groups of input weights to zero. We also propose a hierarchical penalty for simultaneous Granger causality and lag estimation. We validate our approach on simulated data from both a sparse linear autoregressive model and the sparse and nonlinear Lorenz-96 model.

An Efficient ADMM Algorithm for Structural Break Detection in Multivariate Time Series

We present an efficient alternating direction method of multipliers (ADMM) algorithm for segmenting a multivariate non-stationary time series with structural breaks into stationary regions. We draw from recent work where the series is assumed to follow a vector autoregressive model within segments and a convex estimation procedure may be formulated using group fused lasso penalties. Our ADMM approach first splits the convex problem into a global quadratic program and a simple group lasso proximal update. We show that the global problem may be parallelized over rows of the time dependent transition matrices and furthermore that each subproblem may be rewritten in a form identical to the log-likelihood of a Gaussian state space model. Consequently, we develop a Kalman smoothing algorithm to solve the global update in time linear in the length of the series.

Neural Granger Causality for Nonlinear Time Series

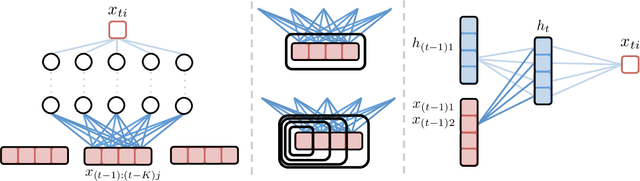
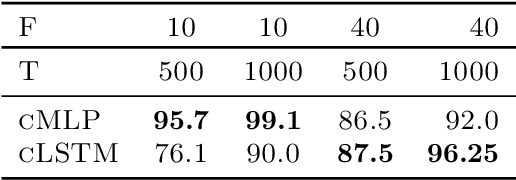
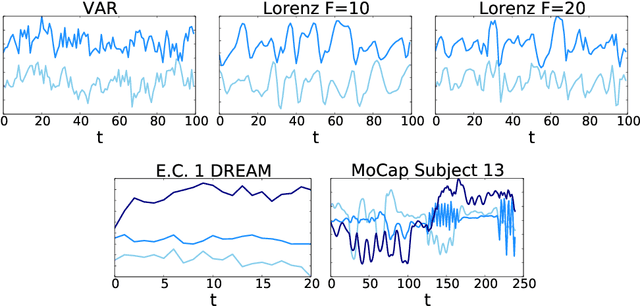
While most classical approaches to Granger causality detection assume linear dynamics, many interactions in applied domains, like neuroscience and genomics, are inherently nonlinear. In these cases, using linear models may lead to inconsistent estimation of Granger causal interactions. We propose a class of nonlinear methods by applying structured multilayer perceptrons (MLPs) or recurrent neural networks (RNNs) combined with sparsity-inducing penalties on the weights. By encouraging specific sets of weights to be zero---in particular through the use of convex group-lasso penalties---we can extract the Granger causal structure. To further contrast with traditional approaches, our framework naturally enables us to efficiently capture long-range dependencies between series either via our RNNs or through an automatic lag selection in the MLP. We show that our neural Granger causality methods outperform state-of-the-art nonlinear Granger causality methods on the DREAM3 challenge data. This data consists of nonlinear gene expression and regulation time courses with only a limited number of time points. The successes we show in this challenging dataset provide a powerful example of how deep learning can be useful in cases that go beyond prediction on large datasets. We likewise demonstrate our methods in detecting nonlinear interactions in a human motion capture dataset.

Streaming Variational Inference for Bayesian Nonparametric Mixture Models

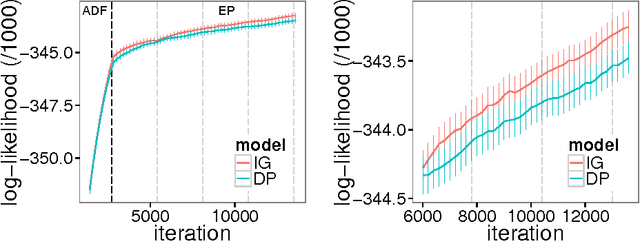
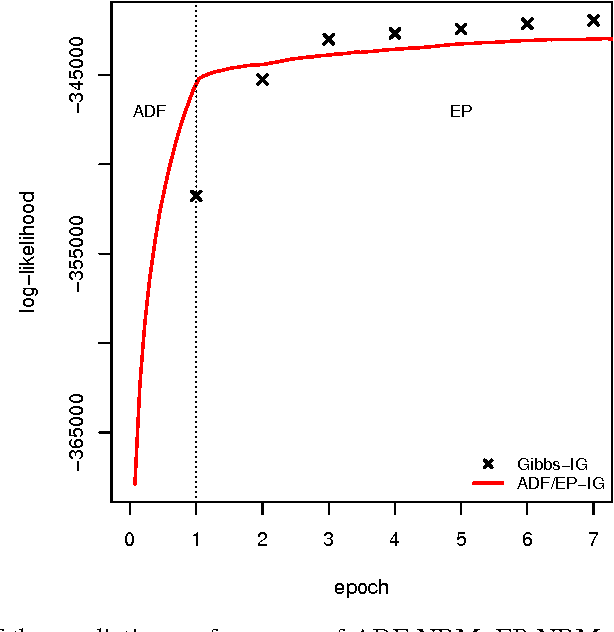
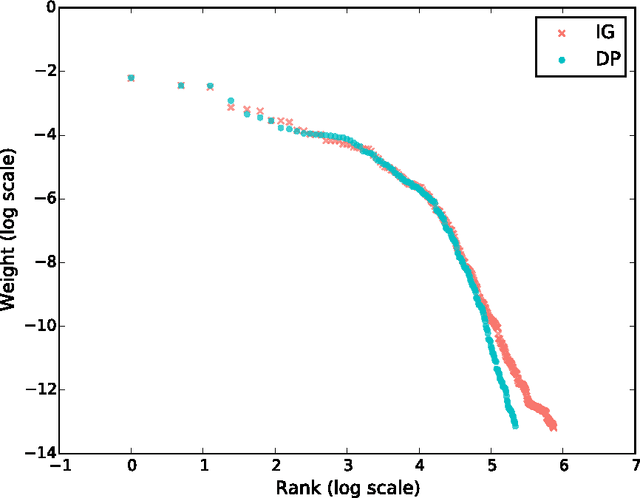
In theory, Bayesian nonparametric (BNP) models are well suited to streaming data scenarios due to their ability to adapt model complexity with the observed data. Unfortunately, such benefits have not been fully realized in practice; existing inference algorithms are either not applicable to streaming applications or not extensible to BNP models. For the special case of Dirichlet processes, streaming inference has been considered. However, there is growing interest in more flexible BNP models building on the class of normalized random measures (NRMs). We work within this general framework and present a streaming variational inference algorithm for NRM mixture models. Our algorithm is based on assumed density filtering (ADF), leading straightforwardly to expectation propagation (EP) for large-scale batch inference as well. We demonstrate the efficacy of the algorithm on clustering documents in large, streaming text corpora.