Spectral Differential Network Analysis for High-Dimensional Time Series

Spectral networks derived from multivariate time series data arise in many domains, from brain science to Earth science. Often, it is of interest to study how these networks change under different conditions. For instance, to better understand epilepsy, it would be interesting to capture the changes in the brain connectivity network as a patient experiences a seizure, using electroencephalography data. A common approach relies on estimating the networks in each condition and calculating their difference. Such estimates may behave poorly in high dimensions as the networks themselves may not be sparse in structure while their difference may be. We build upon this observation to develop an estimator of the difference in inverse spectral densities across two conditions. Using an L1 penalty on the difference, consistency is established by only requiring the difference to be sparse. We illustrate the method on synthetic data experiments, on experiments with electroencephalography data, and on experiments with optogentic stimulation and micro-electrocorticography data.

An Asymptotically Optimal Coordinate Descent Algorithm for Learning Bayesian Networks from Gaussian Models

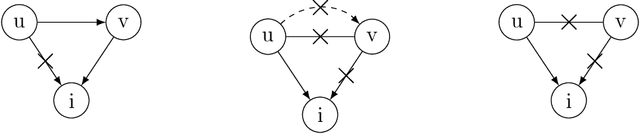
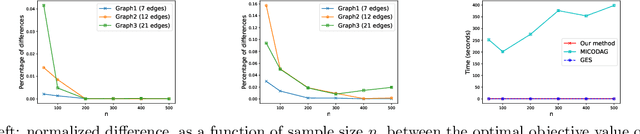
This paper studies the problem of learning Bayesian networks from continuous observational data, generated according to a linear Gaussian structural equation model. We consider an $\ell_0$-penalized maximum likelihood estimator for this problem which is known to have favorable statistical properties but is computationally challenging to solve, especially for medium-sized Bayesian networks. We propose a new coordinate descent algorithm to approximate this estimator and prove several remarkable properties of our procedure: the algorithm converges to a coordinate-wise minimum, and despite the non-convexity of the loss function, as the sample size tends to infinity, the objective value of the coordinate descent solution converges to the optimal objective value of the $\ell_0$-penalized maximum likelihood estimator. Finite-sample optimality and statistical consistency guarantees are also established. To the best of our knowledge, our proposal is the first coordinate descent procedure endowed with optimality and statistical guarantees in the context of learning Bayesian networks. Numerical experiments on synthetic and real data demonstrate that our coordinate descent method can obtain near-optimal solutions while being scalable.

Principal component analysis balancing prediction and approximation accuracy for spatial data

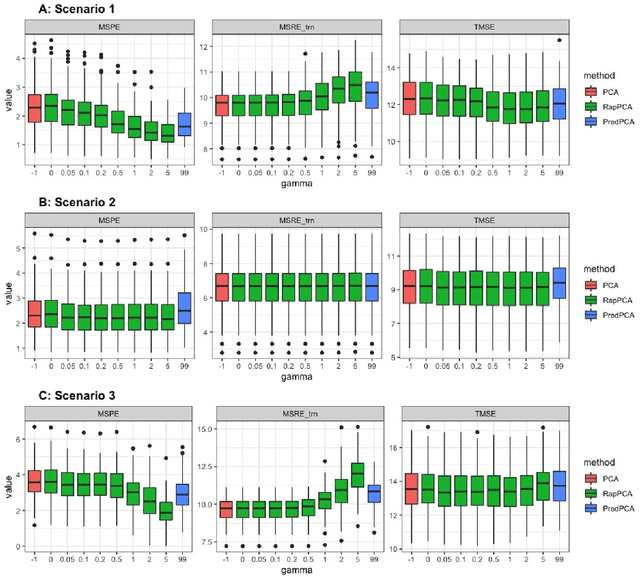
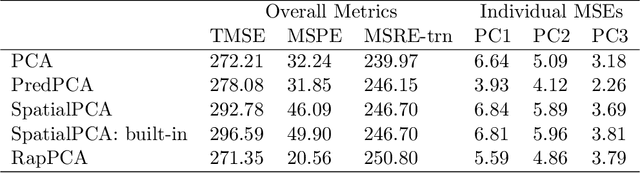
Dimension reduction is often the first step in statistical modeling or prediction of multivariate spatial data. However, most existing dimension reduction techniques do not account for the spatial correlation between observations and do not take the downstream modeling task into consideration when finding the lower-dimensional representation. We formalize the closeness of approximation to the original data and the utility of lower-dimensional scores for downstream modeling as two complementary, sometimes conflicting, metrics for dimension reduction. We illustrate how existing methodologies fall into this framework and propose a flexible dimension reduction algorithm that achieves the optimal trade-off. We derive a computationally simple form for our algorithm and illustrate its performance through simulation studies, as well as two applications in air pollution modeling and spatial transcriptomics.

Variable importance measure for spatial machine learning models with application to air pollution exposure prediction

Exposure assessment is fundamental to air pollution cohort studies. The objective is to predict air pollution exposures for study subjects at locations without data in order to optimize our ability to learn about health effects of air pollution. In addition to generating accurate predictions to minimize exposure measurement error, understanding the mechanism captured by the model is another crucial aspect that may not always be straightforward due to the complex nature of machine learning methods, as well as the lack of unifying notions of variable importance. This is further complicated in air pollution modeling by the presence of spatial correlation. We tackle these challenges in two datasets: sulfur (S) from regulatory United States national PM2.5 sub-species data and ultrafine particles (UFP) from a new Seattle-area traffic-related air pollution dataset. Our key contribution is a leave-one-out approach for variable importance that leads to interpretable and comparable measures for a broad class of models with separable mean and covariance components. We illustrate our approach with several spatial machine learning models, and it clearly highlights the difference in model mechanisms, even for those producing similar predictions. We leverage insights from this variable importance measure to assess the relative utilities of two exposure models for S and UFP that have similar out-of-sample prediction accuracies but appear to draw on different types of spatial information to make predictions.

Learning Directed Acyclic Graphs from Partial Orderings

Directed acyclic graphs (DAGs) are commonly used to model causal relationships among random variables. In general, learning the DAG structure is both computationally and statistically challenging. Moreover, without additional information, the direction of edges may not be estimable from observational data. In contrast, given a complete causal ordering of the variables, the problem can be solved efficiently, even in high dimensions. In this paper, we consider the intermediate problem of learning DAGs when a partial causal ordering of variables is available. We propose a general estimation framework for leveraging the partial ordering and present efficient estimation algorithms for low- and high-dimensional problems. The advantages of the proposed framework are illustrated via numerical studies.

A Penalized Poisson Likelihood Approach to High-Dimensional Semi-Parametric Inference for Doubly-Stochastic Point Processes

Doubly-stochastic point processes model the occurrence of events over a spatial domain as an inhomogeneous Poisson process conditioned on the realization of a random intensity function. They are flexible tools for capturing spatial heterogeneity and dependence. However, implementations of doubly-stochastic spatial models are computationally demanding, often have limited theoretical guarantee, and/or rely on restrictive assumptions. We propose a penalized regression method for estimating covariate effects in doubly-stochastic point processes that is computationally efficient and does not require a parametric form or stationarity of the underlying intensity. We establish the consistency and asymptotic normality of the proposed estimator, and develop a covariance estimator that leads to a conservative statistical inference procedure. A simulation study shows the validity of our approach under less restrictive assumptions on the data generating mechanism, and an application to Seattle crime data demonstrates better prediction accuracy compared with existing alternatives.

Estimation of High-Dimensional Markov-Switching VAR Models with an Approximate EM Algorithm

Regime shifts in high-dimensional time series arise naturally in many applications, from neuroimaging to finance. This problem has received considerable attention in low-dimensional settings, with both Bayesian and frequentist methods used extensively for parameter estimation. The EM algorithm is a particularly popular strategy for parameter estimation in low-dimensional settings, although the statistical properties of the resulting estimates have not been well understood. Furthermore, its extension to high-dimensional time series has proved challenging. To overcome these challenges, in this paper we propose an approximate EM algorithm for Markov-switching VAR models that leads to efficient computation and also facilitates the investigation of asymptotic properties of the resulting parameter estimates. We establish the consistency of the proposed EM algorithm in high dimensions and investigate its performance via simulation studies.

Joint Estimation and Inference for Multi-Experiment Networks of High-Dimensional Point Processes

Modern high-dimensional point process data, especially those from neuroscience experiments, often involve observations from multiple conditions and/or experiments. Networks of interactions corresponding to these conditions are expected to share many edges, but also exhibit unique, condition-specific ones. However, the degree of similarity among the networks from different conditions is generally unknown. Existing approaches for multivariate point processes do not take these structures into account and do not provide inference for jointly estimated networks. To address these needs, we propose a joint estimation procedure for networks of high-dimensional point processes that incorporates easy-to-compute weights in order to data-adaptively encourage similarity between the estimated networks. We also propose a powerful hierarchical multiple testing procedure for edges of all estimated networks, which takes into account the data-driven similarity structure of the multi-experiment networks. Compared to conventional multiple testing procedures, our proposed procedure greatly reduces the number of tests and results in improved power, while tightly controlling the family-wise error rate. Unlike existing procedures, our method is also free of assumptions on dependency between tests, offers flexibility on p-values calculated along the hierarchy, and is robust to misspecification of the hierarchical structure. We verify our theoretical results via simulation studies and demonstrate the application of the proposed procedure using neuronal spike train data.

Causal Discovery in High-Dimensional Point Process Networks with Hidden Nodes

Thanks to technological advances leading to near-continuous time observations, emerging multivariate point process data offer new opportunities for causal discovery. However, a key obstacle in achieving this goal is that many relevant processes may not be observed in practice. Naive estimation approaches that ignore these hidden variables can generate misleading results because of the unadjusted confounding. To plug this gap, we propose a deconfounding procedure to estimate high-dimensional point process networks with only a subset of the nodes being observed. Our method allows flexible connections between the observed and unobserved processes. It also allows the number of unobserved processes to be unknown and potentially larger than the number of observed nodes. Theoretical analyses and numerical studies highlight the advantages of the proposed method in identifying causal interactions among the observed processes.

Interaction Models and Generalized Score Matching for Compositional Data

Applications such as the analysis of microbiome data have led to renewed interest in statistical methods for compositional data, i.e., multivariate data in the form of probability vectors that contain relative proportions. In particular, there is considerable interest in modeling interactions among such relative proportions. To this end we propose a class of exponential family models that accommodate general patterns of pairwise interaction while being supported on the probability simplex. Special cases include the family of Dirichlet distributions as well as Aitchison's additive logistic normal distributions. Generally, the distributions we consider have a density that features a difficult to compute normalizing constant. To circumvent this issue, we design effective estimation methods based on generalized versions of score matching. A high-dimensional analysis of our estimation methods shows that the simplex domain is handled as efficiently as previously studied full-dimensional domains.