An Asymptotically Optimal Coordinate Descent Algorithm for Learning Bayesian Networks from Gaussian Models

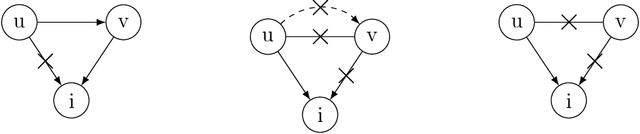
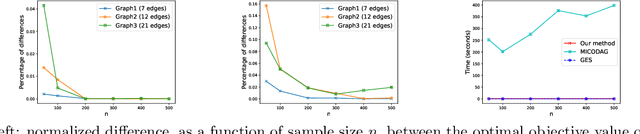
This paper studies the problem of learning Bayesian networks from continuous observational data, generated according to a linear Gaussian structural equation model. We consider an $\ell_0$-penalized maximum likelihood estimator for this problem which is known to have favorable statistical properties but is computationally challenging to solve, especially for medium-sized Bayesian networks. We propose a new coordinate descent algorithm to approximate this estimator and prove several remarkable properties of our procedure: the algorithm converges to a coordinate-wise minimum, and despite the non-convexity of the loss function, as the sample size tends to infinity, the objective value of the coordinate descent solution converges to the optimal objective value of the $\ell_0$-penalized maximum likelihood estimator. Finite-sample optimality and statistical consistency guarantees are also established. To the best of our knowledge, our proposal is the first coordinate descent procedure endowed with optimality and statistical guarantees in the context of learning Bayesian networks. Numerical experiments on synthetic and real data demonstrate that our coordinate descent method can obtain near-optimal solutions while being scalable.

On the convex hull of convex quadratic optimization problems with indicators

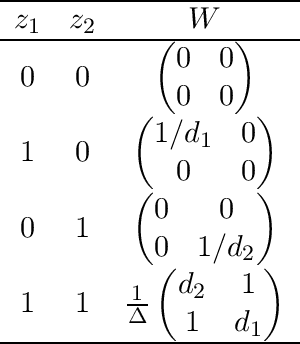
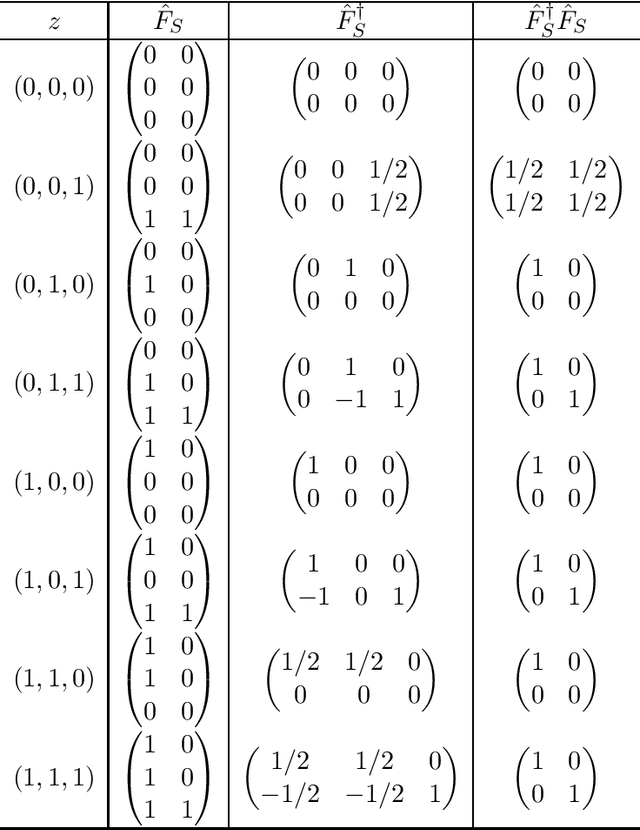
We consider the convex quadratic optimization problem with indicator variables and arbitrary constraints on the indicators. We show that a convex hull description of the associated mixed-integer set in an extended space with a quadratic number of additional variables consists of a single positive semidefinite constraint (explicitly stated) and linear constraints. In particular, convexification of this class of problems reduces to describing a polyhedral set in an extended formulation. We also give descriptions in the original space of variables: we provide a description based on an infinite number of conic-quadratic inequalities, which are "finitely generated." In particular, it is possible to characterize whether a given inequality is necessary to describe the convex-hull. The new theory presented here unifies several previously established results, and paves the way toward utilizing polyhedral methods to analyze the convex hull of mixed-integer nonlinear sets.

Integer Programming for Learning Directed Acyclic Graphs from Continuous Data

Learning directed acyclic graphs (DAGs) from data is a challenging task both in theory and in practice, because the number of possible DAGs scales superexponentially with the number of nodes. In this paper, we study the problem of learning an optimal DAG from continuous observational data. We cast this problem in the form of a mathematical programming model which can naturally incorporate a super-structure in order to reduce the set of possible candidate DAGs. We use the penalized negative log-likelihood score function with both $\ell_0$ and $\ell_1$ regularizations and propose a new mixed-integer quadratic optimization (MIQO) model, referred to as a layered network (LN) formulation. The LN formulation is a compact model, which enjoys as tight an optimal continuous relaxation value as the stronger but larger formulations under a mild condition. Computational results indicate that the proposed formulation outperforms existing mathematical formulations and scales better than available algorithms that can solve the same problem with only $\ell_1$ regularization. In particular, the LN formulation clearly outperforms existing methods in terms of computational time needed to find an optimal DAG in the presence of a sparse super-structure.