Stability Regularized Cross-Validation

We revisit the problem of ensuring strong test-set performance via cross-validation. Motivated by the generalization theory literature, we propose a nested k-fold cross-validation scheme that selects hyperparameters by minimizing a weighted sum of the usual cross-validation metric and an empirical model-stability measure. The weight on the stability term is itself chosen via a nested cross-validation procedure. This reduces the risk of strong validation set performance and poor test set performance due to instability. We benchmark our procedure on a suite of 13 real-world UCI datasets, and find that, compared to k-fold cross-validation over the same hyperparameters, it improves the out-of-sample MSE for sparse ridge regression and CART by 4% on average, but has no impact on XGBoost. This suggests that for interpretable and unstable models, such as sparse regression and CART, our approach is a viable and computationally affordable method for improving test-set performance.

Mixed-Integer Optimization for Responsible Machine Learning

In the last few decades, Machine Learning (ML) has achieved significant success across domains ranging from healthcare, sustainability, and the social sciences, to criminal justice and finance. But its deployment in increasingly sophisticated, critical, and sensitive areas affecting individuals, the groups they belong to, and society as a whole raises critical concerns around fairness, transparency, robustness, and privacy, among others. As the complexity and scale of ML systems and of the settings in which they are deployed grow, so does the need for responsible ML methods that address these challenges while providing guaranteed performance in deployment. Mixed-integer optimization (MIO) offers a powerful framework for embedding responsible ML considerations directly into the learning process while maintaining performance. For example, it enables learning of inherently transparent models that can conveniently incorporate fairness or other domain specific constraints. This tutorial paper provides an accessible and comprehensive introduction to this topic discussing both theoretical and practical aspects. It outlines some of the core principles of responsible ML, their importance in applications, and the practical utility of MIO for building ML models that align with these principles. Through examples and mathematical formulations, it illustrates practical strategies and available tools for efficiently solving MIO problems for responsible ML. It concludes with a discussion on current limitations and open research questions, providing suggestions for future work.

Fair and Accurate Regression: Strong Formulations and Algorithms

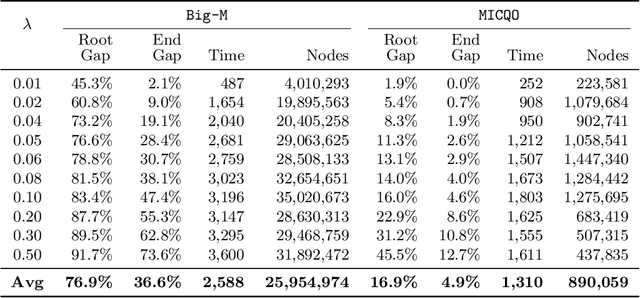
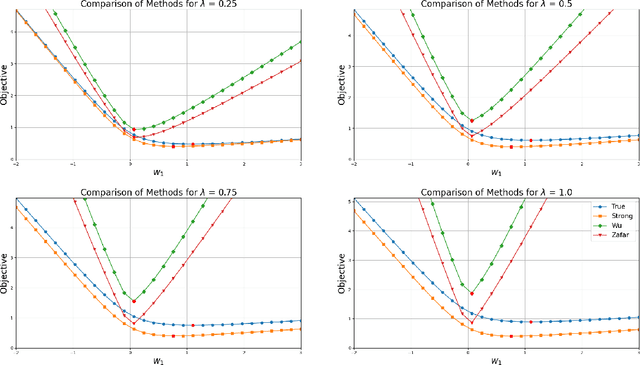
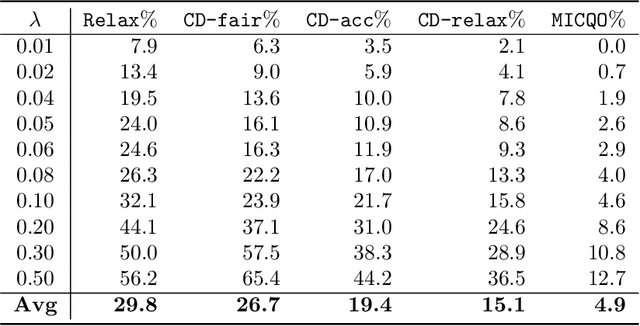
This paper introduces mixed-integer optimization methods to solve regression problems that incorporate fairness metrics. We propose an exact formulation for training fair regression models. To tackle this computationally hard problem, we study the polynomially-solvable single-factor and single-observation subproblems as building blocks and derive their closed convex hull descriptions. Strong formulations obtained for the general fair regression problem in this manner are utilized to solve the problem with a branch-and-bound algorithm exactly or as a relaxation to produce fair and accurate models rapidly. Moreover, to handle large-scale instances, we develop a coordinate descent algorithm motivated by the convex-hull representation of the single-factor fair regression problem to improve a given solution efficiently. Numerical experiments conducted on fair least squares and fair logistic regression problems show competitive statistical performance with state-of-the-art methods while significantly reducing training times.

Robust support vector machines via conic optimization

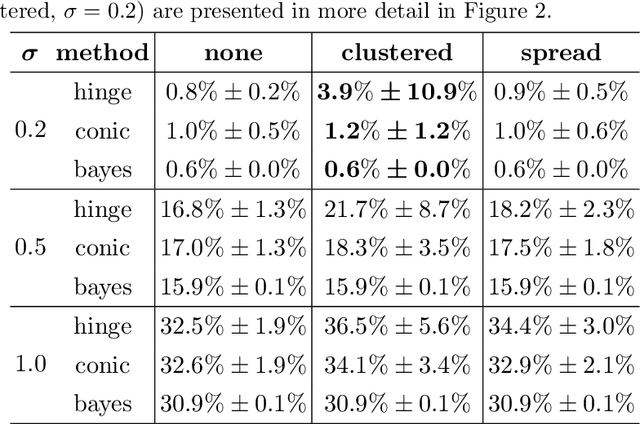
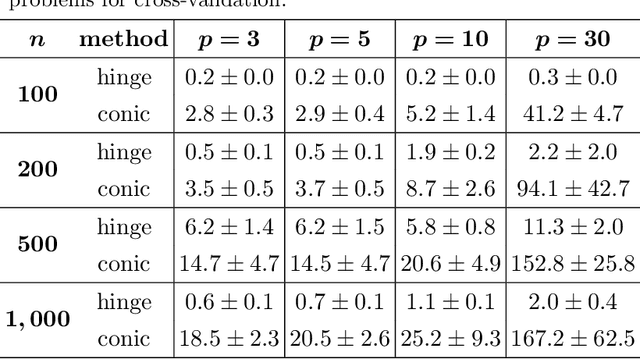
We consider the problem of learning support vector machines robust to uncertainty. It has been established in the literature that typical loss functions, including the hinge loss, are sensible to data perturbations and outliers, thus performing poorly in the setting considered. In contrast, using the 0-1 loss or a suitable non-convex approximation results in robust estimators, at the expense of large computational costs. In this paper we use mixed-integer optimization techniques to derive a new loss function that better approximates the 0-1 loss compared with existing alternatives, while preserving the convexity of the learning problem. In our computational results, we show that the proposed estimator is competitive with the standard SVMs with the hinge loss in outlier-free regimes and better in the presence of outliers.

Density Matrix Emulation of Quantum Recurrent Neural Networks for Multivariate Time Series Prediction

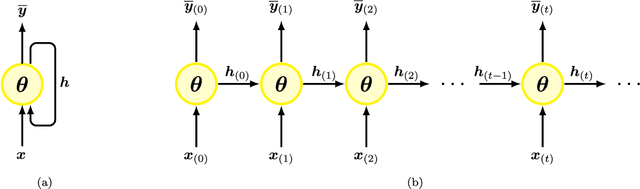
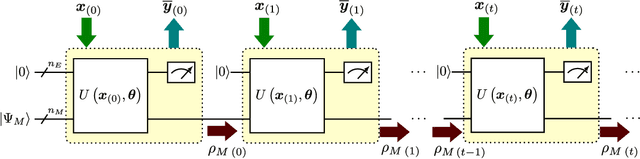
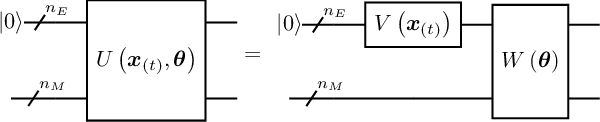
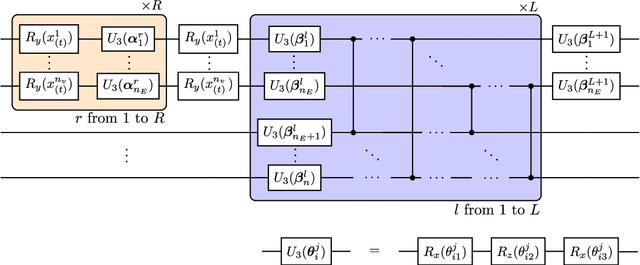
Quantum Recurrent Neural Networks (QRNNs) are robust candidates to model and predict future values in multivariate time series. However, the effective implementation of some QRNN models is limited by the need of mid-circuit measurements. Those increase the requirements for quantum hardware, which in the current NISQ era does not allow reliable computations. Emulation arises as the main near-term alternative to explore the potential of QRNNs, but existing quantum emulators are not dedicated to circuits with multiple intermediate measurements. In this context, we design a specific emulation method that relies on density matrix formalism. The mathematical development is explicitly provided as a compact formulation by using tensor notation. It allows us to show how the present and past information from a time series is transmitted through the circuit, and how to reduce the computational cost in every time step of the emulated network. In addition, we derive the analytical gradient and the Hessian of the network outputs with respect to its trainable parameters, with an eye on gradient-based training and noisy outputs that would appear when using real quantum processors. We finally test the presented methods using a novel hardware-efficient ansatz and three diverse datasets that include univariate and multivariate time series. Our results show how QRNNs can make accurate predictions of future values by capturing non-trivial patterns of input series with different complexities.

Learning Optimal Classification Trees Robust to Distribution Shifts

We consider the problem of learning classification trees that are robust to distribution shifts between training and testing/deployment data. This problem arises frequently in high stakes settings such as public health and social work where data is often collected using self-reported surveys which are highly sensitive to e.g., the framing of the questions, the time when and place where the survey is conducted, and the level of comfort the interviewee has in sharing information with the interviewer. We propose a method for learning optimal robust classification trees based on mixed-integer robust optimization technology. In particular, we demonstrate that the problem of learning an optimal robust tree can be cast as a single-stage mixed-integer robust optimization problem with a highly nonlinear and discontinuous objective. We reformulate this problem equivalently as a two-stage linear robust optimization problem for which we devise a tailored solution procedure based on constraint generation. We evaluate the performance of our approach on numerous publicly available datasets, and compare the performance to a regularized, non-robust optimal tree. We show an increase of up to 12.48% in worst-case accuracy and of up to 4.85% in average-case accuracy across several datasets and distribution shifts from using our robust solution in comparison to the non-robust one.

ODTlearn: A Package for Learning Optimal Decision Trees for Prediction and Prescription

ODTLearn is an open-source Python package that provides methods for learning optimal decision trees for high-stakes predictive and prescriptive tasks based on the mixed-integer optimization (MIO) framework proposed in Aghaei et al. (2019) and several of its extensions. The current version of the package provides implementations for learning optimal classification trees, optimal fair classification trees, optimal classification trees robust to distribution shifts, and optimal prescriptive trees from observational data. We have designed the package to be easy to maintain and extend as new optimal decision tree problem classes, reformulation strategies, and solution algorithms are introduced. To this end, the package follows object-oriented design principles and supports both commercial (Gurobi) and open source (COIN-OR branch and cut) solvers. The package documentation and an extensive user guide can be found at https://d3m-research-group.github.io/odtlearn/. Additionally, users can view the package source code and submit feature requests and bug reports by visiting https://github.com/D3M-Research-Group/odtlearn.

Outlier detection in regression: conic quadratic formulations

In many applications, when building linear regression models, it is important to account for the presence of outliers, i.e., corrupted input data points. Such problems can be formulated as mixed-integer optimization problems involving cubic terms, each given by the product of a binary variable and a quadratic term of the continuous variables. Existing approaches in the literature, typically relying on the linearization of the cubic terms using big-M constraints, suffer from weak relaxation and poor performance in practice. In this work we derive stronger second-order conic relaxations that do not involve big-M constraints. Our computational experiments indicate that the proposed formulations are several orders-of-magnitude faster than existing big-M formulations in the literature for this problem.

Gain Confidence, Reduce Disappointment: A New Approach to Cross-Validation for Sparse Regression

Ridge regularized sparse regression involves selecting a subset of features that explains the relationship between a design matrix and an output vector in an interpretable manner. To select the sparsity and robustness of linear regressors, techniques like leave-one-out cross-validation are commonly used for hyperparameter tuning. However, cross-validation typically increases the cost of sparse regression by several orders of magnitude. Additionally, validation metrics are noisy estimators of the test-set error, with different hyperparameter combinations giving models with different amounts of noise. Therefore, optimizing over these metrics is vulnerable to out-of-sample disappointment, especially in underdetermined settings. To address this, we make two contributions. First, we leverage the generalization theory literature to propose confidence-adjusted variants of leave-one-out that display less propensity to out-of-sample disappointment. Second, we leverage ideas from the mixed-integer literature to obtain computationally tractable relaxations of confidence-adjusted leave-one-out, thereby minimizing it without solving as many MIOs. Our relaxations give rise to an efficient coordinate descent scheme which allows us to obtain significantly lower leave-one-out errors than via other methods in the literature. We validate our theory by demonstrating we obtain significantly sparser and comparably accurate solutions than via popular methods like GLMNet and suffer from less out-of-sample disappointment. On synthetic datasets, our confidence adjustment procedure generates significantly fewer false discoveries, and improves out-of-sample performance by 2-5% compared to cross-validating without confidence adjustment. Across a suite of 13 real datasets, a calibrated version of our procedure improves the test set error by an average of 4% compared to cross-validating without confidence adjustment.

Learning Optimal Fair Classification Trees

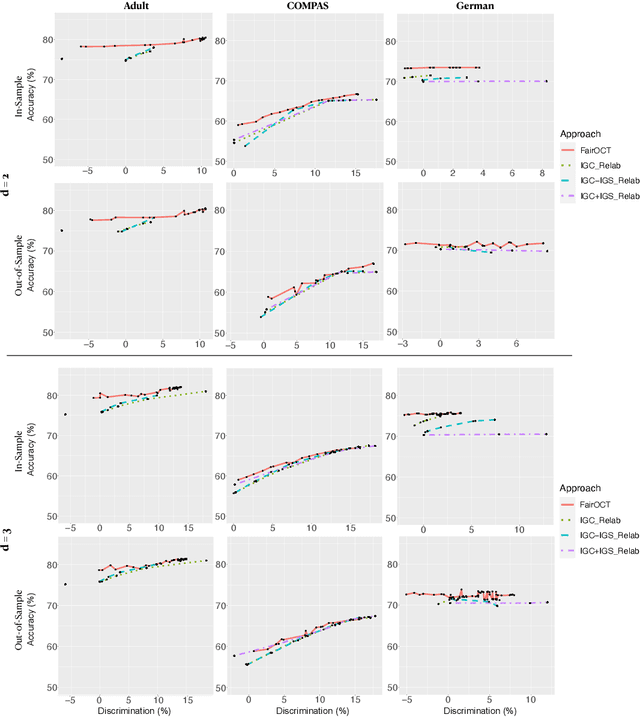
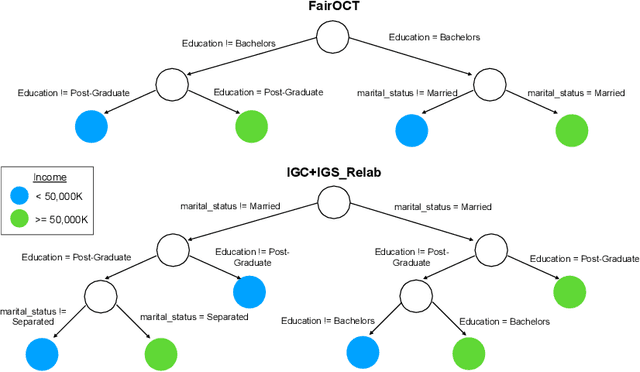
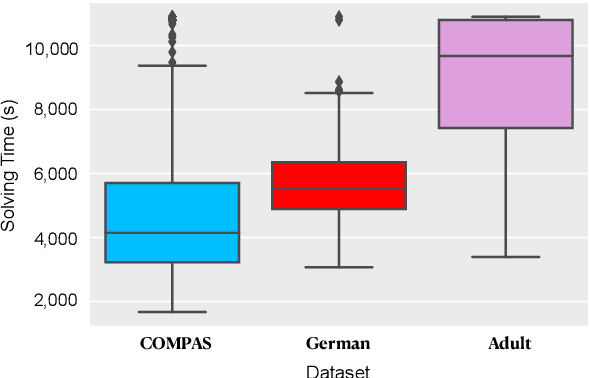
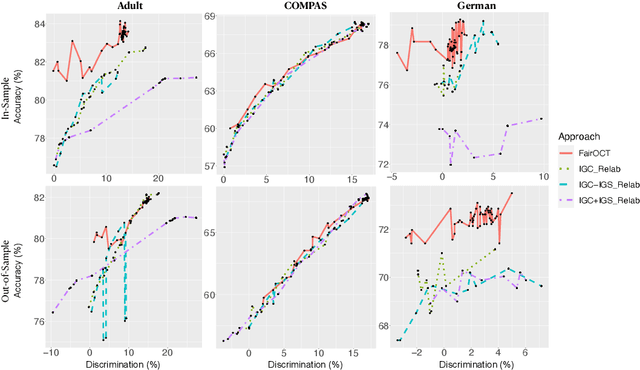
The increasing use of machine learning in high-stakes domains -- where people's livelihoods are impacted -- creates an urgent need for interpretable and fair algorithms. In these settings it is also critical for such algorithms to be accurate. With these needs in mind, we propose a mixed integer optimization (MIO) framework for learning optimal classification trees of fixed depth that can be conveniently augmented with arbitrary domain specific fairness constraints. We benchmark our method against the state-of-the-art approach for building fair trees on popular datasets; given a fixed discrimination threshold, our approach improves out-of-sample (OOS) accuracy by 2.3 percentage points on average and obtains a higher OOS accuracy on 88.9% of the experiments. We also incorporate various algorithmic fairness notions into our method, showcasing its versatile modeling power that allows decision makers to fine-tune the trade-off between accuracy and fairness.