Robust support vector machines via conic optimization

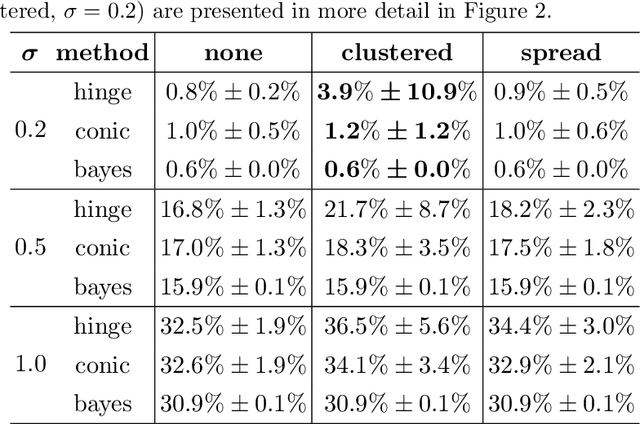
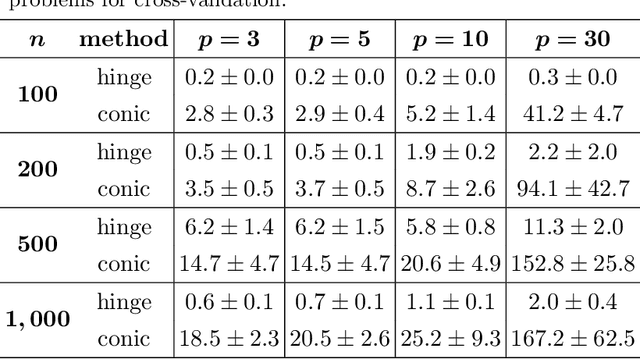
We consider the problem of learning support vector machines robust to uncertainty. It has been established in the literature that typical loss functions, including the hinge loss, are sensible to data perturbations and outliers, thus performing poorly in the setting considered. In contrast, using the 0-1 loss or a suitable non-convex approximation results in robust estimators, at the expense of large computational costs. In this paper we use mixed-integer optimization techniques to derive a new loss function that better approximates the 0-1 loss compared with existing alternatives, while preserving the convexity of the learning problem. In our computational results, we show that the proposed estimator is competitive with the standard SVMs with the hinge loss in outlier-free regimes and better in the presence of outliers.

Sparse and Smooth Signal Estimation: Convexification of L0 Formulations

Signal estimation problems with smoothness and sparsity priors can be naturally modeled as quadratic optimization with $\ell_0$-"norm" constraints. Since such problems are non-convex and hard-to-solve, the standard approach is, instead, to tackle their convex surrogates based on $\ell_1$-norm relaxations. In this paper, we propose new iterative conic quadratic relaxations that exploit not only the $\ell_0$-"norm" terms, but also the fitness and smoothness functions. The iterative convexification approach substantially closes the gap between the $\ell_0$-"norm" and its $\ell_1$ surrogate. Experiments using an off-the-shelf conic quadratic solver on synthetic as well as real datasets indicate that the proposed iterative convex relaxations lead to significantly better estimators than $\ell_1$-norm while preserving the computational efficiency. In addition, the parameters of the model and the resulting estimators are easily interpretable.