Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part II: Theoretical & Computational Results

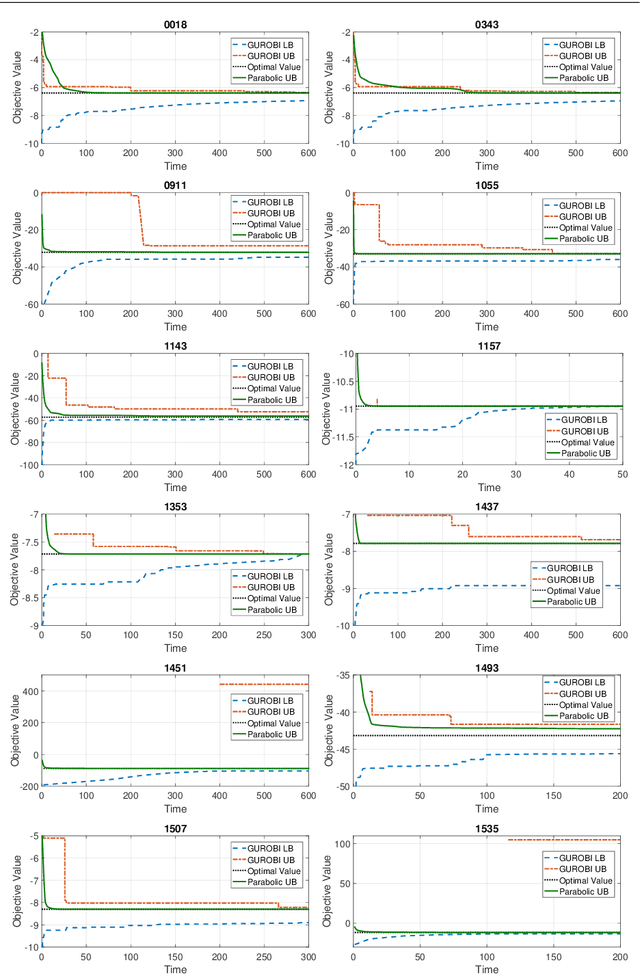
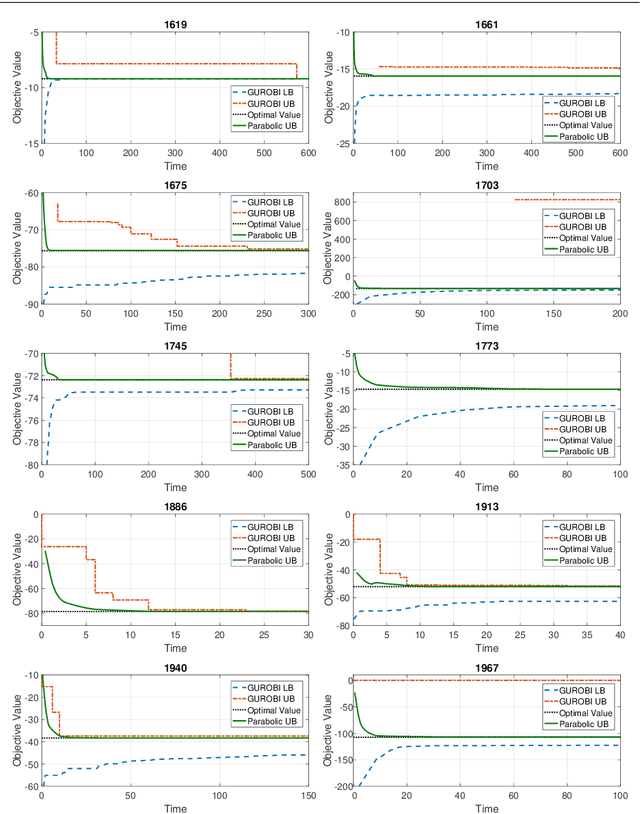
In the first part of this work [32], we introduce a convex parabolic relaxation for quadratically-constrained quadratic programs, along with a sequential penalized parabolic relaxation algorithm to recover near-optimal feasible solutions. In this second part, we show that starting from a feasible solution or a near-feasible solution satisfying certain regularity conditions, the sequential penalized parabolic relaxation algorithm convergences to a point which satisfies Karush-Kuhn-Tucker optimality conditions. Next, we present numerical experiments on benchmark non-convex QCQP problems as well as large-scale instances of system identification problem demonstrating the efficiency of the proposed approach.

Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part I: Definitions & Basic Properties

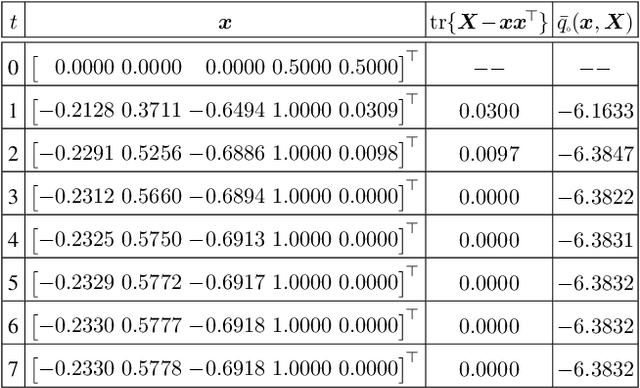
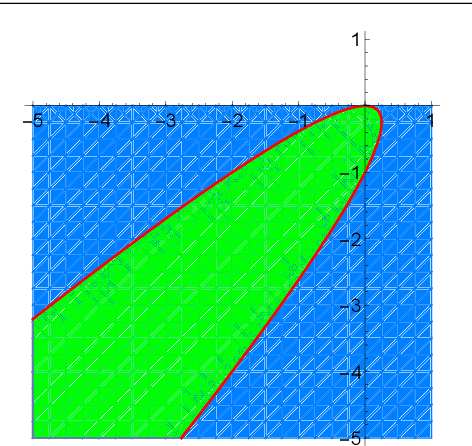
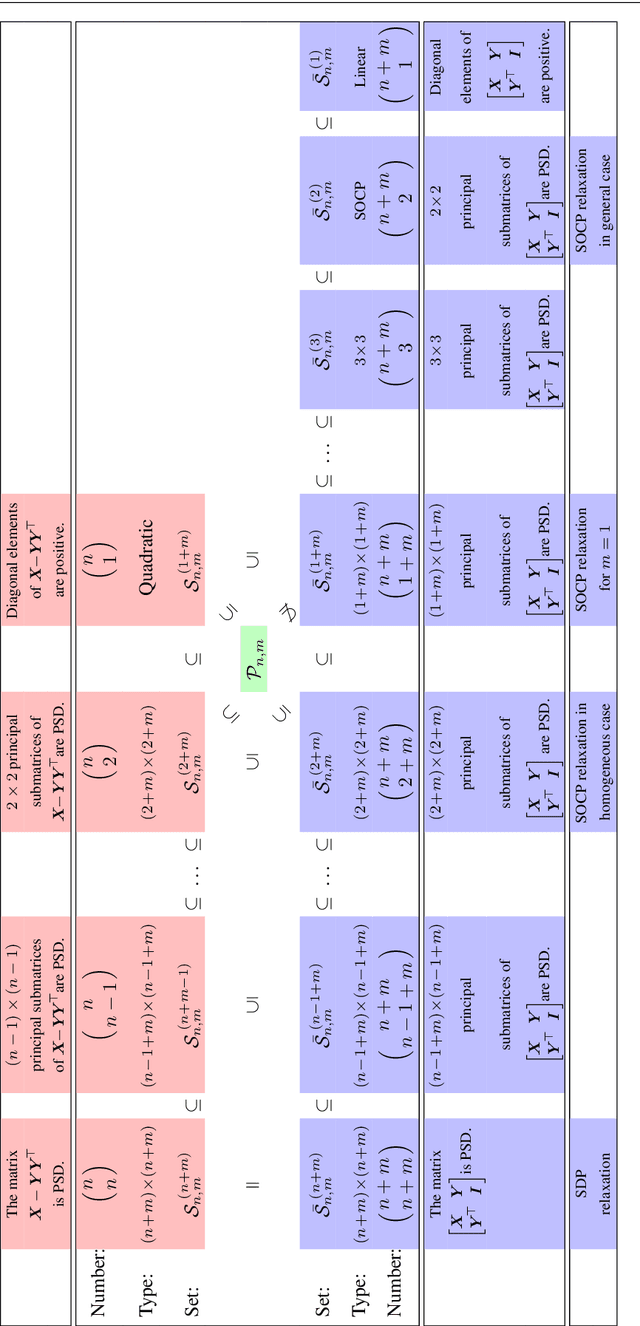
For general quadratically-constrained quadratic programming (QCQP), we propose a parabolic relaxation described with convex quadratic constraints. An interesting property of the parabolic relaxation is that the original non-convex feasible set is contained on the boundary of the parabolic relaxation. Under certain assumptions, this property enables one to recover near-optimal feasible points via objective penalization. Moreover, through an appropriate change of coordinates that requires a one-time computation of an optimal basis, the easier-to-solve parabolic relaxation can be made as strong as a semidefinite programming (SDP) relaxation, which can be effective in accelerating algorithms that require solving a sequence of convex surrogates. The majority of theoretical and computational results are given in the next part of this work [57].

Safe Screening for Logistic Regression with $\ell_0$-$\ell_2$ Regularization

In logistic regression, it is often desirable to utilize regularization to promote sparse solutions, particularly for problems with a large number of features compared to available labels. In this paper, we present screening rules that safely remove features from logistic regression with $\ell_0-\ell_2$ regularization before solving the problem. The proposed safe screening rules are based on lower bounds from the Fenchel dual of strong conic relaxations of the logistic regression problem. Numerical experiments with real and synthetic data suggest that a high percentage of the features can be effectively and safely removed apriori, leading to substantial speed-up in the computations.

Supermodularity and valid inequalities for quadratic optimization with indicators

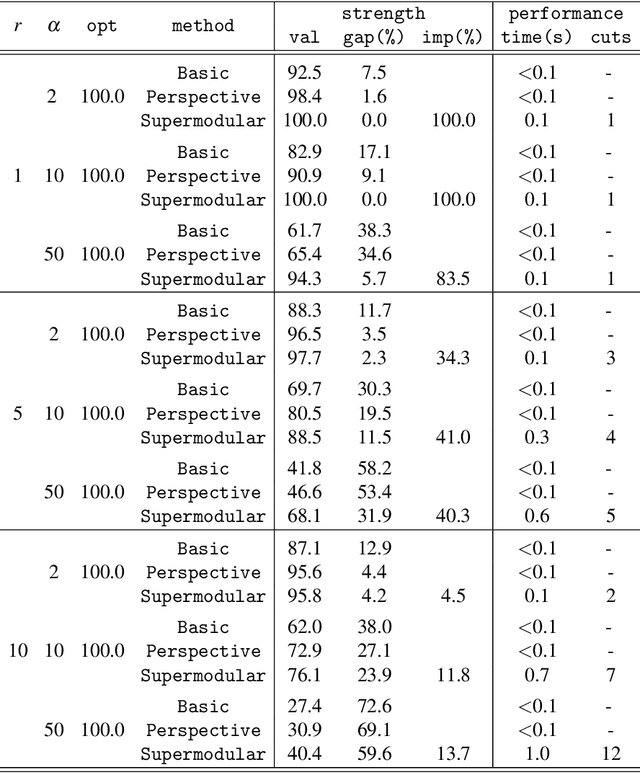
We study the minimization of a rank-one quadratic with indicators and show that the underlying set function obtained by projecting out the continuous variables is supermodular. Although supermodular minimization is, in general, difficult, the specific set function for the rank-one quadratic can be minimized in linear time. We show that the convex hull of the epigraph of the quadratic can be obtaining from inequalities for the underlying supermodular set function by lifting them into nonlinear inequalities in the original space of variables. Explicit forms of the convex-hull description are given, both in the original space of variables and in an extended formulation via conic quadratic-representable inequalities, along with a polynomial separation algorithm. Computational experiments indicate that the lifted supermodular inequalities in conic quadratic form are quite effective in reducing the integrality gap for quadratic optimization with indicators.

Submodular Function Minimization and Polarity

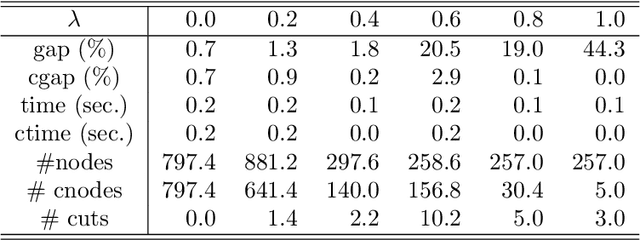
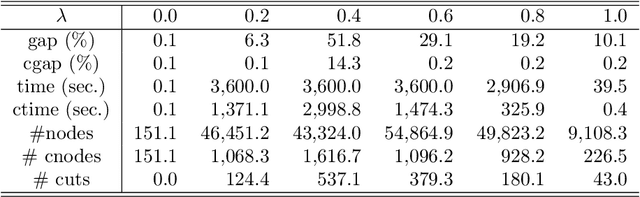
Using polarity, we give an outer polyhedral approximation for the epigraph of set functions. For a submodular function, we prove that the corresponding polar relaxation is exact; hence, it is equivalent to the Lov\'asz extension. The polar approach provides an alternative proof for the convex hull description of the epigraph of a submodular function. Computational experiments show that the inequalities from outer approximations can be effective as cutting planes for solving submodular as well as non-submodular set function minimization problems.

Rank-one Convexification for Sparse Regression

Sparse regression models are increasingly prevalent due to their ease of interpretability and superior out-of-sample performance. However, the exact model of sparse regression with an $\ell_0$ constraint restricting the support of the estimators is a challenging non-convex optimization problem. In this paper, we derive new strong convex relaxations for sparse regression. These relaxations are based on the ideal (convex-hull) formulations for rank-one quadratic terms with indicator variables. The new relaxations can be formulated as semidefinite optimization problems in an extended space and are stronger and more general than the state-of-the-art formulations, including the perspective reformulation and formulations with the reverse Huber penalty and the minimax concave penalty functions. Furthermore, the proposed rank-one strengthening can be interpreted as a non-separable, non-convex sparsity-inducing regularizer, which dynamically adjusts its penalty according to the shape of the error function. In our computational experiments with benchmark datasets, the proposed conic formulations are solved within seconds and result in near-optimal solutions (with 0.4\% optimality gap) for non-convex $\ell_0$-problems. Moreover, the resulting estimators also outperform alternative convex approaches from a statistical viewpoint, achieving high prediction accuracy and good interpretability.

Sparse and Smooth Signal Estimation: Convexification of L0 Formulations

Signal estimation problems with smoothness and sparsity priors can be naturally modeled as quadratic optimization with $\ell_0$-"norm" constraints. Since such problems are non-convex and hard-to-solve, the standard approach is, instead, to tackle their convex surrogates based on $\ell_1$-norm relaxations. In this paper, we propose new iterative conic quadratic relaxations that exploit not only the $\ell_0$-"norm" terms, but also the fitness and smoothness functions. The iterative convexification approach substantially closes the gap between the $\ell_0$-"norm" and its $\ell_1$ surrogate. Experiments using an off-the-shelf conic quadratic solver on synthetic as well as real datasets indicate that the proposed iterative convex relaxations lead to significantly better estimators than $\ell_1$-norm while preserving the computational efficiency. In addition, the parameters of the model and the resulting estimators are easily interpretable.