Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part II: Theoretical & Computational Results

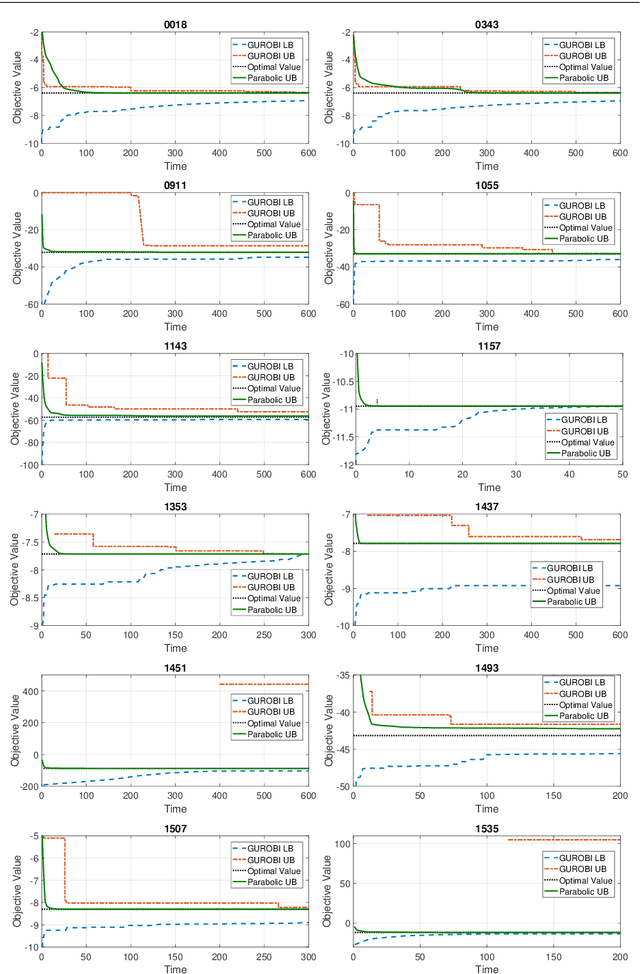
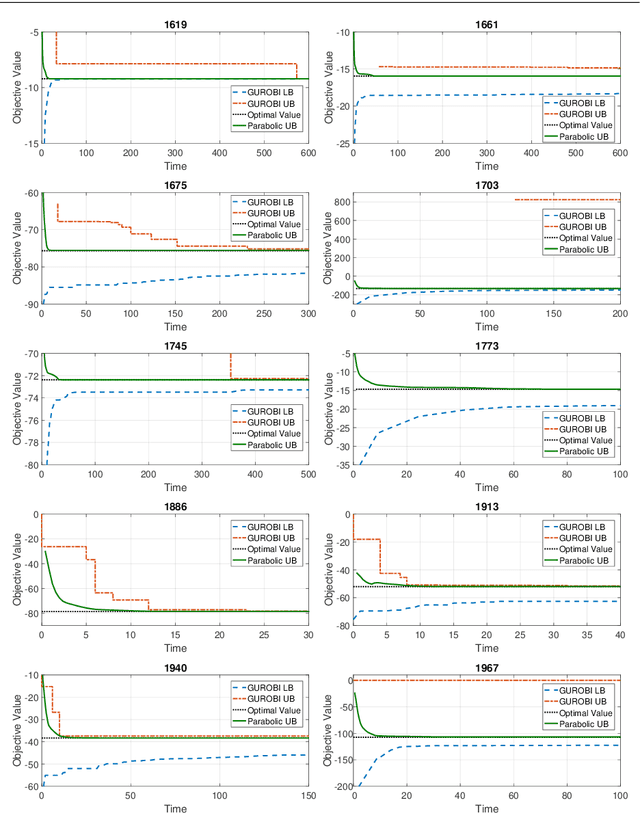
In the first part of this work [32], we introduce a convex parabolic relaxation for quadratically-constrained quadratic programs, along with a sequential penalized parabolic relaxation algorithm to recover near-optimal feasible solutions. In this second part, we show that starting from a feasible solution or a near-feasible solution satisfying certain regularity conditions, the sequential penalized parabolic relaxation algorithm convergences to a point which satisfies Karush-Kuhn-Tucker optimality conditions. Next, we present numerical experiments on benchmark non-convex QCQP problems as well as large-scale instances of system identification problem demonstrating the efficiency of the proposed approach.

Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part I: Definitions & Basic Properties

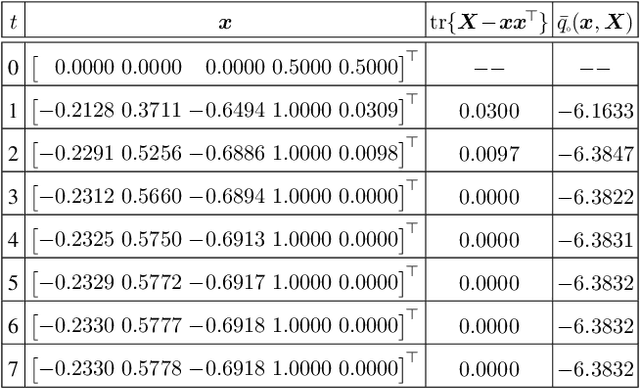
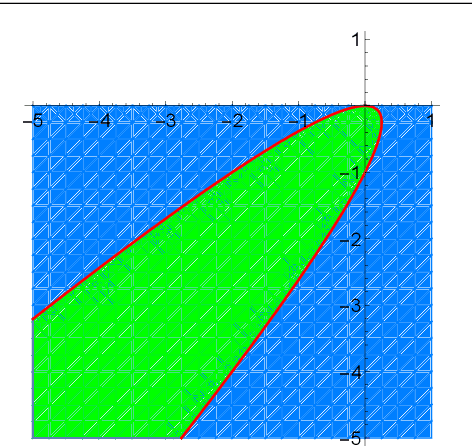
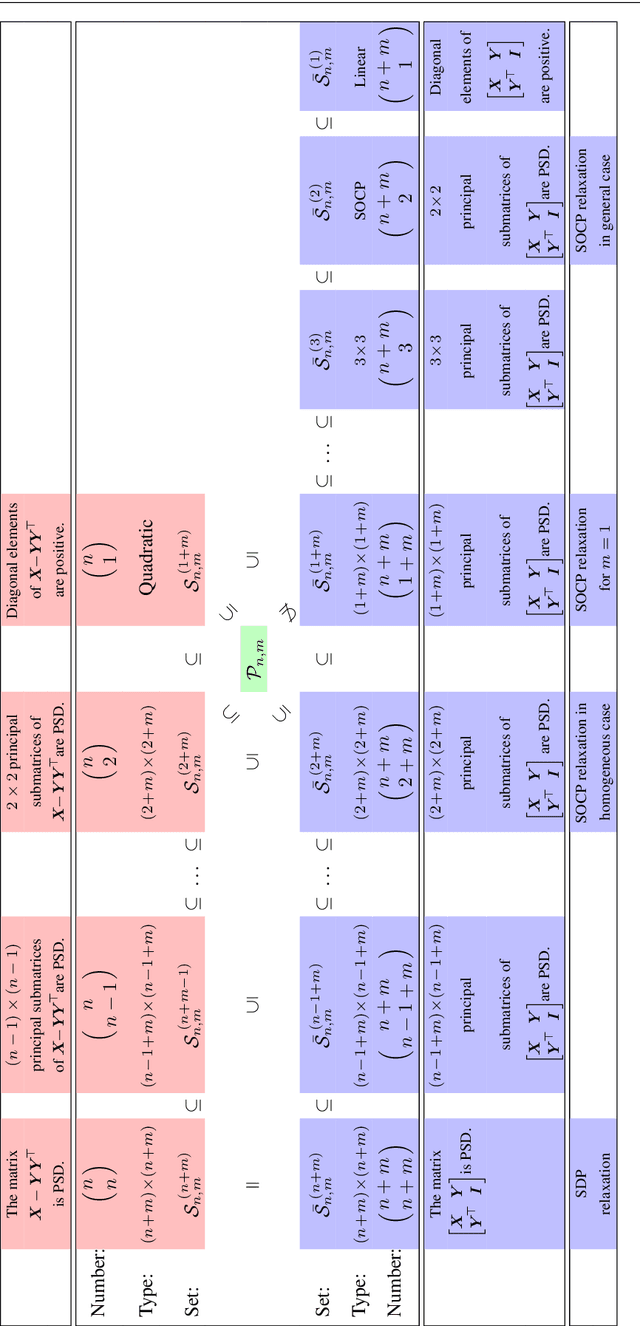
For general quadratically-constrained quadratic programming (QCQP), we propose a parabolic relaxation described with convex quadratic constraints. An interesting property of the parabolic relaxation is that the original non-convex feasible set is contained on the boundary of the parabolic relaxation. Under certain assumptions, this property enables one to recover near-optimal feasible points via objective penalization. Moreover, through an appropriate change of coordinates that requires a one-time computation of an optimal basis, the easier-to-solve parabolic relaxation can be made as strong as a semidefinite programming (SDP) relaxation, which can be effective in accelerating algorithms that require solving a sequence of convex surrogates. The majority of theoretical and computational results are given in the next part of this work [57].

Machine Learning Based Relative Orbit Transfer for Swarm Spacecraft Motion Planning

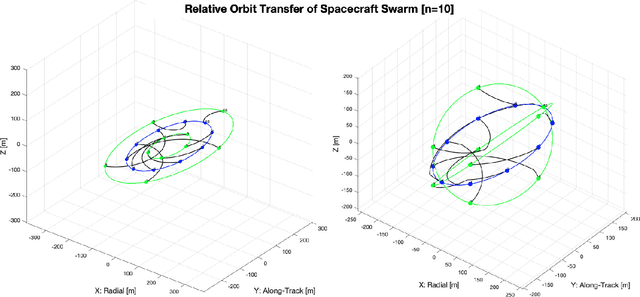
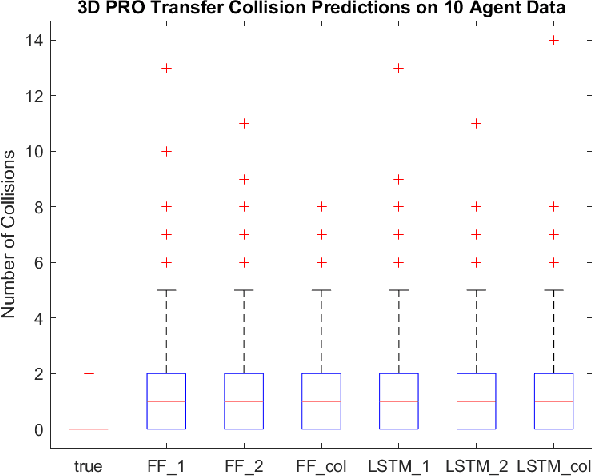
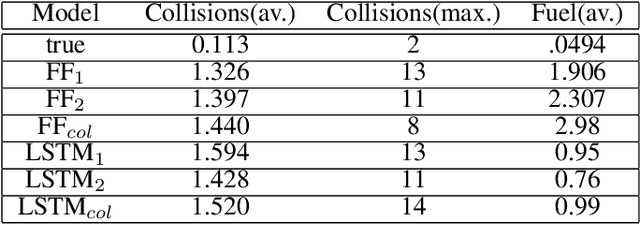
In this paper we describe a machine learning based framework for spacecraft swarm trajectory planning. In particular, we focus on coordinating motions of multi-spacecraft in formation flying through passive relative orbit(PRO) transfers. Accounting for spacecraft dynamics while avoiding collisions between the agents makes spacecraft swarm trajectory planning difficult. Centralized approaches can be used to solve this problem, but are computationally demanding and scale poorly with the number of agents in the swarm. As a result, centralized algorithms are ill-suited for real time trajectory planning on board small spacecraft (e.g. CubeSats) comprising the swarm. In our approach a neural network is used to approximate solutions of a centralized method. The necessary training data is generated using a centralized convex optimization framework through which several instances of the n=10 spacecraft swarm trajectory planning problem are solved. We are interested in answering the following questions which will give insight on the potential utility of deep learning-based approaches to the multi-spacecraft motion planning problem: 1) Can neural networks produce feasible trajectories that satisfy safety constraints (e.g. collision avoidance) and low in fuel cost? 2) Can a neural network trained using n spacecraft data be used to solve problems for spacecraft swarms of differing size?

Optimal Multi-Robot Motion Planning via Parabolic Relaxation

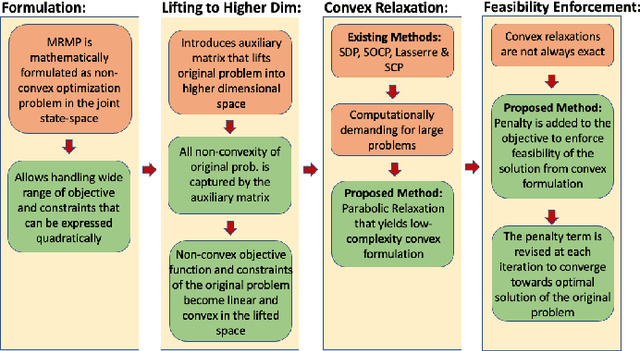
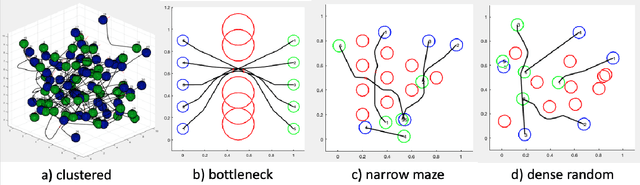
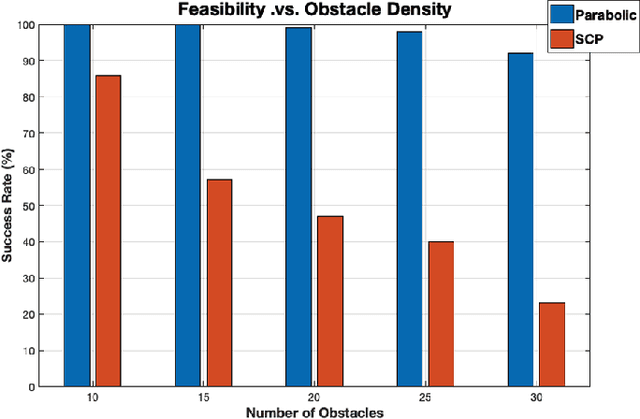
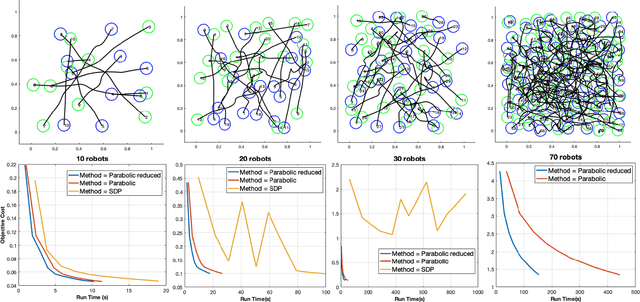
Multi-robot systems offer enhanced capability over their monolithic counterparts, but they come at a cost of increased complexity in coordination. To reduce complexity and to make the problem tractable, multi-robot motion planning (MRMP) methods in the literature adopt de-coupled approaches that sacrifice either optimality or dynamic feasibility. In this paper, we present a convexification method, namely "parabolic relaxation", to generate optimal and dynamically feasible trajectories for MRMP in the coupled joint-space of all robots. We leverage upon the proposed relaxation to tackle the problem complexity and to attain computational tractability for planning over one hundred robots in extremely clustered environments. We take a multi-stage optimization approach that consists of i) mathematically formulating MRMP as a non-convex optimization, ii) lifting the problem into a higher dimensional space, iii) convexifying the problem through the proposed computationally efficient parabolic relaxation, and iv) penalizing with iterative search to ensure feasibility and recovery of feasible and near-optimal solutions to the original problem. Our numerical experiments demonstrate that the proposed approach is capable of generating optimal and dynamically feasible trajectories for challenging motion planning problems with higher success rate than the state-of-the-art, yet remain computationally tractable for over one hundred robots in a highly dense environment.

Multi-Agent Motion Planning using Deep Learning for Space Applications

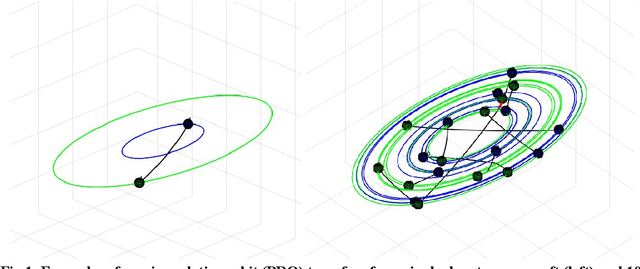
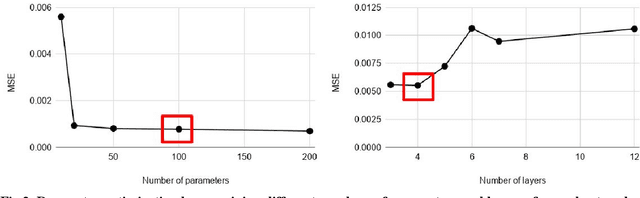
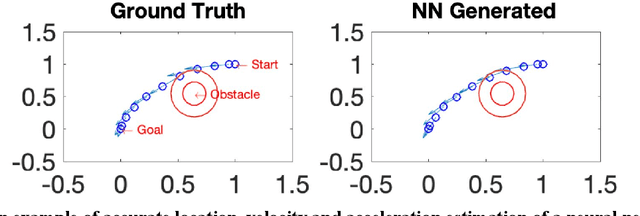
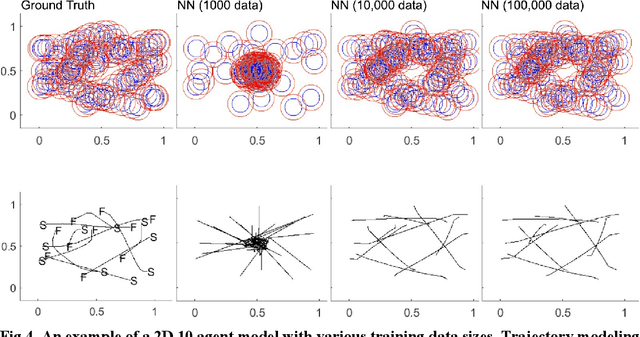
State-of-the-art motion planners cannot scale to a large number of systems. Motion planning for multiple agents is an NP (non-deterministic polynomial-time) hard problem, so the computation time increases exponentially with each addition of agents. This computational demand is a major stumbling block to the motion planner's application to future NASA missions involving the swarm of space vehicles. We applied a deep neural network to transform computationally demanding mathematical motion planning problems into deep learning-based numerical problems. We showed optimal motion trajectories can be accurately replicated using deep learning-based numerical models in several 2D and 3D systems with multiple agents. The deep learning-based numerical model demonstrates superior computational efficiency with plans generated 1000 times faster than the mathematical model counterpart.