Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part II: Theoretical & Computational Results

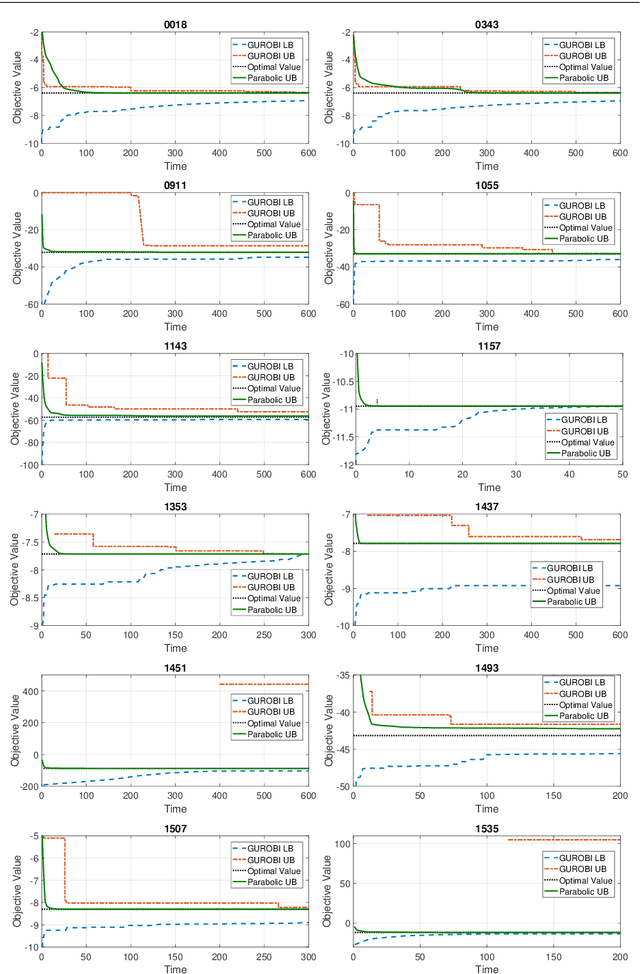
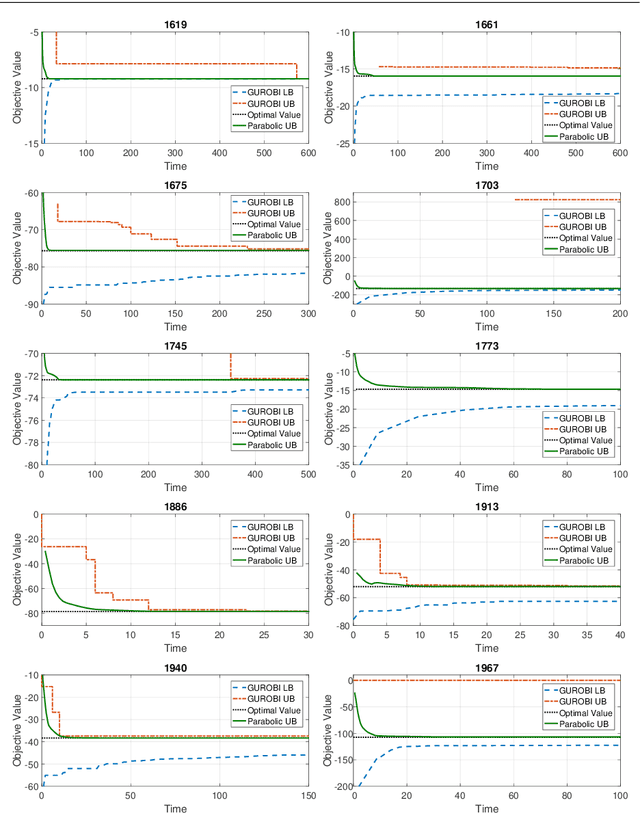
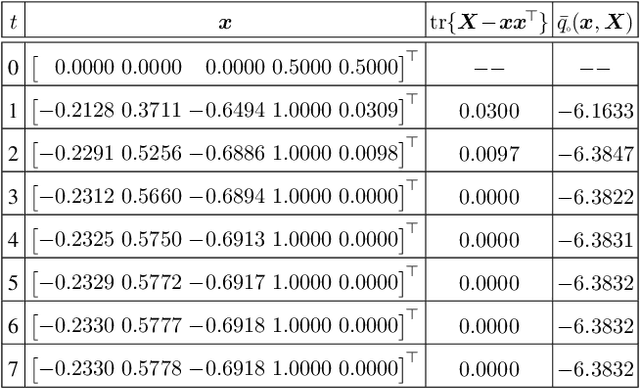
In the first part of this work [32], we introduce a convex parabolic relaxation for quadratically-constrained quadratic programs, along with a sequential penalized parabolic relaxation algorithm to recover near-optimal feasible solutions. In this second part, we show that starting from a feasible solution or a near-feasible solution satisfying certain regularity conditions, the sequential penalized parabolic relaxation algorithm convergences to a point which satisfies Karush-Kuhn-Tucker optimality conditions. Next, we present numerical experiments on benchmark non-convex QCQP problems as well as large-scale instances of system identification problem demonstrating the efficiency of the proposed approach.

Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part I: Definitions & Basic Properties

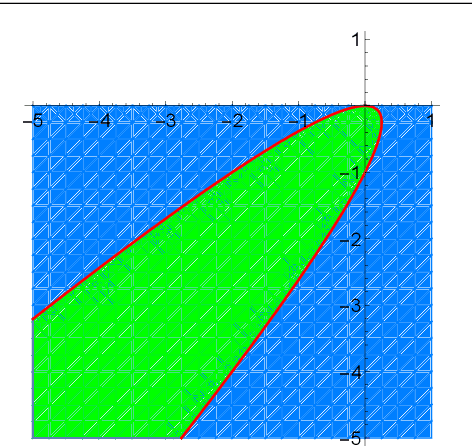
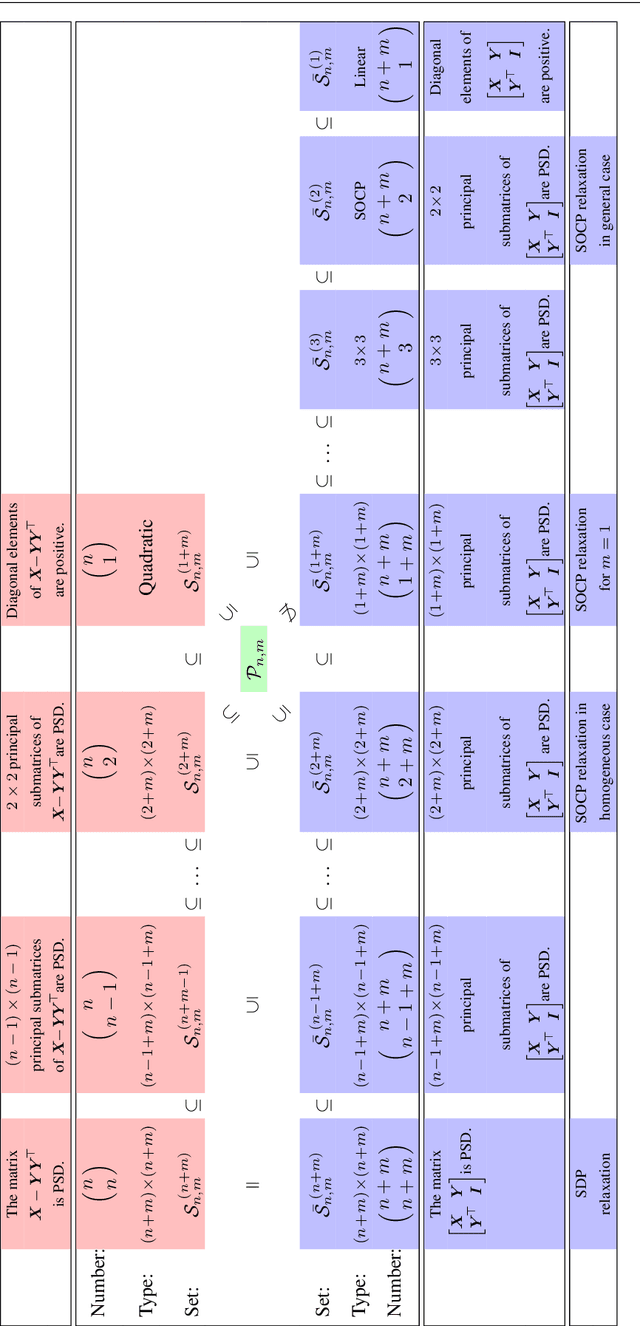
For general quadratically-constrained quadratic programming (QCQP), we propose a parabolic relaxation described with convex quadratic constraints. An interesting property of the parabolic relaxation is that the original non-convex feasible set is contained on the boundary of the parabolic relaxation. Under certain assumptions, this property enables one to recover near-optimal feasible points via objective penalization. Moreover, through an appropriate change of coordinates that requires a one-time computation of an optimal basis, the easier-to-solve parabolic relaxation can be made as strong as a semidefinite programming (SDP) relaxation, which can be effective in accelerating algorithms that require solving a sequence of convex surrogates. The majority of theoretical and computational results are given in the next part of this work [57].