Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part II: Theoretical & Computational Results

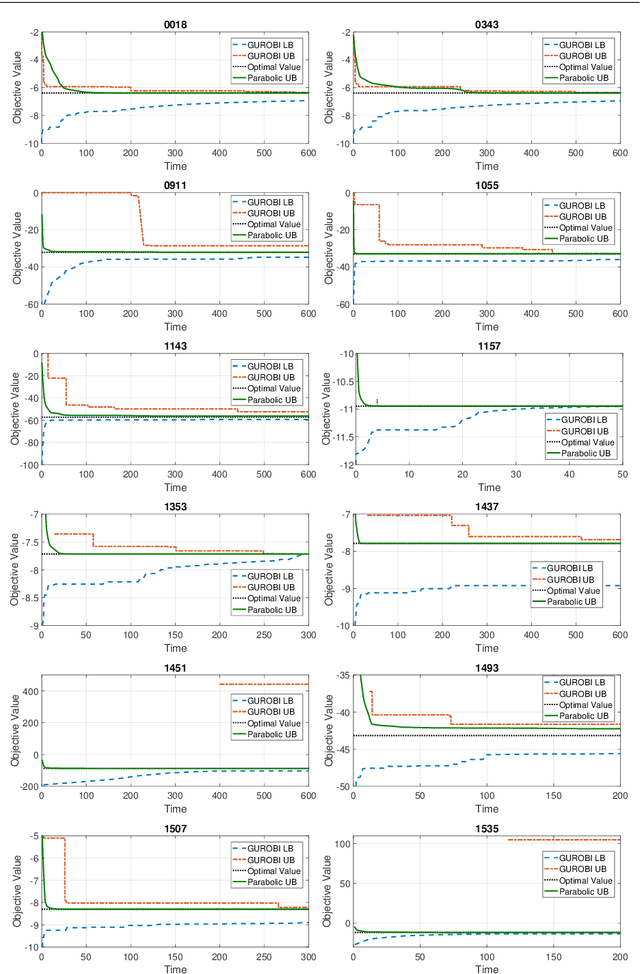
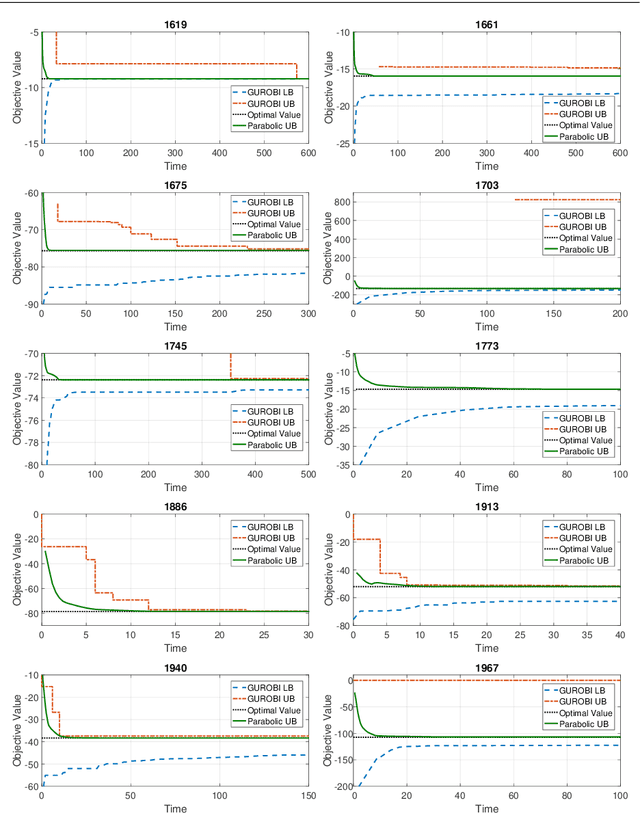
In the first part of this work [32], we introduce a convex parabolic relaxation for quadratically-constrained quadratic programs, along with a sequential penalized parabolic relaxation algorithm to recover near-optimal feasible solutions. In this second part, we show that starting from a feasible solution or a near-feasible solution satisfying certain regularity conditions, the sequential penalized parabolic relaxation algorithm convergences to a point which satisfies Karush-Kuhn-Tucker optimality conditions. Next, we present numerical experiments on benchmark non-convex QCQP problems as well as large-scale instances of system identification problem demonstrating the efficiency of the proposed approach.

Parabolic Relaxation for Quadratically-constrained Quadratic Programming -- Part I: Definitions & Basic Properties

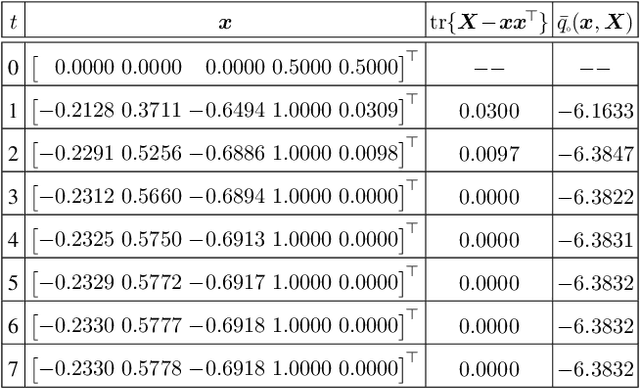
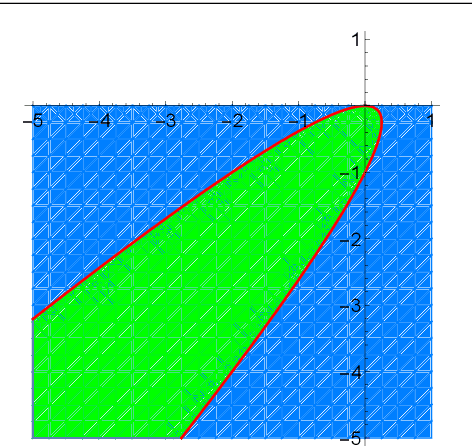
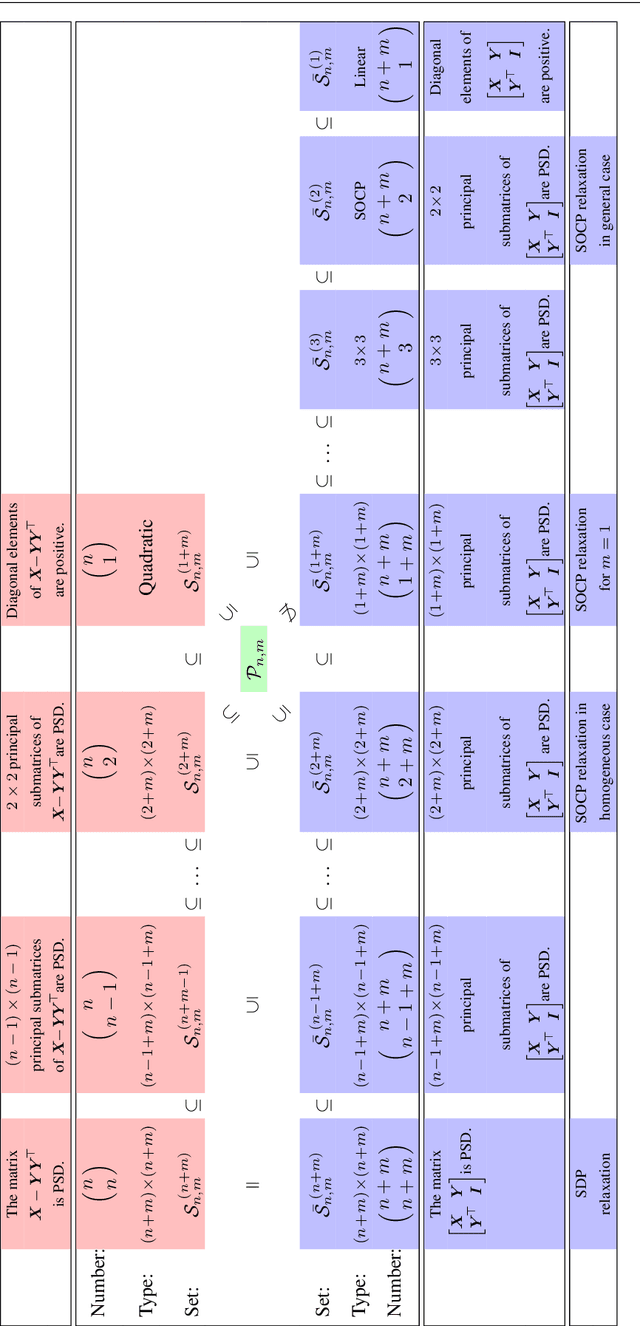
For general quadratically-constrained quadratic programming (QCQP), we propose a parabolic relaxation described with convex quadratic constraints. An interesting property of the parabolic relaxation is that the original non-convex feasible set is contained on the boundary of the parabolic relaxation. Under certain assumptions, this property enables one to recover near-optimal feasible points via objective penalization. Moreover, through an appropriate change of coordinates that requires a one-time computation of an optimal basis, the easier-to-solve parabolic relaxation can be made as strong as a semidefinite programming (SDP) relaxation, which can be effective in accelerating algorithms that require solving a sequence of convex surrogates. The majority of theoretical and computational results are given in the next part of this work [57].

Class Conditional Alignment for Partial Domain Adaptation

Adversarial adaptation models have demonstrated significant progress towards transferring knowledge from a labeled source dataset to an unlabeled target dataset. Partial domain adaptation (PDA) investigates the scenarios in which the source domain is large and diverse, and the target label space is a subset of the source label space. The main purpose of PDA is to identify the shared classes between the domains and promote learning transferable knowledge from these classes. In this paper, we propose a multi-class adversarial architecture for PDA. The proposed approach jointly aligns the marginal and class-conditional distributions in the shared label space by minimaxing a novel multi-class adversarial loss function. Furthermore, we incorporate effective regularization terms to encourage selecting the most relevant subset of source domain classes. In the absence of target labels, the proposed approach is able to effectively learn domain-invariant feature representations, which in turn can enhance the classification performance in the target domain. Comprehensive experiments on three benchmark datasets Office-31, Office-Home, and Caltech-Office corroborate the effectiveness of the proposed approach in addressing different partial transfer learning tasks.

Multi-Level Representation Learning for Deep Subspace Clustering

This paper proposes a novel deep subspace clustering approach which uses convolutional autoencoders to transform input images into new representations lying on a union of linear subspaces. The first contribution of our work is to insert multiple fully-connected linear layers between the encoder layers and their corresponding decoder layers to promote learning more favorable representations for subspace clustering. These connection layers facilitate the feature learning procedure by combining low-level and high-level information for generating multiple sets of self-expressive and informative representations at different levels of the encoder. Moreover, we introduce a novel loss minimization problem which leverages an initial clustering of the samples to effectively fuse the multi-level representations and recover the underlying subspaces more accurately. The loss function is then minimized through an iterative scheme which alternatively updates the network parameters and produces new clusterings of the samples. Experiments on four real-world datasets demonstrate that our approach exhibits superior performance compared to the state-of-the-art methods on most of the subspace clustering problems.

Image Segmentation using Sparse Subset Selection

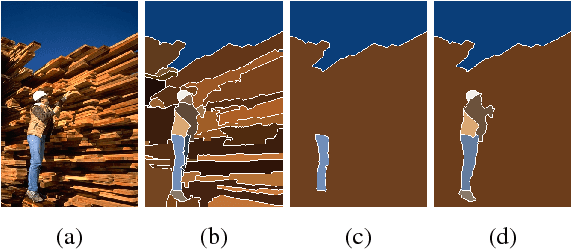
In this paper, we present a new image segmentation method based on the concept of sparse subset selection. Starting with an over-segmentation, we adopt local spectral histogram features to encode the visual information of the small segments into high-dimensional vectors, called superpixel features. Then, the superpixel features are fed into a novel convex model which efficiently leverages the features to group the superpixels into a proper number of coherent regions. Our model automatically determines the optimal number of coherent regions and superpixels assignment to shape final segments. To solve our model, we propose a numerical algorithm based on the alternating direction method of multipliers (ADMM), whose iterations consist of two highly parallelizable sub-problems. We show each sub-problem enjoys closed-form solution which makes the ADMM iterations computationally very efficient. Extensive experiments on benchmark image segmentation datasets demonstrate that our proposed method in combination with an over-segmentation can provide high quality and competitive results compared to the existing state-of-the-art methods.

Natural Scene Image Segmentation Based on Multi-Layer Feature Extraction

This paper addresses the problem of natural image segmentation by extracting information from a multi-layer array which is constructed based on color, gradient, and statistical properties of the local neighborhoods in an image. A Gaussian Mixture Model (GMM) is used to improve the effectiveness of local spectral histogram features. Grouping these features leads to forming a rough initial over-segmented layer which contains coherent regions of pixels. The regions are merged by using two proposed functions for calculating the distance between two neighboring regions and making decisions about their merging. Extensive experiments are performed on the Berkeley Segmentation Dataset to evaluate the performance of our proposed method and compare the results with the recent state-of-the-art methods. The experimental results indicate that our method achieves higher level of accuracy for natural images compared to recent methods.