Fair and Accurate Regression: Strong Formulations and Algorithms

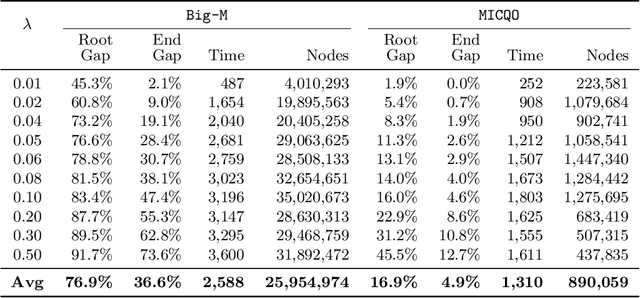
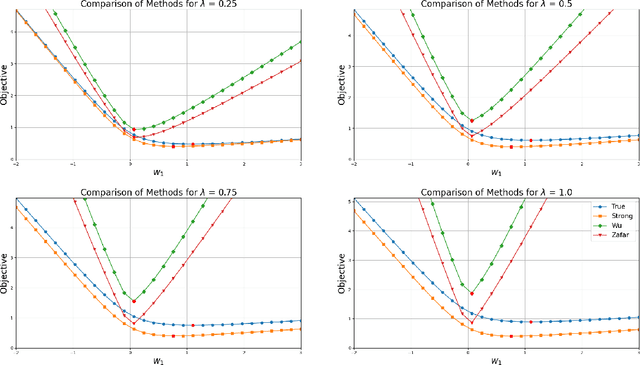
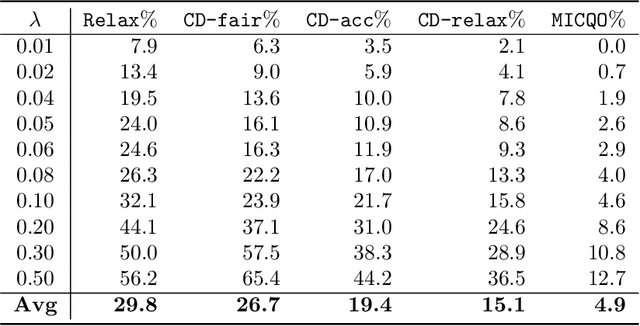
This paper introduces mixed-integer optimization methods to solve regression problems that incorporate fairness metrics. We propose an exact formulation for training fair regression models. To tackle this computationally hard problem, we study the polynomially-solvable single-factor and single-observation subproblems as building blocks and derive their closed convex hull descriptions. Strong formulations obtained for the general fair regression problem in this manner are utilized to solve the problem with a branch-and-bound algorithm exactly or as a relaxation to produce fair and accurate models rapidly. Moreover, to handle large-scale instances, we develop a coordinate descent algorithm motivated by the convex-hull representation of the single-factor fair regression problem to improve a given solution efficiently. Numerical experiments conducted on fair least squares and fair logistic regression problems show competitive statistical performance with state-of-the-art methods while significantly reducing training times.

Safe Screening for Logistic Regression with $\ell_0$-$\ell_2$ Regularization

In logistic regression, it is often desirable to utilize regularization to promote sparse solutions, particularly for problems with a large number of features compared to available labels. In this paper, we present screening rules that safely remove features from logistic regression with $\ell_0-\ell_2$ regularization before solving the problem. The proposed safe screening rules are based on lower bounds from the Fenchel dual of strong conic relaxations of the logistic regression problem. Numerical experiments with real and synthetic data suggest that a high percentage of the features can be effectively and safely removed apriori, leading to substantial speed-up in the computations.