Switch and Conquer: Efficient Algorithms By Switching Stochastic Gradient Oracles For Decentralized Saddle Point Problems

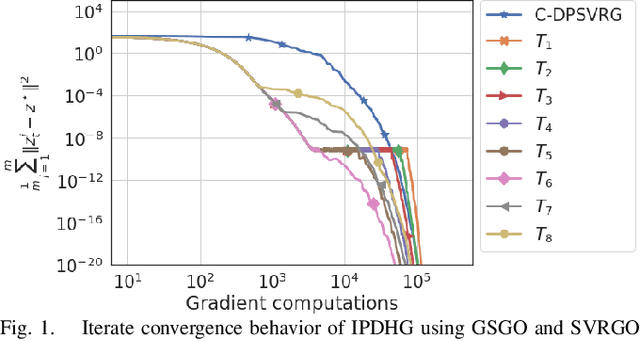
We consider a class of non-smooth strongly convex-strongly concave saddle point problems in a decentralized setting without a central server. To solve a consensus formulation of problems in this class, we develop an inexact primal dual hybrid gradient (inexact PDHG) procedure that allows generic gradient computation oracles to update the primal and dual variables. We first investigate the performance of inexact PDHG with stochastic variance reduction gradient (SVRG) oracle. Our numerical study uncovers a significant phenomenon of initial conservative progress of iterates of IPDHG with SVRG oracle. To tackle this, we develop a simple and effective switching idea, where a generalized stochastic gradient (GSG) computation oracle is employed to hasten the iterates' progress to a saddle point solution during the initial phase of updates, followed by a switch to the SVRG oracle at an appropriate juncture. The proposed algorithm is named Decentralized Proximal Switching Stochastic Gradient method with Compression (C-DPSSG), and is proven to converge to an $\epsilon$-accurate saddle point solution with linear rate. Apart from delivering highly accurate solutions, our study reveals that utilizing the best convergence phases of GSG and SVRG oracles makes C-DPSSG well suited for obtaining solutions of low/medium accuracy faster, useful for certain applications. Numerical experiments on two benchmark machine learning applications show C-DPSSG's competitive performance which validate our theoretical findings. The codes used in the experiments can be found \href{https://github.com/chhavisharma123/C-DPSSG-CDC2023}{here}.

Stochastic Gradient Methods with Compressed Communication for Decentralized Saddle Point Problems

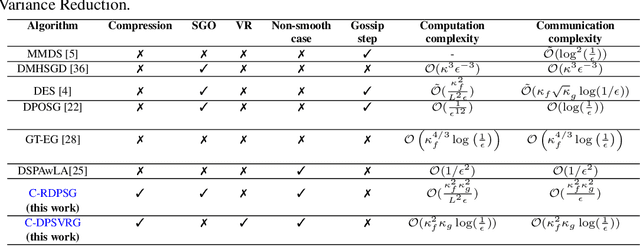
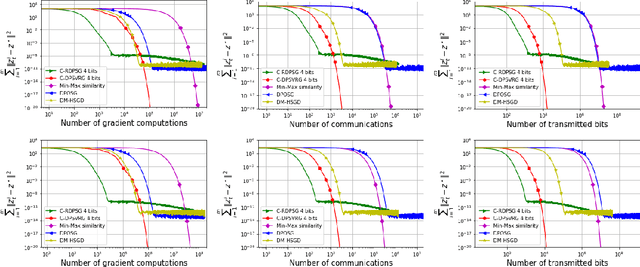
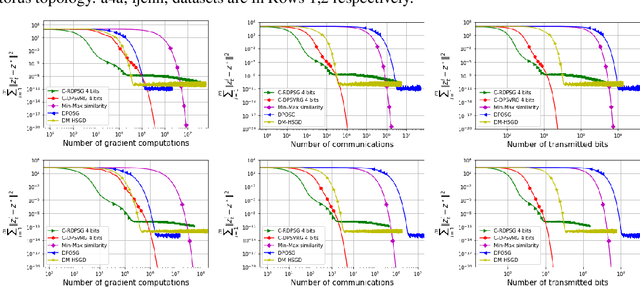
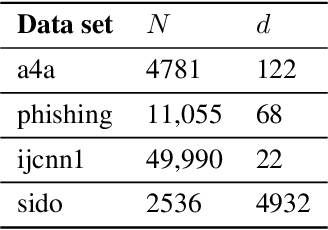
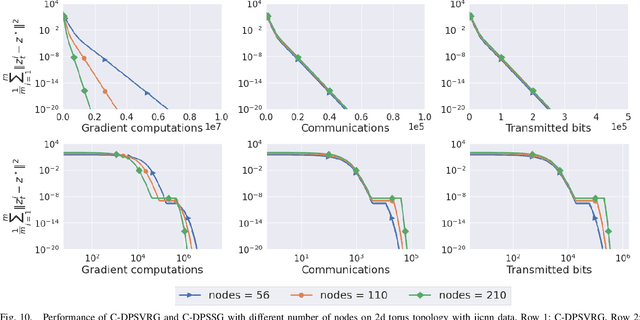
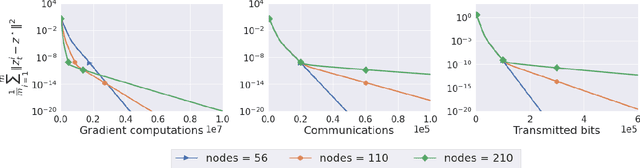
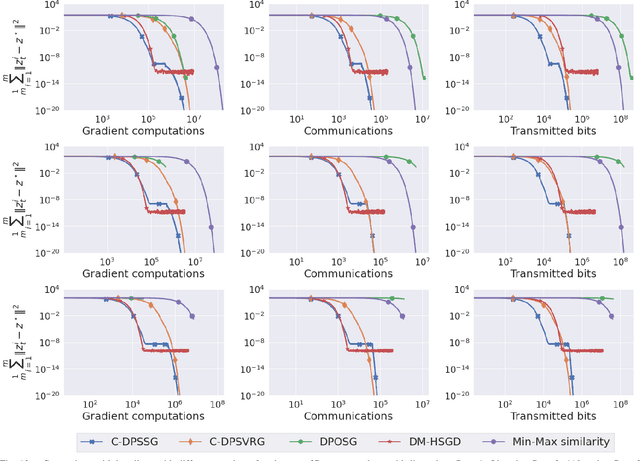
We propose two stochastic gradient algorithms to solve a class of saddle-point problems in a decentralized setting (without a central server). The proposed algorithms are the first to achieve sub-linear/linear computation and communication complexities using respectively stochastic gradient/stochastic variance reduced gradient oracles with compressed information exchange to solve non-smooth strongly-convex strongly-concave saddle-point problems in decentralized setting. Our first algorithm is a Restart-based Decentralized Proximal Stochastic Gradient method with Compression (C-RDPSG) for general stochastic settings. We provide rigorous theoretical guarantees of C-RDPSG with gradient computation complexity and communication complexity of order $\mathcal{O}( (1+\delta)^4 \frac{1}{L^2}{\kappa_f^2}\kappa_g^2 \frac{1}{\epsilon} )$, to achieve an $\epsilon$-accurate saddle-point solution, where $\delta$ denotes the compression factor, $\kappa_f$ and $\kappa_g$ denote respectively the condition numbers of objective function and communication graph, and $L$ denotes the smoothness parameter of the smooth part of the objective function. Next, we present a Decentralized Proximal Stochastic Variance Reduced Gradient algorithm with Compression (C-DPSVRG) for finite sum setting which exhibits gradient computation complexity and communication complexity of order $\mathcal{O}((1+\delta)\kappa_f^2 \kappa_g \log(\frac{1}{\epsilon}))$. Extensive numerical experiments show competitive performance of the proposed algorithms and provide support to the theoretical results obtained.

Submodular Function Minimization and Polarity

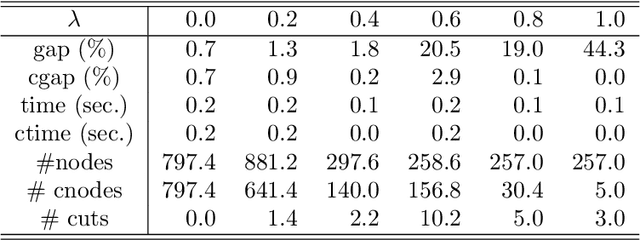
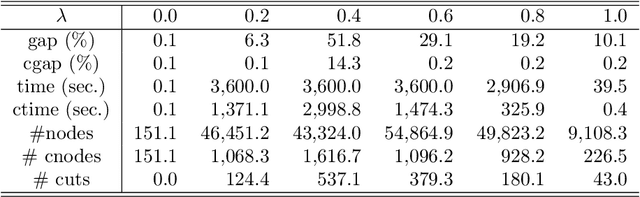
Using polarity, we give an outer polyhedral approximation for the epigraph of set functions. For a submodular function, we prove that the corresponding polar relaxation is exact; hence, it is equivalent to the Lov\'asz extension. The polar approach provides an alternative proof for the convex hull description of the epigraph of a submodular function. Computational experiments show that the inequalities from outer approximations can be effective as cutting planes for solving submodular as well as non-submodular set function minimization problems.